第一版
第二版
统计学习的主要特点是 :
统计学习以计算机及网络为平台,是建立在计算机及网络之上的;
统计学习以数据为研究对象,是数据驱动的学科;
统计学习的目的是对数据进行预测与分析;
统计学习以方法为中心,统计学习方法构建模型并应用模型进行预测与分析;
统计学习是概率论、统计学、信息论、计算理论、最优化理论及计算机科学等多个领域的交叉学科,并且在发展中逐步形成独自的理论体系与方法论。
假设空间(hypothesis space) :H = { f ( x ; θ ) ∣ θ ∈ R D } o r F = { P ∣ P ( Y ∣ X ; θ ) , θ ∈ R D } \mathcal H = \{ f(x;\theta) | \theta \in \mathbb{R}^D\} \\ or \quad \mathcal F = \{P|P(Y|X;\theta),\theta \in \mathbb{R}^D\} H = { f ( x ; θ ) ∣ θ ∈ R D } or F = { P ∣ P ( Y ∣ X ; θ ) , θ ∈ R D } f ( x ; θ ) f(x; \theta) f ( x ; θ ) θ \theta θ 决策函数 ),也称为模型(Model),参数向量θ \theta θ D D D R D \mathbb{R}^D R D D D D
模型的假设空间(hypothesis space)包含所有可能的条件概率分布或决策函数
特征空间(feature space) :
输入空间中的一个输入向量x = ( x 1 , x 2 ) x = (x_1,x_2) x = ( x 1 , x 2 ) x 1 2 , x 1 x 2 , x 2 2 , . . . x_1^2,x_1x_2,x_2^2,... x 1 2 , x 1 x 2 , x 2 2 , ...
统计学习的三要素 :
模型的假设空间(hypothesis space),简称:模型(model)。假设空间即我们对模型形式的先验假设,最终我们求得的模型必定符合我们对模型形式的先验假设。
模型选择的准则(evaluation criterion),简称:策略(strategy)或者学习准则。即我们用什么标准来评价一个模型的好坏。策略决定了我们从假设空间中选择模型的偏好。
模型学习的算法(algorithm),简称:算法(algorithm)。优化算法指的是通过什么样的方式调整我们的模型结构或模型超参数取值,使得模型的目标函数取值不断降低。优化算法决定了我们用什么样的步骤在假设空间中寻找合适的模型。
以线性回归(Linear Regression)为例:f ( x ; w , b ) = w T x + b f(x;w,b) = w^Tx +b f ( x ; w , b ) = w T x + b L ( y , y ^ ) = ( y − f ( x , θ ) ) 2 \mathcal L(y,\hat{y}) = (y-f(x,\theta))^2 L ( y , y ^ ) = ( y − f ( x , θ ) ) 2
机器学习的定义 :
graph LR;
F(["未知的目标函数(理想中完美的函数):𝑓: 𝒙⟶𝑦"])-->D["训练样本D:{(𝒙¹,𝑦¹),...,(𝒙ⁿ,𝑦ⁿ)}"];
D-->A{{"算法"}}
H{{"假设空间"}}-->A
A-->G["模型 g≈f"]
使用训练数据来计算接近目标 𝑓 的假设(hypothesis )g (来自:Machine Learning Foundations(机器学习基石)- the learning problem,25 页 )
监督学习 :学习输入到输出的映射的统计规律 。
输入变量与输出变量均为连续变量的预测问题称为回归问题 ;分类问题 ;标注问题 (分类问题的推广,如:隐马尔可夫模型 HMM,条件随机场 CRF)。
监督学习的模型可以是概率模型或非概率模型,由条件概率分布 P ( Y ∣ X ) P(Y|X) P ( Y ∣ X ) 决策函数(decision function) Y = f ( X ) Y=f(X) Y = f ( X ) P ( y ∣ x ) P(y|x) P ( y ∣ x ) Y = f ( x ) Y=f(x) Y = f ( x ) y = arg max y P ( y ∣ x ) y =\displaystyle\argmax_{y} P(y|x) y = y arg max P ( y ∣ x )
联合概率分布 :P ( X , Y ) P(X,Y) P ( X , Y ) P ( X , Y ) P(X,Y) P ( X , Y ) 训练数据与测试数据被看作是依联合概率分布P ( X , Y ) P(X,Y) P ( X , Y ) 。X X X Y Y Y
非监督学习 :学习数据中的统计规律或潜在结构 。
非监督学习的模型可以表示为函数z = g ( x ) z = g(x) z = g ( x ) P ( z ∣ x ) P(z|x) P ( z ∣ x ) z z z 聚类 或者降维 )z = arg max z P ( z ∣ x ) z =\displaystyle\argmax_{z} P(z|x) z = z arg max P ( z ∣ x ) P ( x ∣ z ) P(x|z) P ( x ∣ z ) 概率密度估计 ,比如 GMM 中P ( x ∣ z ) P(x|z) P ( x ∣ z ) z z z
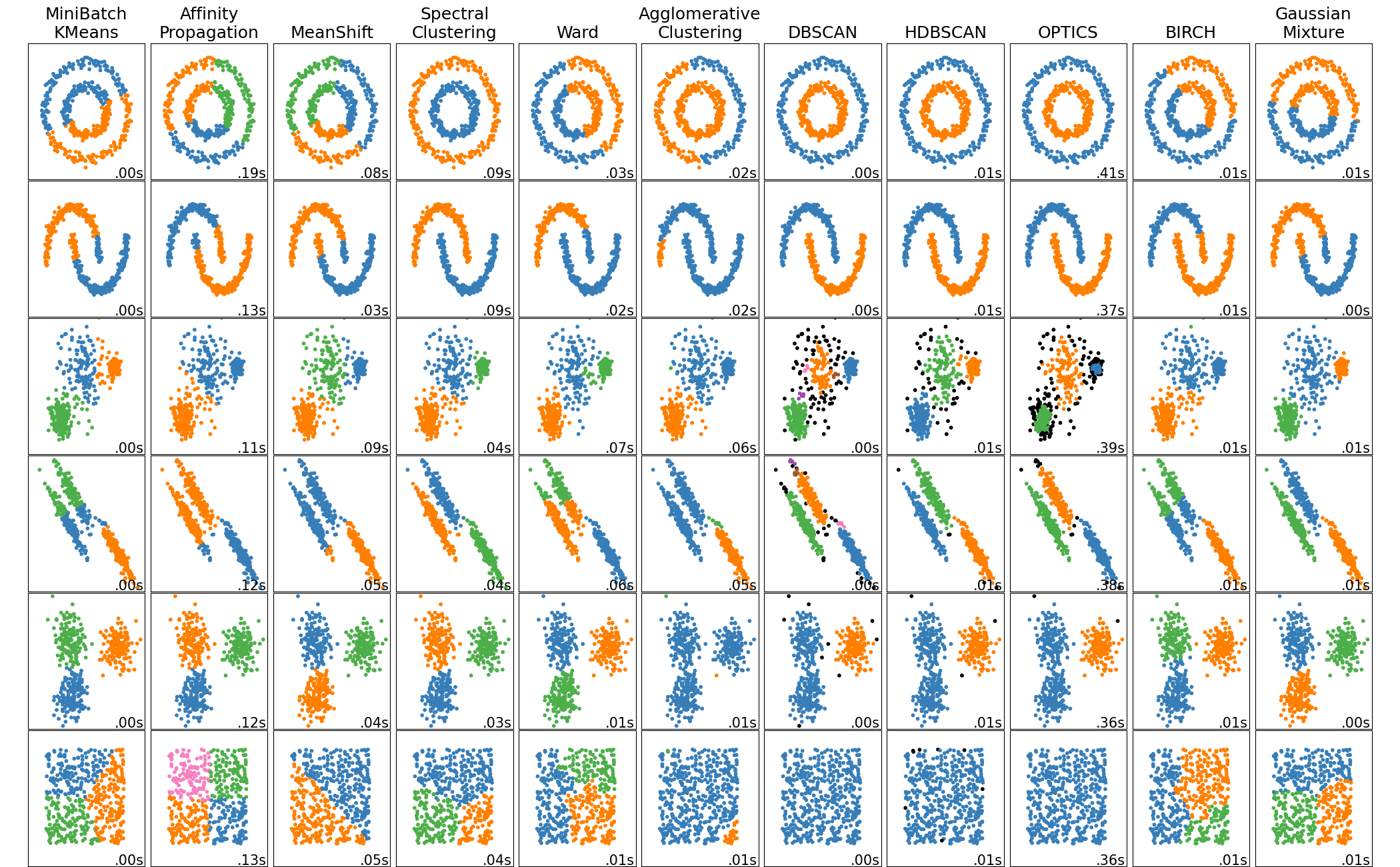
核密度估计 Kernel Density Estimation. - 应用密度估计检测离群值(outlier)的LocalOutlierFactor
概率模型(probabilistic model)与非概率模型(non-probabilistic model)或者确定性模型(deterministic model) :
概率模型(probabilistic model)- 条件概率分布 P(y|x)和 非概率模型(non-probabilistic model) - 函数 y=f(x)可以相互转化 ,条件概率分布最大化后得到函数,函数归一化后得到条件概率分布。所以概率模型与非概率模型的区别不在于输入输出之间的映射关系,而在于模型的内部结构:概率模型一定可以表示为联合概率分布的形式,而非概率模型则不一定存在这样的联合概率分布。
概率模型的代表是概率图模型(probabilistic graphical model) 参考文献 [ 1 − 3 ] ^{参考文献[1-3]} 参考文献 [ 1 − 3 ] P ( x ) = ∑ y P ( x , y ) P ( x , y ) = P ( x ) P ( y ∣ x ) P(x) = \sum_yP(x,y) \\ P(x,y) = P(x)P(y|x) P ( x ) = y ∑ P ( x , y ) P ( x , y ) = P ( x ) P ( y ∣ x )
参数化模型(parametric model)和非参数化模型(non-parametric model) :
参数化模型假设模型参数的维度固定,模型可以由有限维参数完全刻画,不随数据点的变化而变化。(如:感知机、GMM、logistic regression、朴素贝叶斯、k 均值聚类、潜在语义分析、概率潜在语义分析、潜在狄利克雷分配)
非参数化模型意味着决策树没有假设空间分布和分类器结构?
在线学习(online learning)和批量学习(batch learning) :
在线学习每次接受一个样本,预测后学习模型,并不断重复该操作。
在线学习比批量学习更难,因为每次模型更新中可利用的数据有限。
贝叶斯学习(Bayesian learning)/ 贝叶斯推理(Bayesian inference) :B a y e s R u l e : P ( X ∣ Y ) ⏟ p o s t e r i o r = P ( Y ∣ X ) ⏞ l i k e l i h o o d P ( X ) ⏞ p r i o r P ( Y ) ⏟ e v i d e n c e = P ( Y ∣ X ) ⏞ l i k e l i h o o d P ( X ) ⏞ p r i o r ∑ x P ( Y ∣ X ) P ( X ) ⏟ e v i d e n c e \mathrm{Bayes \; Rule:} \\ \underbrace{P(X|Y)}_{\mathrm{posterior}} = \frac{\overbrace{P(Y|X)}^{\mathrm{likelihood}}\overbrace{P(X)}^{\mathrm{prior}}}{\underbrace{P(Y)}_{\mathrm{evidence}}} = \frac{\overbrace{P(Y|X)}^{\mathrm{likelihood}}\overbrace{P(X)}^{\mathrm{prior}}}{\underbrace{\sum_{x}P(Y|X)P(X)}_{\mathrm{evidence}}} Bayes Rule : posterior P ( X ∣ Y ) = evidence P ( Y ) P ( Y ∣ X ) likelihood P ( X ) prior = evidence x ∑ P ( Y ∣ X ) P ( X ) P ( Y ∣ X ) likelihood P ( X ) prior
核技巧(kernel trick)/ 核方法(kernel method) :
核方法 是一类把低维空间的非线性可分问题,转化为高维空间的线性可分问题的方法。核技巧 是一种利用核函数直接计算 ⟨ ϕ ( x ) , ϕ ( z ) ⟩ \lang \phi(x),\phi(z) \rang ⟨ ϕ ( x ) , ϕ ( z )⟩ ϕ ( x ) \phi(x) ϕ ( x ) ϕ ( z ) \phi(z) ϕ ( z )
核函数 :Kernel function X \mathcal X X x i ∈ X x_i \in \mathcal X x i ∈ X X \mathcal X X R n \mathbb R^n R n H \mathcal H H 附加知识 : 各种空间介绍 ^{附加知识:各种空间介绍} 附加知识 : 各种空间介绍 X \mathcal X X H \mathcal H H
ϕ ( x ) : X → H \phi(x) : \mathcal X \to \mathcal H ϕ ( x ) : X → H
使得对所有 x , z ∈ X x,z \in \mathcal X x , z ∈ X K ( x , z ) K(x,z) K ( x , z )
K ( x , z ) = ϕ ( x ) . ϕ ( z ) = ⟨ ϕ ( x ) , ϕ ( z ) ⟩ K(x,z) = \phi(x).\phi(z) = \lang \phi(x),\phi(z) \rang K ( x , z ) = ϕ ( x ) . ϕ ( z ) = ⟨ ϕ ( x ) , ϕ ( z )⟩
则称 K ( x , z ) K(x,z) K ( x , z ) ϕ ( x ) \phi(x) ϕ ( x ) ⟨ ϕ ( x ) , ϕ ( z ) ⟩ \lang \phi(x),\phi(z) \rang ⟨ ϕ ( x ) , ϕ ( z )⟩
核技巧 的想法是,在学习和预测中只定义核函数 K ( x , z ) K(x,z) K ( x , z ) ϕ \phi ϕ K ( x , z ) K(x,z) K ( x , z ) ϕ ( x ) \phi(x) ϕ ( x ) ϕ ( z ) \phi(z) ϕ ( z ) K ( x , z ) K(x,z) K ( x , z )
注意:ϕ \phi ϕ R n \mathbb{R}^n R n H \mathcal H H H \mathcal H H ϕ \phi ϕ 维度灾难 又称维度诅咒(Curse of Dimensionality) 附加知识 : 维度诅咒 ^{附加知识:维度诅咒} 附加知识 : 维度诅咒
正则化符合奥卡姆剃刀(Occam's razor)原理。
参考:L1L2 正则化和凸优化
参考:模型选择
参考:生成模型和判别模型
线性空间 就是定义了加法和数乘 的空间(空间里的一个元素就可以由其他元素线性表示)。
度量空间 就是定义了距离 的空间(曼哈顿距离,欧氏距离,闵可夫斯基距离,马氏距离,切比雪夫距离)。
非负性、同一性:d i s t ( x i , x j ) ≥ 0 dist(x_i,x_j) \geq 0 d i s t ( x i , x j ) ≥ 0 d i s t ( x i , x j ) = 0 dist(x_i,x_j) = 0 d i s t ( x i , x j ) = 0 x i = x j x_i=x_j x i = x j
对称性:d i s t ( x i , x j ) = d i s t ( x j , x i ) dist(x_i,x_j) = dist(x_j,x_i) d i s t ( x i , x j ) = d i s t ( x j , x i )
三角不等式(也叫直递性):d i s t ( x i , x j ) ≤ d i s t ( x i , x k ) + d i s t ( x k , x j ) dist(x_i,x_j) \leq dist(x_i,x_k) + dist(x_k,x_j) d i s t ( x i , x j ) ≤ d i s t ( x i , x k ) + d i s t ( x k , x j )
文字解释:【两点之间距离不为负;两个点只有在 空间 上重合才可能距离为零;a 到 b 的距离等于 b 到 a 的距离;a 到 c 的距离加上 c 到 b 的距离大于等于 a 直接到 b 的距离;】
赋范空间 就是定义了范数 的空间。长度 。那么这里的长度和上一节中说的距离到底有什么区别呢。距离的概念是针对两个元素来说的 ,例如 d(x,y)指的是 x 与 y 两个元素之间的距离,而范数是针对一个元素来说的 ,每一个元素都对应一个范数,可以将范数理解为一个元素到零点的距离(这只是一种理解,并不是定义),也就是它自己的长度。∣ ∣ . ∣ ∣ : R n → R ||.|| : \mathbb{R}^n \to \mathbb{R} ∣∣.∣∣ : R n → R R n \mathbb{R}^n R n
非负性: ∀ x ∈ R n , ∣ ∣ x ∣ ∣ ≥ 0 \forall x \in \mathbb{R}^n ,||x|| \geq 0 ∀ x ∈ R n , ∣∣ x ∣∣ ≥ 0 ∣ ∣ x ∣ ∣ = 0 ||x|| = 0 ∣∣ x ∣∣ = 0 x = 0 x=0 x = 0
数乘:∀ x ∈ R n , a ∈ R n , ∣ ∣ a x ∣ ∣ = ∣ a ∣ . ∣ ∣ x ∣ ∣ \forall x \in \mathbb{R}^n ,a \in \mathbb{R}^n, ||ax|| = |a|.||x|| ∀ x ∈ R n , a ∈ R n , ∣∣ a x ∣∣ = ∣ a ∣.∣∣ x ∣∣
三角不等式: ∀ x , y ∈ R n , ∣ ∣ x + y ∣ ∣ ≤ ∣ ∣ x ∣ ∣ + ∣ ∣ y ∣ ∣ \forall x,y \in \mathbb{R}^n ,||x+y|| \leq ||x|| + ||y|| ∀ x , y ∈ R n , ∣∣ x + y ∣∣ ≤ ∣∣ x ∣∣ + ∣∣ y ∣∣
如果我们定义了范数,可以在这基础上定义距离:dist(x,y)=||x-y||。根据范数的三条性质,我们可以证明我们这样定义的距离也满足距离的定义,聪明的你可以自己证明一下(对称性的证明,提一个-1 出来,一加绝对值就是 1 了)。
也就是说范数其实是一个更加具体的概念,有了范数一定能利用范数定义距离,但是有距离不能定义范数 。
也许你会问,你不是说理解范数就是一个元素到零点的距离吗,那定义范数为||x||=dist(x,0) 不就行了吗。这样的话,对于范数的第二条性质就不一定会满足,||ax||=dist(ax,0),而 dist(ax,0)不一定等于|a|dist(x,0),具体等不等于还要看你的距离是怎么定义的。
例如:Lp 范数p 范数:当 p>=1 时,向量的 Lp 范数是凸的。(这也是为什么一般不用 L0 范数的原因之一)
线性赋范空间 就是定义了加法、数乘和范数的空间。
巴拿赫空间 就是完备的赋范线性空间 。(Banach space)完备的空间 的定义:如果一个空间是完备的,那么该空间中的任何一个柯西序列都收敛在该空间之内。
首先来说一下柯西序列是什么,柯西序列就是随着序数增加,值之间的距离越来越小的序列。换一种说法是,柯西序列可以在去掉有限个值之后,使任意两个值之间的距离 ‾ \underline{\mathrm{距离}} 距离
那么任意一个柯西序列都收敛在该空间内是什么意思呢,举个例子你就明白了。
设定义在有理数空间 Q 上的序列:x n = [ 2 n ] n x_n = \frac{[\sqrt{2}n]}{n} x n = n [ 2 n ] x n x_n x n 2 \sqrt{2} 2
所以完备的意义我们可以这样理解,那就是在一个空间上我们定义了极限,但是不论你怎么取极限,它的极限的值都不会跑出这个空间,那么这个空间就是完备空间 。
另外,不知道你有没有发现,上面在解释什么是柯西序列的时候,有一个词我加了下划线,那就是距离,也就说说在定义完备空间之前,要先有距离的概念。所以完备空间,其实也是完备度量空间 。
所以,巴拿赫空间满足几条特性呢:距离、范数、完备。
内积空间 就是定义了内积的空间。Inner product space
定义映射⟨ . , . ⟩ : V × V → F \lang .,. \rang : V \times V \to \mathbb{F} ⟨ . , . ⟩ : V × V → F V V V F \mathbb{F} F x , y , z ∈ V , s ∈ F x,y,z \in V ,s \in \mathbb{F} x , y , z ∈ V , s ∈ F
第一个参数中的线性:⟨ s x , y ⟩ = s ⟨ x , y ⟩ ⟨ x + y , z ⟩ = ⟨ x , z ⟩ + ⟨ y , z ⟩ ⟨ 0 , x ⟩ = 0 \lang sx,y \rang = s\lang x,y \rang \\ \lang x+y,z \rang = \lang x,z \rang + \lang y,z \rang \\ \lang 0,x \rang = 0 ⟨ s x , y ⟩ = s ⟨ x , y ⟩ ⟨ x + y , z ⟩ = ⟨ x , z ⟩ + ⟨ y , z ⟩ ⟨ 0 , x ⟩ = 0
共轭对称:⟨ x , y ⟩ = ⟨ y , x ⟩ ‾ \lang x,y \rang = \overline{\lang y,x \rang } ⟨ x , y ⟩ = ⟨ y , x ⟩
正定性:⟨ x , x ⟩ > 0 i f x ≠ 0 \lang x,x \rang > 0 \quad\mathrm{if}\; x \neq 0 ⟨ x , x ⟩ > 0 if x = 0
正半定性或非负定性:∀ x , ⟨ x , x ⟩ ≥ 0 \forall{x}, \lang x,x \rang \geq 0 ∀ x , ⟨ x , x ⟩ ≥ 0
确定性:⟨ x , x ⟩ = 0 必然有 x = 0 \lang x,x \rang = 0 必然有 x=0 ⟨ x , x ⟩ = 0 必然有 x = 0
3,4,5 可以跟上面定义范数和距离一样写成一个
例子-欧几里得向量空间:x , y ∈ R n , ⟨ x , y ⟩ = x T y = ∑ _ i = 1 n x i y i x,y \in \mathbb{R}^n , \lang x,y \rang = x^Ty=\sum\_{i=1}^n{x_iy_i} x , y ∈ R n , ⟨ x , y ⟩ = x T y = ∑ _ i = 1 n x i y i
只有定义了内积,才会有夹角的概念,才会有正交的概念,另外内积也可以定义范数,也就是说内积是比范数更具体的一个概念。
欧式空间 就是定义了内积的有限维实线性空间。
希尔伯特空间 就是完备的内积空间。(Hilbert space)
graph LR;
LS(("Linear Space"))-->NLS(("Normed Linear Space"));
NLS-->BS(("Banach Space"))
NLS-->IPS(("Inner Product Space"))
IPS-->HS(("Hilbert Space"))
IPS-->ES(("Euclid Space"))
参考:一片文章带你理解再生核希尔伯特空间(RKHS)以及各种空间
维度诅咒通常是指在涉及到向量的计算的问题中,随着维数的增加,计算量呈指数倍增长的一种现象。高维度有更大的特征空间,需要更多的数据才可以进行较准确的估计。
若特征是二值的,则每增加一个特征,所需数据量都在以 2 的指数级进行增长,更何况很多特征不只是二值的。
几何角度 1:
background
Layer 1
0.5
上图表示一个多维空间(以二维为例),设正方形边长为 1,则其内切圆半径为r = 0.5 r=0.5 r = 0.5 π ( 0.5 ) 2 \pi(0.5)^2 π ( 0.5 ) 2 4 3 π ( 0.5 ) 3 \frac{4}{3}\pi(0.5)^3 3 4 π ( 0.5 ) 3
因此球体的体积可以表示为V ( d ) = π d / 2 Γ ( d 2 + 1 ) 0. 5 d = k ( 0.5 ) d V(d) = \frac{\pi^{d/2}}{\varGamma(\frac{d}{2}+1)}0.5^d = k(0.5)^d V ( d ) = Γ ( 2 d + 1 ) π d /2 0. 5 d = k ( 0.5 ) d lim d → ∞ k ( 0.5 ) d = 0 \lim_{d \to \infty}k(0.5)^d = 0 lim d → ∞ k ( 0.5 ) d = 0 高维情况下,数据大都分布在四角(正方形内,内切圆外) ,稀疏性太大,不好分类。
维度越大,超球体体积越小。说明落在超球体内的样本越少,因为超球体是超立方体的内切球。不在球内,那只能在角落!
几何角度 2:
background
Layer 1
上图也表示一个多维空间(以二维为例),则其中图形的体积有如下关系:外圆半径r = 1 r=1 r = 1 r − ε r−\varepsilon r − ε V 外圆 = k . 1 d = k V_{外圆} = k.1^d = k V 外圆 = k . 1 d = k V 圆环 = k − k ( 1 − ε ) d V_{圆环} = k - k(1-\varepsilon)^d V 圆环 = k − k ( 1 − ε ) d lim d → ∞ V 圆环 V 外圆 = lim d → ∞ k − k ( 1 − ε ) d k = lim d → ∞ ( 1 − ( 1 − ε ) d ) = 1 \lim_{d \to \infty}\frac{V_{圆环}}{V_{外圆}} = \lim_{d \to \infty}\frac{ k - k(1-\varepsilon)^d}{k} = \lim_{d \to \infty}(1-(1-\varepsilon)^d) = 1 d → ∞ lim V 外圆 V 圆环 = d → ∞ lim k k − k ( 1 − ε ) d = d → ∞ lim ( 1 − ( 1 − ε ) d ) = 1
高维情况下,无论ε \varepsilon ε 稀疏 。
参考:The Curse of Dimensionality in classification 机器学习-白板推导系列(五)-降维(Dimensionality Reduction)
所有不等式 以及所有概率(Probabilistic)不等式
由 KL divergence 就能证明D K L ( P ∥ Q ) ≡ ∑ i = 1 n p i log p i q i ≥ 0. {\displaystyle D_{\mathrm {KL} }(P\|Q)\equiv \sum _{i=1}^{n}p_{i}\log {\frac {p_{i}}{q_{i}}}\geq 0.} D KL ( P ∥ Q ) ≡ i = 1 ∑ n p i log q i p i ≥ 0.
柯西-施瓦茨 (Cauchy–Schwarz) 不等式 - Cauchy–Schwarz inequality [ ∑ i = 1 n a i b i ] 2 ≤ [ ∑ i = 1 n a i 2 ] . [ ∑ i = 1 n b i 2 ] 等式成立: b i = k a i 向量形式: ∣ ⟨ u , v ⟩ ∣ ≤ ∣ ∣ u ∣ ∣ . ∣ ∣ v ∣ ∣ 概率中: ∣ E ( X Y ) ∣ 2 ≤ E ( X 2 ) E ( Y 2 ) [\sum_{i=1}^{n}{a_ib_i}]^2 \leq [\sum_{i=1}^{n}a_i^2].[\sum_{i=1}^{n}b_i^2] 等式成立:b_i=ka_i \\ 向量形式:|\braket{u,v}| \leq ||u||.||v|| \\ 概率中:|E(XY)|^2 \leq E(X^2)E(Y^2) [ i = 1 ∑ n a i b i ] 2 ≤ [ i = 1 ∑ n a i 2 ] . [ i = 1 ∑ n b i 2 ] 等式成立: b i = k a i 向量形式: ∣ ⟨ u , v ⟩ ∣ ≤ ∣∣ u ∣∣.∣∣ v ∣∣ 概率中: ∣ E ( X Y ) ∣ 2 ≤ E ( X 2 ) E ( Y 2 ) A ⃗ = ( a 1 , . . . , a n ) , B ⃗ = ( b 1 , . . . , b n ) A ⃗ . B ⃗ = ( a 1 b 1 , . . . , a n b n ) = ∣ ∣ A ⃗ ∣ ∣ . ∣ ∣ B ⃗ ∣ ∣ cos θ ≤ ∣ ∣ A ⃗ ∣ ∣ . ∣ ∣ B ⃗ ∣ ∣ = a 1 2 + . . . + a n 2 . b 1 2 + . . . + b n 2 \vec{A} = (a_1,...,a_n), \vec{B} = (b_1,...,b_n) \\ \vec{A}.\vec{B} = (a_1b_1,...,a_nb_n) = ||\vec{A}||.||\vec{B}||\cos\theta \leq ||\vec{A}||.||\vec{B}|| = \sqrt{a_1^2+...+a_n^2}.\sqrt{b_1^2+...+b_n^2} A = ( a 1 , ... , a n ) , B = ( b 1 , ... , b n ) A . B = ( a 1 b 1 , ... , a n b n ) = ∣∣ A ∣∣.∣∣ B ∣∣ cos θ ≤ ∣∣ A ∣∣.∣∣ B ∣∣ = a 1 2 + ... + a n 2 . b 1 2 + ... + b n 2
证明 covariance inequality:V a r ( Y ) ≥ C o v ( Y , X ) 2 V a r ( X ) Var(Y) \geq \frac{Cov(Y,X)^2}{Var(X)} Va r ( Y ) ≥ Va r ( X ) C o v ( Y , X ) 2 ⟨ X , Y ⟩ : = E ( X Y ) \braket{X,Y} := E(XY) ⟨ X , Y ⟩ := E ( X Y ) ∣ C o v ( Y , X ) ∣ 2 = ∣ E ( ( X − μ ) ( Y − v ) ) ∣ 2 = ∣ ⟨ X − μ , Y − v ⟩ ∣ 2 ≤ ⟨ X − μ , X − μ ⟩ ⟨ Y − v , Y − v ⟩ = E ( ( X − μ ) 2 ) E ( ( Y − v ) 2 ) = V a r ( X ) V a r ( Y ) |Cov(Y,X)|^2 = |E((X-\mu)(Y-v))|^2 = |\braket{X-\mu,Y-v}|^2 \\ \leq \braket{X-\mu,X-\mu}\braket{Y-v,Y-v} = E((X-\mu)^2)E((Y-v)^2) = Var(X)Var(Y) ∣ C o v ( Y , X ) ∣ 2 = ∣ E (( X − μ ) ( Y − v )) ∣ 2 = ∣ ⟨ X − μ , Y − v ⟩ ∣ 2 ≤ ⟨ X − μ , X − μ ⟩ ⟨ Y − v , Y − v ⟩ = E (( X − μ ) 2 ) E (( Y − v ) 2 ) = Va r ( X ) Va r ( Y )
赫尔德 (Holder) 不等式 - Hölder's inequality
琴生 (Jensen) 不等式 - Jensen's inequality f ( t x 1 + ( 1 − t ) x 2 ) ≤ t f ( x 1 ) + ( 1 − t ) f ( x 2 ) , f is convex function 推广: f ( a 1 x 1 + . . . + a n x n ) ≤ a 1 f ( x 1 ) + . . . + a n f ( x n ) , a 1 + . . . + a n = 1 , a i ≥ 0 o r : f ( ∑ i = 1 n a i x i ) ≤ ∑ i = 1 n a i f ( x i ) , ∑ i = 1 n a i = 1 , a i ≥ 0 f(tx_1 +(1-t)x_2) \leq tf(x_1) + (1-t)f(x_2), \text{f is convex function} \\ 推广:f(a_1x_1 +...+ a_nx_n) \leq a_1f(x_1) +...+ a_nf(x_n), a_1+...+a_n = 1 , a_i \geq 0 \\ or: f(\sum_{i=1}^n{a_ix_i}) \leq \sum_{i=1}^n{a_if(x_i)} , \sum_{i=1}^n{a_i} = 1, a_i \geq 0 f ( t x 1 + ( 1 − t ) x 2 ) ≤ t f ( x 1 ) + ( 1 − t ) f ( x 2 ) , f is convex function 推广: f ( a 1 x 1 + ... + a n x n ) ≤ a 1 f ( x 1 ) + ... + a n f ( x n ) , a 1 + ... + a n = 1 , a i ≥ 0 or : f ( i = 1 ∑ n a i x i ) ≤ i = 1 ∑ n a i f ( x i ) , i = 1 ∑ n a i = 1 , a i ≥ 0
概率中:如果X X X φ \varphi φ φ ( E [ X ] ) ≤ E [ φ ( X ) ] \varphi(E[X]) \leq E[\varphi(X)] φ ( E [ X ]) ≤ E [ φ ( X )] E [ φ ( X ) ] − φ ( E [ X ] ) E[\varphi(X)] - \varphi(E[X]) E [ φ ( X )] − φ ( E [ X ])
EM 算法中有用到(log 函数是凹函数正好与凸函数相反);
证明 KL 散度>=0;
马尔可夫不等式 - Markov's inequality P ( X ≥ a ) ≤ E ( X ) a P(X \geq a) \leq \frac{E(X)}{a} P ( X ≥ a ) ≤ a E ( X ) X X X ∀ a > 0 \forall a>0 ∀ a > 0
用于估计一个概率的上界,比如假设你所在公司的人均工资是 1 万,那么随机选一个你司员工,其工资超过 10 万的概率,不会超过 1/10;
用于其他概率不等式的证明,比如霍夫丁不等式;
切比雪夫 (Chebyshev) 不等式 - Chebyshev's inequality P { ∣ X − μ ∣ ≥ k } ≤ σ 2 k 2 P\{|X-\mu| \geq k\} \leq \frac{\sigma^2}{k^2} P { ∣ X − μ ∣ ≥ k } ≤ k 2 σ 2 X X X ∀ k > 0 \forall k>0 ∀ k > 0 μ \mu μ σ 2 \sigma^2 σ 2
霍夫丁不等式 - Hoeffding's inequality
Machine Learning Foundations(机器学习基石)- feasibility of learning,12,13,18 页 统计学习方法,26 页,证明泛化误差上界(在机器学习中常用的几个概率不等式及证明 中也有提到)
参考:初等数学学习笔记
[1-1] Hastie T,Tibshirani R,Friedman J. The Elements of Statistical Learning: DataMining,Inference,and Prediction . Springer. 2001(中译本:统计学习基础——数据挖掘、推理与预测。范明,柴玉梅,昝红英等译。北京:电子工业出版社,2004)
[1-2] Bishop M. Pattern Recognition and Machine Learning . Springer,2006
[1-3] Probabilistic Graphical Models: Principles and Techniques by Daphne Koller, Nir Friedman from The MIT Press
[1-4] Deep Learning (Ian Goodfellow, Yoshua Bengio, Aaron Courville)
[1-5] Tom M Michelle. Machine Learning . McGraw-Hill Companies,Inc. 1997(中译本:机器学习。北京:机械工业出版社,2003)
[1-6] Bayesian Reasoning and Machine Learning by David Barber 2007–2020 ,other version
[1-7] Reinforcement Learning:An Introduction (second edition 2020) by Richard S. Sutton and Andrew G. Barto ,other version
[1-8] 周志华,机器学习 ,清华大学出版社 (手推笔记 以及 公式推导解析 )
[1-9] Lecture Notes in MACHINE LEARNING Dr V N Krishnachandran
判别模型
感知机Perceptron 是神经网络 和支持向量机 的基础。最早在 1957 年由 Rosenblatt 提出参考文献 [ 2 − 1 ] ^{参考文献[2-1]} 参考文献 [ 2 − 1 ] 参考文献 [ 2 − 2 ] ^{参考文献[2-2]} 参考文献 [ 2 − 2 ] 参考文献 [ 2 − 3 ] ^{参考文献[2-3]} 参考文献 [ 2 − 3 ] 参考文献 [ 2 − 4 ] ^{参考文献[2-4]} 参考文献 [ 2 − 4 ] 参考文献 [ 2 − 5 ] ^{参考文献[2-5]} 参考文献 [ 2 − 5 ] 参考文献 [ 2 − 6 ] ^{参考文献[2-6]} 参考文献 [ 2 − 6 ] Brief History of Machine Learning
要求:数据集线性可分(linearly separable data set)
模型 :f ( x ) = s i g n ( w . x + b ) f(x) = sign(w.x + b) f ( x ) = s i g n ( w . x + b ) x , w ∈ R n , b ∈ R x,w \in \mathbb{R}^n ,b \in \mathbb{R} x , w ∈ R n , b ∈ R w w w b b b s i g n ( x ) = { + 1 x ≥ 0 − 1 x < 0 sign(x) = \begin{cases}
+1 & x \geq 0 \\
-1 & x<0
\end{cases} s i g n ( x ) = { + 1 − 1 x ≥ 0 x < 0
感知机是一种线性分类模型,属于判别模型。感知机模型的假设空间是定义在特征空 间中的所有线性分类模型(linear classification model)或线性分类器(linear classifier),即 函数集合{ f ∣ f ( x ) = w ⋅ x + b } \{f|f(x)=w·x+b\} { f ∣ f ( x ) = w ⋅ x + b }
超平面 S:w . x + b = 0 w.x+b = 0 w . x + b = 0 w w w b b b
策略 :L ( w , b ) = − ∑ x i ∈ M y i ( w . x i + b ) L(w,b) = -\sum_{x_i \in M}{y_i(w.x_i + b)} L ( w , b ) = − x i ∈ M ∑ y i ( w . x i + b ) M M M M = { ( x i , y i ) ∣ − y i ( w . x i + b ) > 0 } M = \{ (x_i,y_i)|-y_i(w.x_i +b) > 0\} M = {( x i , y i ) ∣ − y i ( w . x i + b ) > 0 }
函数间隔:y ( w . x + b ) y(w.x + b) y ( w . x + b ) 1 ∣ ∣ w ∣ ∣ ∣ w . x + b ∣ \frac{1}{||w||}|w.x + b| ∣∣ w ∣∣ 1 ∣ w . x + b ∣ 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣ w ∣∣ 1
算法 :min w , b L ( w , b ) = − ∑ x i ∈ M y i ( w . x i + b ) \min_{w,b} L(w,b) = -\sum_{x_i \in M}{y_i(w.x_i + b)} w , b min L ( w , b ) = − x i ∈ M ∑ y i ( w . x i + b ) 随机梯度下降法(stochastic gradient) :
初始化参数(随机法):w 0 , b 0 w_0,b_0 w 0 , b 0
选取数据( x i , y i ) (x_i,y_i) ( x i , y i )
如果( x i , y i ) (x_i,y_i) ( x i , y i ) y i ( w . x i + b ) ≤ 0 y_i(w.x_i + b) \leq 0 y i ( w . x i + b ) ≤ 0 w , b w,b w , b 在 ( x i , y i ) 点处梯度为: ∇ w L ( w , b ) = − y i x i ∇ b L ( w , b ) = − y i 更新 w : w k + 1 ← w k + η y i x i 更新 b : b k + 1 ← b k + η y i 其中学习率 η ∈ ( 0 , 1 ] 在(x_i,y_i)点处梯度为:\\ \nabla_wL(w,b) = -y_ix_i \\ \nabla_bL(w,b) = -y_i\\ 更新w:w_{k+1} \gets w_{k}+\eta y_ix_i \\ 更新b:b_{k+1} \gets b_{k}+\eta y_i \\其中学习率\eta \in (0,1] 在 ( x i , y i ) 点处梯度为: ∇ w L ( w , b ) = − y i x i ∇ b L ( w , b ) = − y i 更新 w : w k + 1 ← w k + η y i x i 更新 b : b k + 1 ← b k + η y i 其中学习率 η ∈ ( 0 , 1 ]
循环 2-3,直到训练集中没有误分类点。
Novikoff 定理:T = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } T = \{(x_1,y_1),...,(x_N,y_N)\} T = {( x 1 , y 1 ) , ... , ( x N , y N )}
设完美超平面w ^ o p t . x ^ = 0 , ∣ ∣ w ^ o p t ∣ ∣ = 1 \hat{w}_{opt}.\hat{x} = 0 , ||\hat{w}_{opt}||=1 w ^ o pt . x ^ = 0 , ∣∣ w ^ o pt ∣∣ = 1 w ^ o p t . x ^ = w o p t . x + b \hat{w}_{opt}.\hat{x} = w_{opt}.x +b w ^ o pt . x ^ = w o pt . x + b γ > 0 \gamma >0 γ > 0 y i ( w ^ o p t . x i ^ ) ≥ γ y_i(\hat{w}_{opt}.\hat{x_i}) \geq \gamma y i ( w ^ o pt . x i ^ ) ≥ γ
令R = max 1 ≤ i ≤ N ∣ ∣ x i ^ ∣ ∣ R = \max_{1\leq i\leq N}||\hat{x_i}|| R = max 1 ≤ i ≤ N ∣∣ x i ^ ∣∣ k ≤ ( R γ ) 2 k \leq (\frac{R}{\gamma})^2 k ≤ ( γ R ) 2
证明(注意:带 hat 的表示扩充向量):
因为数据线性可分,对于所有点y i ( w ^ o p t . x i ^ ) > 0 y_i(\hat{w}_{opt}.\hat{x_i}) > 0 y i ( w ^ o pt . x i ^ ) > 0 γ = min i y i ( w ^ o p t . x i ^ ) ≤ y i ( w ^ o p t . x i ^ ) (2-1) \gamma = \min_i{y_i(\hat{w}_{opt}.\hat{x_i})} \leq {y_i(\hat{w}_{opt}.\hat{x_i})} \label{2-1}\tag{2-1} γ = i min y i ( w ^ o pt . x i ^ ) ≤ y i ( w ^ o pt . x i ^ ) ( 2-1 ) γ \gamma γ
为了方便计算 设 扩充向量w ^ = ( w T , b ) T \hat{w} = (w^T,b)^T w ^ = ( w T , b ) T w ^ k = w ^ k − 1 + η y i x i ^ (2-2) \hat{w}_{k} = \hat{w}_{k-1}+\eta y_i\hat{x_i} \label{2-2}\tag{2-2} w ^ k = w ^ k − 1 + η y i x i ^ ( 2-2 )
推导不等式w ^ k . w ^ o p t ≥ k η γ (2-3) \hat{w}_{k}.\hat{w}_{opt} \geq k\eta\gamma \label{2-3}\tag{2-3} w ^ k . w ^ o pt ≥ k η γ ( 2-3 )
由( 2-1 ) \eqref{2-1} ( 2-1 ) ( 2-2 ) \eqref{2-2} ( 2-2 ) w ^ k . w ^ o p t = w ^ k − 1 . w ^ o p t + η y i w ^ o p t . x i ^ ≥ w ^ k − 1 . w ^ o p t + η γ ≥ w ^ k − 2 . w ^ o p t + 2 η γ ≥ k η γ \hat{w}_{k}.\hat{w}_{opt} = \hat{w}_{k-1}.\hat{w}_{opt} + \eta{y_i}\hat{w}_{opt}.\hat{x_i} \\ \geq \hat{w}_{k-1}.\hat{w}_{opt} + \eta\gamma \\ \geq \hat{w}_{k-2}.\hat{w}_{opt} + 2\eta\gamma \\ \geq k\eta\gamma w ^ k . w ^ o pt = w ^ k − 1 . w ^ o pt + η y i w ^ o pt . x i ^ ≥ w ^ k − 1 . w ^ o pt + η γ ≥ w ^ k − 2 . w ^ o pt + 2 η γ ≥ k η γ
推导不等式∣ ∣ w ^ k ∣ ∣ 2 ≤ k η 2 R 2 (2-4) ||\hat{w}_{k}||^2 \leq k\eta^2R^2 \label{2-4}\tag{2-4} ∣∣ w ^ k ∣ ∣ 2 ≤ k η 2 R 2 ( 2-4 ) ( 2-2 ) \eqref{2-2} ( 2-2 ) ∣ ∣ w ^ k ∣ ∣ 2 = ∣ ∣ w ^ k − 1 + η y i x i ^ ∣ ∣ 2 = ∣ ∣ w ^ k − 1 ∣ ∣ 2 + 2 η y i w ^ k − 1 . x ^ i + η 2 ∣ ∣ x ^ i ∣ ∣ 2 ||\hat{w}_{k}||^2=||\hat{w}_{k-1}+\eta y_i\hat{x_i}||^2 = ||\hat{w}_{k-1}||^2 + 2\eta{y_i}\hat{w}_{k-1}.\hat{x}_{i} + \eta^2||\hat{x}_{i}||^2 ∣∣ w ^ k ∣ ∣ 2 = ∣∣ w ^ k − 1 + η y i x i ^ ∣ ∣ 2 = ∣∣ w ^ k − 1 ∣ ∣ 2 + 2 η y i w ^ k − 1 . x ^ i + η 2 ∣∣ x ^ i ∣ ∣ 2 y i w ^ k − 1 . x ^ i ≤ 0 {y_i}\hat{w}_{k-1}.\hat{x}_{i} \leq 0 y i w ^ k − 1 . x ^ i ≤ 0 ∣ ∣ w ^ k ∣ ∣ 2 = ∣ ∣ w ^ k − 1 ∣ ∣ 2 + 2 η y i w ^ k − 1 . x ^ i + η 2 ∣ ∣ x ^ i ∣ ∣ 2 ≤ ∣ ∣ w ^ k − 1 ∣ ∣ 2 + η 2 ∣ ∣ x ^ i ∣ ∣ 2 ≤ ∣ ∣ w ^ k − 1 ∣ ∣ 2 + η 2 R 2 ≤ ∣ ∣ w ^ k − 2 ∣ ∣ 2 + 2 η 2 R 2 ≤ . . . ≤ k η 2 R 2 ||\hat{w}_{k}||^2 =||\hat{w}_{k-1}||^2 + 2\eta{y_i}\hat{w}_{k-1}.\hat{x}_{i} + \eta^2||\hat{x}_{i}||^2 \\ \leq ||\hat{w}_{k-1}||^2 + \eta^2||\hat{x}_{i}||^2 \\ \leq ||\hat{w}_{k-1}||^2 + \eta^2R^2 \\ \leq ||\hat{w}_{k-2}||^2 + 2\eta^2R^2 \leq ... \\ \leq k\eta^2R^2 ∣∣ w ^ k ∣ ∣ 2 = ∣∣ w ^ k − 1 ∣ ∣ 2 + 2 η y i w ^ k − 1 . x ^ i + η 2 ∣∣ x ^ i ∣ ∣ 2 ≤ ∣∣ w ^ k − 1 ∣ ∣ 2 + η 2 ∣∣ x ^ i ∣ ∣ 2 ≤ ∣∣ w ^ k − 1 ∣ ∣ 2 + η 2 R 2 ≤ ∣∣ w ^ k − 2 ∣ ∣ 2 + 2 η 2 R 2 ≤ ... ≤ k η 2 R 2
由( 2-3 ) \eqref{2-3} ( 2-3 ) ( 2-4 ) \eqref{2-4} ( 2-4 )
k η γ ≤ w ^ k . w ^ o p t ≤ ∣ ∣ w ^ k ∣ ∣ . ∣ ∣ w ^ o p t ∣ ∣ ⏟ = 1 ⏟ 柯西-施瓦茨 (Cauchy–Schwarz) 不等式 ≤ k η R ⇒ k 2 γ 2 ≤ k R 2 ⇒ k ≤ ( R γ ) 2 k\eta\gamma \leq \underbrace{\hat{w}_{k}.\hat{w}_{opt} \leq ||\hat{w}_{k}||.\underbrace{||\hat{w}_{opt}||}_{=1} }_{\text{柯西-施瓦茨 (Cauchy–Schwarz) 不等式}} \leq \sqrt{k} \eta R \\ \; \\ \Rightarrow k^2\gamma^2 \leq kR^2 \\ \Rightarrow k \leq (\frac{R}{\gamma})^2 k η γ ≤ 柯西 - 施瓦茨 (Cauchy–Schwarz) 不等式 w ^ k . w ^ o pt ≤ ∣∣ w ^ k ∣∣. = 1 ∣∣ w ^ o pt ∣∣ ≤ k η R ⇒ k 2 γ 2 ≤ k R 2 ⇒ k ≤ ( γ R ) 2
也就是说 k 是有上界的。
书中还介绍了原形式的对偶形式 ,也就是等价形式(SVM 中 7.2.2 节 127 页也是等价的意思,区别于拉格朗日对偶),这两个地方的等价都是经过基本推导,求出 w 参数,然后对原问题进行了替换。
[2-1] Rosenblatt, F. (1958). The perceptron: A probabilistic model for information storage and organization in the brain . Psychological Review, 65(6), 386–408.
[2-2] Novikoff, A. B. (1962). On convergence proofs on perceptrons. Symposium on the Mathematical Theory of Automata, 12, 615-622. Polytechnic Institute of Brooklyn.
[2-3] Minsky M L and Papert S A 1969 Perceptrons (Cambridge, MA: MIT Press)
[2-4] Gallant, S. I. (1990). Perceptron-based learning algorithms. IEEE Transactions on Neural Networks, vol. 1, no. 2, pp. 179-191.
[2-5] Freund, Y. and Schapire, R. E. 1998. Large margin classification using the perceptron algorithm. In Proceedings of the 11th Annual Conference on Computational Learning Theory (COLT' 98). ACM Press.
[2-6] Li YY,Zaragoza H,Herbrich R,Shawe-Taylor J,Kandola J. The Perceptron algorithmwith uneven margins. In: Proceedings of the 19th International Conference on MachineLearning. 2002,379–386
[2-7] Widrow, B. , Lehr, M.A., "30 years of Adaptive Neural Networks: Perceptron, Madaline, and Backpropagation, " Proc. IEEE, vol 78, no 9, pp. 1415-1442, (1990)。
[2-8] Cristianini N,Shawe-Taylor J. An Introduction to Support Vector Machines and OtherKernelbased Learning Methods. Cambridge University Press,2000
判别模型
k 近邻法(k-nearest neighbor,k-NN )1968 年由 Cover 和 Hart 提出,是一种基本分类与回归方法。本书只讨论分类问题中的 k 近邻法。
k 近邻法的三个基本要素 :L 2 L_2 L 2 L p L_p L p
模型 :
策略 :y = arg min c j 1 k ∑ x i ∈ N k ( x ) I ( y i ≠ c j ) = 1 − 1 k ∑ x i ∈ N k ( x ) I ( y i = c j ) y = \argmin_{c_j} \frac{1}{k} \sum_{x_i \in N_k(x)} I(y_i \neq c_j) = 1- \frac{1}{k}\sum_{x_i \in N_k(x)} I(y_i = c_j) y = c j arg min k 1 x i ∈ N k ( x ) ∑ I ( y i = c j ) = 1 − k 1 x i ∈ N k ( x ) ∑ I ( y i = c j ) c j c_j c j 1 k ∑ x i ∈ N k ( x ) I ( y i = c j ) \frac{1}{k}\sum_{x_i \in N_k(x)} I(y_i = c_j) k 1 ∑ x i ∈ N k ( x ) I ( y i = c j ) 1 k ∑ x i ∈ N k ( x ) I ( y i ≠ c j ) \frac{1}{k} \sum_{x_i \in N_k(x)} I(y_i \neq c_j) k 1 ∑ x i ∈ N k ( x ) I ( y i = c j ) N k ( x ) N_k(x) N k ( x )
算法 :kd_tree ,ball_tree ,brute(蛮力实现,不算优化,只是把 sklearn 中的参数拿过来),以及其它树结构
下面介绍其中的 kd 树(kd tree 是一个二叉树)方法(kd 树是存储 k 维空间数据的树结构,这里的 k 与 k 近邻法的 k 意义不同)。T = { x 1 , . . . , x N } T = \{x_1,...,x_N\} T = { x 1 , ... , x N } x i x_i x i x i = ( x i ( 1 ) , . . . , x i ( k ) ) T x_i = (x_i^{(1)},...,x_i^{(k)})^T x i = ( x i ( 1 ) , ... , x i ( k ) ) T
function kdtree (list of points pointList, int depth)
{
// Select axis based on depth so that axis cycles through all valid values
var int axis := depth mod k;
// Sort point list and choose median as pivot element
select median by axis from pointList;
// Create node and construct subtree
node.location := median;
node.leftChild := kdtree(points in pointList before median, depth+1);
node.rightChild := kdtree(points in pointList after median, depth+1);
return node;
}
根据第(depth mod k)维查找中位数(中位数所在的点作为节点,第一次就是 root 节点),将数据划分为两个区域,小于中位数的划分在左边,大于中位数的划分在右边
重复 1,depth++
在 kd 树中找出包含目标点 x 的叶结点:从根结点出发,递归地向下访问 kd 树。若目标点 x 当前维的坐标小于切分点的坐标,则移动到左子结点,否则移动到右子结点。直到子结点为叶结点为止。
以此叶结点为“当前最近点”。
递归地向上回退,在每个结点进行以下操作:
当回退到根结点时,搜索结束。最后的“当前最近点”即为 x 的最近邻点。
算法
平均
最差的情况
空间
O ( n ) O(n) O ( n ) O ( n ) O(n) O ( n )
搜索
O ( log n ) O(\log n) O ( log n ) O ( n ) O(n) O ( n )
插入
O ( log n ) O(\log n) O ( log n ) O ( n ) O(n) O ( n )
删除
O ( log n ) O(\log n) O ( log n ) O ( n ) O(n) O ( n )
Distance
sklearn.neighbors.DistanceMetric
Distance computations(scipy.spatial.distance)
24 种距离度量小结
先了解度量空间和赋范空间
实值向量空间的度量:
Euclidean(欧几里得距离也称欧式距离) ∣ ∣ u − v ∣ ∣ 2 {||u-v||}_2 ∣∣ u − v ∣∣ 2 ∑ i ( u i − v i ) 2 \sqrt{\sum_i{(u_i - v_i)^2}} ∑ i ( u i − v i ) 2
SEuclidean(标准化欧几里得距离)
SqEuclidean(平方欧几里得距离)
Mahalanobis(马氏距离) ( u − v ) Σ − 1 ( u − v ) T \sqrt{ (u-v) \Sigma^{-1} (u-v)^T } ( u − v ) Σ − 1 ( u − v ) T
Manhattan/cityblock(城市街区(曼哈顿)距离) ∑ i ∣ u i − v i ∣ \sum_i{|u_i-v_i|} ∑ i ∣ u i − v i ∣
Chebyshev(切比雪夫距离) L ∞ L_\infty L ∞ max i ∣ u i − v i ∣ \max_i{|u_i-v_i|} max i ∣ u i − v i ∣
Minkowski(闵可夫斯基距离) 欧式距离的推广,p=1 时等价于曼哈顿距离,p=2 时等价于欧氏距离,p=∞ 时等价于切比雪夫距离;∑ i ( u i − v i ) p p \sqrt[p]{\sum_i{(u_i - v_i)^p}} p ∑ i ( u i − v i ) p
WMinkowski(加权 Minkowski)
实值向量空间的度量(scipy):
Correlation(皮尔逊相关系数(Pearson Correlation))
Cosine(余弦距离)
JensenShannon(JS 散度也称 JS 距离,是 KL 散度的一种变形)
整数值向量空间的度量:
Hamming(汉明距离)
Canberra(堪培拉距离)
BrayCurtis(布雷柯蒂斯距离)
布尔值向量空间的度量:
Jaccard(Jaccard-Needham 不相似度)
Matching(Hamming 同义词)
Dice(Dice 系数)
Kulsinski(Kulsinski 相异度)
RogersTanimoto(Rogers-Tanimoto 相异度)
RussellRao(Russell-Rao 相异性)
SokalMichener(Sokal-Michener 相异性)
SokalSneath(Sokal-Sneath 相异性)
Yule(scipy 中的 Yule 相异度)
经纬度距离:
Haversine(sklearn 中的半正矢距离)
其它:
[3-1] Cover T,Hart P. Nearest neighbor pattern classification. IEEE Transactions onInformation Theory,1967
[3-2] Hastie T,Tibshirani R,Friedman J. The Elements of Statistical Learning: DataMining,Inference,and Prediction,2001(中译本:统计学习基础——数据挖掘、推理与预测。范明,柴玉梅,昝红英等译。北京:电子工业出版社,2004)
[3-3] Friedman J. Flexible metric nearest neighbor classification. Technical Report,1994
[3-4] Weinberger KQ,Blitzer J,Saul LK. Distance metric learning for large margin nearestneighbor classification. In: Proceedings of the NIPS. 2005
[3-5] Samet H. The Design and Analysis of Spatial Data Structures. Reading,MA: Addison-Wesley,1990
朴素贝叶斯(Naïve Bayes )法是基于贝叶斯定理 与特征条件独立假设 (Naive 天真的)的分类方法。
朴素贝叶斯法是典型的生成学习方法 。生成方法由训练数据学习联合概率分布 P(X,Y),然后求得后验概率分布 P(Y|X)。具体来说,利用训练数据学习 P(X|Y)和 P(Y)的估计,得到联合概率分布:P(X,Y)= P(Y)P(X|Y) ;概率估计方法可以是极大似然估计或贝叶斯估计。
贝叶斯定理(Bayes' theorem) P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B) = \frac{P(B|A)P(A)}{P(B)} P ( A ∣ B ) = P ( B ) P ( B ∣ A ) P ( A )
特征条件独立假设 条件独立 ( A ⊥ B ∣ C ) ⟺ P ( A ∣ B , C ) = P ( A ∣ C ) ( A ⊥ B ∣ C ) ⟺ P ( A , B ∣ C ) = P ( A ∣ C ) P ( B ∣ C ) (A\perp B|C) \iff P(A|B,C) = P(A|C) \\ (A\perp B|C) \iff P(A,B|C) = P(A|C)P(B|C) ( A ⊥ B ∣ C ) ⟺ P ( A ∣ B , C ) = P ( A ∣ C ) ( A ⊥ B ∣ C ) ⟺ P ( A , B ∣ C ) = P ( A ∣ C ) P ( B ∣ C )
特征条件独立假设就是已知 y 的情况下,x 中每个特征相互独立。
数据集T = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } T = \{(x_1,y_1),...,(x_N,y_N)\} T = {( x 1 , y 1 ) , ... , ( x N , y N )} K K K x i x_i x i x i = ( x i ( 1 ) , . . . , x i ( n ) ) T x_i = (x_i^{(1)},...,x_i^{(n)})^T x i = ( x i ( 1 ) , ... , x i ( n ) ) T
模型 :P ( Y = c k ∣ X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) P ( X = x ) ⏟ 贝叶斯定理 ∝ P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) ⏟ 特征条件独立假设 \underbrace{P(Y=c_k|X=x) = \frac{P(X=x|Y=c_k)P(Y=c_k)}{P(X=x)}}_{\text{贝叶斯定理}} \varpropto P(Y=c_k) \underbrace{\prod_j{P(X^{(j)}=x^{(j)}|Y=c_k)}}_{\text{特征条件独立假设}} 贝叶斯定理 P ( Y = c k ∣ X = x ) = P ( X = x ) P ( X = x ∣ Y = c k ) P ( Y = c k ) ∝ P ( Y = c k ) 特征条件独立假设 j ∏ P ( X ( j ) = x ( j ) ∣ Y = c k )
其中P ( X = x ) = ∑ k P ( X = x ∣ Y = c k ) P ( Y = c k ) = ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X=x) = \sum_k{P(X=x|Y=c_k)P(Y=c_k)} = \sum_k{P(Y=c_k) \prod_j{P(X^{(j)}=x^{(j)}|Y=c_k)}} P ( X = x ) = k ∑ P ( X = x ∣ Y = c k ) P ( Y = c k ) = k ∑ P ( Y = c k ) j ∏ P ( X ( j ) = x ( j ) ∣ Y = c k ) c k c_k c k P ( Y = c k ∣ X = x ) ∝ P ( X = x ∣ Y = c k ) P ( Y = c k ) P(Y=c_k|X=x) \varpropto {P(X=x|Y=c_k)P(Y=c_k)} P ( Y = c k ∣ X = x ) ∝ P ( X = x ∣ Y = c k ) P ( Y = c k )
策略 :y = arg max c k P ( Y = c k ∣ X = x ) = arg max c k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) y = \argmax_{c_k} P(Y=c_k|X=x)= \argmax_{c_k}P(Y=c_k)\prod_j{P(X^{(j)}=x^{(j)}|Y=c_k)} y = c k arg max P ( Y = c k ∣ X = x ) = c k arg max P ( Y = c k ) j ∏ P ( X ( j ) = x ( j ) ∣ Y = c k ) arg min y ∑ k = 1 K P ( y ≠ c k ∣ X = x ) = arg min y ( 1 − P ( y = c k ∣ X = x ) ) = arg max y P ( y = c k ∣ X = x ) \argmin_{y}\sum_{k=1}^K P(y \neq c_k|X=x) \\= \argmin_{y}(1- P(y = c_k|X=x)) \\= \argmax_y P(y = c_k|X=x) y arg min k = 1 ∑ K P ( y = c k ∣ X = x ) = y arg min ( 1 − P ( y = c k ∣ X = x )) = y arg max P ( y = c k ∣ X = x )
算法 :参数估计P ( Y = c k ) P(Y=c_k) P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) \prod_j{P(X^{(j)}=x^{(j)}|Y=c_k)} ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) 极大似然估计 :
先验P ( Y = c k ) P(Y=c_k) P ( Y = c k ) P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) N P(Y=c_k) = \frac{\sum_{i=1}^N I(y_i = c_k)}{N} P ( Y = c k ) = N ∑ i = 1 N I ( y i = c k )
第j j j x ( j ) x^{(j)} x ( j ) { a j 1 , . . . , a j S j } \{a_{j1},...,a_{jS_j}\} { a j 1 , ... , a j S j } 注意这里用的都是频率计数,也就是离散特征,如果是连续特征变量,则使用高斯朴素贝叶斯 )P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X^{(j)}=x^{(j)}|Y=c_k) P ( X ( j ) = x ( j ) ∣ Y = c k ) P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) P(X^{(j)} = a_{jl}|Y=c_k) = \frac{\sum_{i=1}^N I(x_i^{(j)} =a_{jl} , y_i = c_k)}{\sum_{i=1}^N I(y_i=c_k)} P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( y i = c k ) ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) j = 1 , 2 , . . . N ; l = 1 , 2... S j ; k = 1 , 2 , . . . K j = 1,2,...N; \quad l=1,2...S_j ;\quad k=1,2,...K j = 1 , 2 , ... N ; l = 1 , 2... S j ; k = 1 , 2 , ... K x i ( j ) x_i^{(j)} x i ( j ) i i i j j j a j l a_{jl} a j l j j j l l l
贝叶斯估计 (smoothed version of maximum likelihood):P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X^{(j)}=x^{(j)}|Y=c_k) P ( X ( j ) = x ( j ) ∣ Y = c k ) j j j x ( j ) = a j S j + 1 x^{(j)} = a_{jS_j+1} x ( j ) = a j S j + 1
注意:朴素贝叶斯法与贝叶斯估计(Bayesian estimation)是不同的概念。
先验P ( Y = c k ) P(Y=c_k) P ( Y = c k ) P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) + λ N + K λ P(Y=c_k) = \frac{\sum_{i=1}^N I(y_i = c_k) + \lambda}{N + K\lambda} P ( Y = c k ) = N + K λ ∑ i = 1 N I ( y i = c k ) + λ
条件概率(likelihood)的贝叶斯估计是:P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) + λ ∑ i = 1 N I ( y i = c k ) + S j λ P(X^{(j)} = a_{jl}|Y=c_k) = \frac{\sum_{i=1}^N I(x_i^{(j)} = a_{jl} , y_i = c_k) + \lambda}{\sum_{i=1}^N I(y_i=c_k) + S_j\lambda} P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( y i = c k ) + S j λ ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) + λ
其中λ ≥ 0 \lambda \geq 0 λ ≥ 0 λ = 0 \lambda = 0 λ = 0 λ = 1 \lambda = 1 λ = 1 Laplacian smoothing );当λ < 1 \lambda < 1 λ < 1
高斯朴素贝叶斯:条件概率(likelihood)P ( X ( j ) = x ( j ) ∣ Y = c k ) = 1 2 π σ j , k 2 e x p ( − ( x ( j ) − μ j , k ) 2 2 σ j , k 2 ) P(X^{(j)} = x^{(j)}|Y=c_k) = \frac{1}{\sqrt{2\pi\sigma_{j,k}^2}} exp\bigg(-\frac{(x^{(j)}-\mu_{j,k})^2}{2\sigma_{j,k}^2}\bigg) P ( X ( j ) = x ( j ) ∣ Y = c k ) = 2 π σ j , k 2 1 e x p ( − 2 σ j , k 2 ( x ( j ) − μ j , k ) 2 ) μ j , k \mu_{j,k} μ j , k c k c_k c k x ( j ) x^{(j)} x ( j ) σ j , k 2 \sigma_{j,k}^2 σ j , k 2 c k c_k c k x ( j ) x^{(j)} x ( j ) P ( Y = c k ) P(Y=c_k) P ( Y = c k ) P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) + λ N + K λ P(Y=c_k) = \frac{\sum_{i=1}^N I(y_i = c_k) + \lambda}{N + K\lambda} P ( Y = c k ) = N + K λ ∑ i = 1 N I ( y i = c k ) + λ
参数估计(Parameter Estimation ) 有点估计(point estimation )和区间估计(interval estimation )两种
点估计法:
极大似然估计(Maximum likelihood estimation, MLE ) 频率学派 观点,它的基本思想是:待估计参数θ \theta θ L ( θ ∣ x ) = f ( x ∣ θ ) = P ( X ∣ θ ) θ ^ M L E = arg max θ L ( θ ∣ x ) L(\theta|x) = f(x|\theta) = P(X|\theta) \\ \hat{\theta}_{MLE} = \argmax_{\theta} L(\theta|x) L ( θ ∣ x ) = f ( x ∣ θ ) = P ( X ∣ θ ) θ ^ M L E = θ arg max L ( θ ∣ x ) P ( X ∣ θ ) P(X|\theta) P ( X ∣ θ ) θ \theta θ c k c_k c k ℓ ( θ ∣ x ) = log L ( θ ∣ x ) \ell(\theta|x) = \log L(\theta|x) ℓ ( θ ∣ x ) = log L ( θ ∣ x )
最大后验估计(maximum a posteriori estimation, MAP ) f ( θ ∣ x ) = f ( x ∣ θ ) g ( θ ) ∫ ϑ f ( x ∣ ϑ ) g ( ϑ ) d ϑ f(\theta|x) = \frac{f(x|\theta)g(\theta)}{\int_\vartheta f(x|\vartheta)g(\vartheta)d\vartheta} f ( θ ∣ x ) = ∫ ϑ f ( x ∣ ϑ ) g ( ϑ ) d ϑ f ( x ∣ θ ) g ( θ ) g g g θ \theta θ θ ^ M A P = arg max θ f ( θ ∣ x ) = arg max θ f ( x ∣ θ ) g ( θ ) ∫ ϑ f ( x ∣ ϑ ) g ( ϑ ) d ϑ = arg max θ f ( x ∣ θ ) g ( θ ) \hat{\theta}_{MAP} = \argmax_{\theta} f(\theta|x) \\= \argmax_{\theta} \frac{f(x|\theta)g(\theta)}{\int_\vartheta f(x|\vartheta)g(\vartheta)d\vartheta} \\= \argmax_{\theta}f(x|\theta)g(\theta) θ ^ M A P = θ arg max f ( θ ∣ x ) = θ arg max ∫ ϑ f ( x ∣ ϑ ) g ( ϑ ) d ϑ f ( x ∣ θ ) g ( θ ) = θ arg max f ( x ∣ θ ) g ( θ ) θ \theta θ θ ^ M A P = arg max θ log f ( x ∣ θ ) g ( θ ) = arg max θ ( log f ( x ∣ θ ) + log g ( θ ) ) \hat{\theta}_{MAP} = \argmax_{\theta}\log{f(x|\theta)g(\theta)} = \argmax_{\theta} (\log{f(x|\theta)} + \log{g(\theta)}) θ ^ M A P = θ arg max log f ( x ∣ θ ) g ( θ ) = θ arg max ( log f ( x ∣ θ ) + log g ( θ ) ) log g ( θ ) \log{g(\theta)} log g ( θ ) 正则化项 ,那么带有正则化项的最大似然学习就可以被解释为 MAP(如:Ridge 回归和 Lasso 回归 )。
最大后验估计就是考虑后验分布极大化而求解参数 的极大似然估计;MAP = 最大似然估计 + 最大似然估计的正则化。
贝叶斯估计(Bayes estimation ) 贝叶斯学派 观点,它的基本思想是:待估计参数 θ \theta θ θ \theta θ 贝叶斯估计需要要计算整个后验概率的概率分布(而 MAP 值需要求解后验分布极大化时的参数θ \theta θ 。
贝叶斯估计和 MAP 挺像的,都是以最大化后验概率为目的。区别在于:
MLE 和 MAP 都是只返回了的预估值
MAP 在计算后验概率的时候,把分母 p(X)给忽略了,在进行贝叶斯估计的时候则不能忽略
贝叶斯估计要计算整个后验概率的概率分布
共轭先验(Conjugate prior ) :如果先验分布 prior 和后验分布 posterior 属于同一分布簇,则 prior 称为 likehood 的共轭先验
最小二乘估计(Least squares estimation, LSE )
矩估计(Method of moments estimators)
区间估计法: confidence intervals (一种频率论方法 )和 可信区间 credible intervals (一种贝叶斯方法 ),此外还有预测区间(Prediction interval )等
采样法: 贝叶斯估计,近似推断Markov chain Monte Carlo, MCMC
[4-1] Mitchell TM. Chapter 1: Generative and discriminative classifiers: Naïve Bayes andlogistic regression. In: Machine Learning. Draft,2005.
[4-2] Hastie T,Tibshirani R,Friedman J. The Elements of Statistical Learning. DataMining,Inference,and Prediction. Springer-Verlag,2001(中译本:统计学习基础——数据挖掘、推理与预测。范明,柴玉梅,昝红英等译。北京:电子工业出版社,2004)
[4-3] Bishop C. Pattern Recognition and Machine Learning ,Springer,2006
判别模型
决策树(decision tree )是一种基本的分类与回归方法,具有良好的可解释性(可视化),通常包括 3 个步骤:特征选择、决策树的生成和决策树的修剪特征选择 :feature_importances_特征重要性,属性越重要,特征空间划分的面积越大)
也就是计算每个特征的(信息增益,基尼指数)来选择特征(作为根节点)进行特征空间划分,注意:划分后再次计算每个特征的(信息增益,基尼指数),除非该特征所在的空间就只有一类了(也就是该特征不可分了,那么就直接生成叶子节点);
特征选择的准则:
决策树的生成 :Decision tree learning 以及Tree algorithms ):
ID3 (Iterative Dichotomiser 3)C4.5 (successor of ID3)CART (Classification And Regression Tree)
决策树的修剪 Decision tree pruning
统计学习方法三要素:
模型 :
策略 :
算法 :
Overview of Decision Trees
Decision Tree
Decision Trees
Entropy, Relative Entropy, Cross Entropy
在信息论中,熵用来衡量一个随机事件的不确定性 。也叫香农熵 Shannon's(人名) entropy。H ( X ) = E p ( x ) [ I ( X ) ] = E p ( x ) [ − log p ( x ) ] = − ∑ i = 1 n p ( x i ) log p ( x i ) = − ∫ X p ( x ) log p ( x ) d x H(X) = E_{p(x)}[I(X)] = E_{p(x)}[-\log {p(x)}] \\= -\sum_{i=1}^n {p(x_i)} \log {p(x_i)} \\= -\int_{X} {p(x)} \log {p(x)} dx H ( X ) = E p ( x ) [ I ( X )] = E p ( x ) [ − log p ( x ) ] = − i = 1 ∑ n p ( x i ) log p ( x i ) = − ∫ X p ( x ) log p ( x ) d x I ( X ) = − log p ( x ) I(X) = -\log {p(x)} I ( X ) = − log p ( x ) 自信息 (Self Information ),是一个随机事件所包含的信息量。一个随机事件发生的概率越高,其自信息越低。如果一个事件必然发生,其自信息为 0。
熵越高,则随机变量的信息越多(不确定性越大,系统越复杂);熵越低,则随机变量的信息越少。
求最大熵:假设概率分布
X
1
2
...
n
p(x)
p₁
p₂
...
pⁿ
max H ( p ) = max − ∑ i = 1 n p i log p i s . t . ∑ i = 1 n p i = 1 \max H(p) = \max -\sum_{i=1}^n p_i \log p_i \\ s.t. \sum_{i=1}^n p_i = 1 max H ( p ) = max − i = 1 ∑ n p i log p i s . t . i = 1 ∑ n p i = 1
由拉格朗日乘数法(Lagrange Multiplier),最大变最小时去掉负号L ( p , λ ) = ∑ i = 1 n p i log p i + λ ( 1 − ∑ i = 1 n p i ) 偏导: ∂ L ∂ p i = log p i + p i . 1 p i − λ 令偏导为 0 得: p i ∗ = e x p ( λ − 1 ) \mathcal L(p,\lambda) = \sum_{i=1}^n p_i \log p_i + \lambda(1-\sum_{i=1}^n p_i) \\偏导:\frac{\partial\mathcal L}{\partial p_i} = \log p_i + p_i.\frac{1}{p_i} - \lambda \\ 令偏导为0得:p_i^*=exp(\lambda-1) L ( p , λ ) = i = 1 ∑ n p i log p i + λ ( 1 − i = 1 ∑ n p i ) 偏导: ∂ p i ∂ L = log p i + p i . p i 1 − λ 令偏导为 0 得: p i ∗ = e x p ( λ − 1 )
因为λ \lambda λ p i ∗ p_i^* p i ∗ p 1 ∗ = p 2 ∗ = . . . = p n ∗ = 1 n p_1^*=p_2^*=...=p_n^*=\frac{1}{n} p 1 ∗ = p 2 ∗ = ... = p n ∗ = n 1
所以概率分布为一个均匀分布,则熵最大 ,由此性质我们来证明熵的取值范围:设 p 是一个均匀分布p = 1 n p = \frac{1}{n} p = n 1 H ( p ) = − ∑ i = 1 n 1 n log 1 n = − ∑ i = 1 n 1 n log n − 1 = ∑ i = 1 n 1 n log n = log n H(p) = -\sum_{i=1}^n \frac{1}{n} \log \frac{1}{n} \\= -\sum_{i=1}^n \frac{1}{n} \log n^{-1} \\= \sum_{i=1}^n \frac{1}{n} \log n \\= \log n H ( p ) = − i = 1 ∑ n n 1 log n 1 = − i = 1 ∑ n n 1 log n − 1 = i = 1 ∑ n n 1 log n = log n 0 ≤ H ( p ) ≤ log n 0 \leq H(p) \leq \log n 0 ≤ H ( p ) ≤ log n
已知连续随机变量的均值为μ \mu μ σ 2 \sigma^2 σ 2 arg max p ( x ) − ∫ p ( x ) log p ( x ) d x s . t . ∫ p ( x ) d x = 1 ∫ x p ( x ) d x = μ ∫ ( x − μ ) 2 p ( x ) d x = σ 2 \argmax_{p(x)} -\int p(x)\log p(x)dx \\ s.t. \int p(x)dx =1 \\ \int xp(x)dx = \mu \\ \int (x-\mu)^2p(x)dx=\sigma^2 p ( x ) arg max − ∫ p ( x ) log p ( x ) d x s . t . ∫ p ( x ) d x = 1 ∫ x p ( x ) d x = μ ∫ ( x − μ ) 2 p ( x ) d x = σ 2 L ( p ( x ) , λ 1 , λ 2 , λ 3 ) = − ∫ p ( x ) log p ( x ) d x + λ 1 ( ∫ p ( x ) d x − 1 ) + λ 2 ( ∫ x p ( x ) d x − μ ) + λ 3 ( ∫ ( x − μ ) 2 p ( x ) d x − σ 2 ) L(p(x),\lambda_1,\lambda_2,\lambda_3) = -\int p(x)\log p(x)dx +\lambda_1(\int p(x)dx - 1)+\lambda_2(\int xp(x)dx - \mu) +\lambda_3(\int (x-\mu)^2p(x)dx - \sigma^2) L ( p ( x ) , λ 1 , λ 2 , λ 3 ) = − ∫ p ( x ) log p ( x ) d x + λ 1 ( ∫ p ( x ) d x − 1 ) + λ 2 ( ∫ x p ( x ) d x − μ ) + λ 3 ( ∫ ( x − μ ) 2 p ( x ) d x − σ 2 ) F ( p ) = ( − log p ( x ) + λ 1 + λ 2 x + λ 3 ( x − μ ) 2 ) p ( x ) F(p)=(-\log p(x) + \lambda_{1} +\lambda_{2}x+ \lambda_{3}(x-\mu)^{2})p(x) F ( p ) = ( − log p ( x ) + λ 1 + λ 2 x + λ 3 ( x − μ ) 2 ) p ( x ) ∂ L ∂ p ( x ) = − [ log p ( x ) + 1 ] + λ 1 + λ 2 x + λ 3 ( x − μ ) 2 \frac{\partial L}{\partial p(x)} = -[\log p(x)+1]+\lambda_1+\lambda_2x+\lambda_3(x-\mu)^2 ∂ p ( x ) ∂ L = − [ log p ( x ) + 1 ] + λ 1 + λ 2 x + λ 3 ( x − μ ) 2 p ( x ) = exp { λ 1 − 1 + λ 2 x + λ 3 ( x − μ ) 2 } p(x) = \exp\{\lambda_1-1+\lambda_2x+\lambda_3(x-\mu)^2\} p ( x ) = exp { λ 1 − 1 + λ 2 x + λ 3 ( x − μ ) 2 } p ( x ) = exp { λ 1 − 1 + λ 2 x + λ 3 ( x − μ ) 2 } = e − 1 + λ 1 ⋅ e λ 2 x + λ 3 ( x − μ ) 2 = C e λ 2 x + λ 3 ( x − μ ) 2 = C e λ 3 ( x 2 − 2 ( μ − λ 2 2 λ 3 ) x + u 2 ) = C e λ 3 ( x − μ + λ 2 2 λ 3 ) 2 = C . exp { λ 3 ( x − μ + λ 2 2 λ 3 ) 2 } p(x) = \exp\{\lambda_1-1+\lambda_2x+\lambda_3(x-\mu)^2\}\\ =e^{-1+\lambda_{1}}\cdot e^{\lambda_{2}x+ \lambda_{3}(x-\mu)^{2}}=C e^{\lambda_{2}x+ \lambda_{3}(x-\mu)^{2}} \\ = Ce^{\lambda_{3}(x^{2} -2(\mu-\frac{\lambda_{2}}{2\lambda_{3}})x+ u^{2})} = C e^{\lambda_{3}(x -\mu+ \frac{\lambda_{2}}{2\lambda_{3}})^{2}} \\= C.\exp\{\lambda_3(x-\mu+\frac{\lambda_2}{2\lambda_3})^2\} p ( x ) = exp { λ 1 − 1 + λ 2 x + λ 3 ( x − μ ) 2 } = e − 1 + λ 1 ⋅ e λ 2 x + λ 3 ( x − μ ) 2 = C e λ 2 x + λ 3 ( x − μ ) 2 = C e λ 3 ( x 2 − 2 ( μ − 2 λ 3 λ 2 ) x + u 2 ) = C e λ 3 ( x − μ + 2 λ 3 λ 2 ) 2 = C . exp { λ 3 ( x − μ + 2 λ 3 λ 2 ) 2 }
根据( x − μ + λ 2 2 λ 3 ) 2 (x-\mu+\frac{\lambda_2}{2\lambda_3})^2 ( x − μ + 2 λ 3 λ 2 ) 2 p ( x ) p(x) p ( x ) μ − λ 2 2 λ 3 \mu - \frac{\lambda_{2}}{2\lambda_{3}} μ − 2 λ 3 λ 2 p ( x ) = p ( − x ) p(x) = p(-x) p ( x ) = p ( − x ) E [ p ( x ) ] = μ − λ 2 2 λ 3 = μ E[p(x)] = \mu - \frac{\lambda_{2}}{2\lambda_{3}} = \mu E [ p ( x )] = μ − 2 λ 3 λ 2 = μ λ 2 = 0 \lambda_{2} = 0 λ 2 = 0
那么p ( x ) = C e λ 3 ( x − μ ) 2 p(x)= C e^{\lambda_{3}(x -\mu)^{2}} p ( x ) = C e λ 3 ( x − μ ) 2 p ( x ) > 0 p(x)>0 p ( x ) > 0 C > 0 , λ 3 < 0 C>0,\lambda_{3}<0 C > 0 , λ 3 < 0 λ = − λ 3 \lambda = -\lambda_3 λ = − λ 3 ∫ e − x 2 2 d x = 2 π \int e^{-\frac{x^2}{2}}dx = \sqrt{2\pi} ∫ e − 2 x 2 d x = 2 π ∫ p ( x ) d x = 1 = C ∫ e − λ ( x − μ ) 2 d x = C π λ \int p(x)dx = 1 = C\int e^{-\lambda(x -\mu)^{2}} dx = C\sqrt{\frac{\pi}{\lambda}} ∫ p ( x ) d x = 1 = C ∫ e − λ ( x − μ ) 2 d x = C λ π C = λ π C = \sqrt{\frac{\lambda}{\pi}} C = π λ ∫ ( x − μ ) 2 p ( x ) d x = σ 2 = ∫ ( x − μ ) 2 e − λ ( x − μ ) 2 d x = C π λ . 1 2 λ = 1 2 λ \int (x-\mu)^2p(x)dx=\sigma^2 = \int (x-\mu)^2e^{-\lambda(x -\mu)^{2}}dx = C\sqrt{\frac{\pi}{\lambda}}.\frac{1}{2\lambda} = \frac{1}{2\lambda} ∫ ( x − μ ) 2 p ( x ) d x = σ 2 = ∫ ( x − μ ) 2 e − λ ( x − μ ) 2 d x = C λ π . 2 λ 1 = 2 λ 1 λ 3 = − 1 2 σ 2 \lambda_3 = -\frac{1}{2\sigma^2} λ 3 = − 2 σ 2 1 C = λ π = 1 2 π σ 2 C = \sqrt{\frac{\lambda}{\pi}} = \sqrt{\frac{1}{2\pi\sigma^2}} C = π λ = 2 π σ 2 1 p ( x ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 p(x) = \sqrt{\frac{1}{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} p ( x ) = 2 π σ 2 1 e − 2 σ 2 ( x − μ ) 2
X X X Y Y Y 联合熵 (Joint Entropy )为:H ( X , Y ) = − ∑ x ∈ X ∑ y ∈ Y P ( x , y ) log 2 [ P ( x , y ) ] = E X , Y [ − log p ( x , y ) ] = − ∑ x , y p ( x , y ) log p ( x , y ) {\displaystyle \mathrm {H} (X,Y)=-\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}P(x,y)\log _{2}[P(x,y)]} \\=\mathbb {E} _{X,Y}[-\log p(x,y)]=-\sum _{x,y}p(x,y)\log p(x ,y)\, H ( X , Y ) = − x ∈ X ∑ y ∈ Y ∑ P ( x , y ) log 2 [ P ( x , y )] = E X , Y [ − log p ( x , y )] = − x , y ∑ p ( x , y ) log p ( x , y )
积分形式(连续):h ( X , Y ) = − ∫ X , Y f ( x , y ) log f ( x , y ) d x d y {\displaystyle h(X,Y)=-\int _{{\mathcal {X}},{\mathcal {Y}}}f(x,y)\log f(x,y)\,dxdy} h ( X , Y ) = − ∫ X , Y f ( x , y ) log f ( x , y ) d x d y
多个随机变量:H ( X 1 , . . . , X n ) = − ∑ x 1 ∈ X 1 . . . ∑ x n ∈ X n P ( x 1 , . . . , x n ) log 2 [ P ( x 1 , . . . , x n ) ] {\displaystyle \mathrm {H} (X_{1},...,X_{n})=-\sum _{x_{1}\in {\mathcal {X}}_{1}}...\sum _{x_{n}\in {\mathcal {X}}_{n}}P(x_{1},...,x_{n})\log _{2}[P(x_{1},...,x_{n})]} H ( X 1 , ... , X n ) = − x 1 ∈ X 1 ∑ ... x n ∈ X n ∑ P ( x 1 , ... , x n ) log 2 [ P ( x 1 , ... , x n )] h ( X 1 , … , X n ) = − ∫ f ( x 1 , … , x n ) log f ( x 1 , … , x n ) d x 1 … d x n {\displaystyle h(X_{1},\ldots ,X_{n})=-\int f(x_{1},\ldots ,x_{n})\log f(x_{1},\ldots ,x_{n})\,dx_{1}\ldots dx_{n}} h ( X 1 , … , X n ) = − ∫ f ( x 1 , … , x n ) log f ( x 1 , … , x n ) d x 1 … d x n
X X X Y Y Y 条件熵 (Conditional Entropy )为:
H ( Y ∣ X ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) log p ( x , y ) p ( x ) {\displaystyle \mathrm {H} (Y|X)\ =-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log {\frac {p(x,y)}{p(x)}}} H ( Y ∣ X ) = − x ∈ X , y ∈ Y ∑ p ( x , y ) log p ( x ) p ( x , y )
证明:H ( Y ∣ X ) ≡ ∑ x ∈ X p ( x ) H ( Y ∣ X = x ) = − ∑ x ∈ X p ( x ) ∑ y ∈ Y p ( y ∣ x ) log p ( y ∣ x ) = − ∑ x ∈ X ∑ y ∈ Y p ( x , y ) log p ( y ∣ x ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) log p ( y ∣ x ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) log p ( x , y ) p ( x ) . = ∑ x ∈ X , y ∈ Y p ( x , y ) log p ( x ) p ( x , y ) . {\displaystyle {\begin{aligned}\mathrm {H} (Y|X)\ &\equiv \sum _{x\in {\mathcal {X}}}\,p(x)\,\mathrm {H} (Y|X=x)\\&=-\sum _{x\in {\mathcal {X}}}p(x)\sum _{y\in {\mathcal {Y}}}\,p(y|x)\,\log \,p(y|x)\\&=-\sum _{x\in {\mathcal {X}}}\sum _{y\in {\mathcal {Y}}}\,p(x,y)\,\log \,p(y|x)\\&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log \,p(y|x)\\&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log {\frac {p(x,y)}{p(x)}}.\\&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log {\frac {p(x)}{p(x,y)}}.\\\end{aligned}}} H ( Y ∣ X ) ≡ x ∈ X ∑ p ( x ) H ( Y ∣ X = x ) = − x ∈ X ∑ p ( x ) y ∈ Y ∑ p ( y ∣ x ) log p ( y ∣ x ) = − x ∈ X ∑ y ∈ Y ∑ p ( x , y ) log p ( y ∣ x ) = − x ∈ X , y ∈ Y ∑ p ( x , y ) log p ( y ∣ x ) = − x ∈ X , y ∈ Y ∑ p ( x , y ) log p ( x ) p ( x , y ) . = x ∈ X , y ∈ Y ∑ p ( x , y ) log p ( x , y ) p ( x ) .
积分形式(连续):h ( X ∣ Y ) = − ∫ X , Y f ( x , y ) log f ( x ∣ y ) d x d y {\displaystyle h(X|Y)=-\int _{{\mathcal {X}},{\mathcal {Y}}}f(x,y)\log f(x|y)\,dxdy} h ( X ∣ Y ) = − ∫ X , Y f ( x , y ) log f ( x ∣ y ) d x d y
根据定义写作:H ( Y ∣ X ) = H ( X , Y ) − H ( X ) {\displaystyle \mathrm {H} (Y|X)\,=\,\mathrm {H} (X,Y)-\mathrm {H} (X)} H ( Y ∣ X ) = H ( X , Y ) − H ( X ) H ( X 1 , X 2 , … , X n ) = ∑ i = 1 n H ( X i ∣ X 1 , … , X i − 1 ) {\displaystyle \mathrm {H} (X_{1},X_{2},\ldots ,X_{n})=\sum _{i=1}^{n}\mathrm {H} (X_{i}|X_{1},\ldots ,X_{i-1})} H ( X 1 , X 2 , … , X n ) = i = 1 ∑ n H ( X i ∣ X 1 , … , X i − 1 )
证明:H ( Y ∣ X ) = ∑ x ∈ X , y ∈ Y p ( x , y ) log ( p ( x ) p ( x , y ) ) = ∑ x ∈ X , y ∈ Y p ( x , y ) ( log ( p ( x ) ) − log ( p ( x , y ) ) ) = − ∑ x ∈ X , y ∈ Y p ( x , y ) log ( p ( x , y ) ) + ∑ x ∈ X , y ∈ Y p ( x , y ) log ( p ( x ) ) = H ( X , Y ) + ∑ x ∈ X p ( x ) log ( p ( x ) ) = H ( X , Y ) − H ( X ) . {\displaystyle {\begin{aligned}\mathrm {H} (Y|X)&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log \left({\frac {p(x)}{p(x,y)}}\right)\\[4pt]&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)(\log(p(x))-\log(p(x,y)))\\[4pt]&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log(p(x,y))+\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}{p(x,y)\log(p(x))}\\[4pt]&=\mathrm {H} (X,Y)+\sum _{x\in {\mathcal {X}}}p(x)\log(p(x))\\[4pt]&=\mathrm {H} (X,Y)-\mathrm {H} (X).\end{aligned}}} H ( Y ∣ X ) = x ∈ X , y ∈ Y ∑ p ( x , y ) log ( p ( x , y ) p ( x ) ) = x ∈ X , y ∈ Y ∑ p ( x , y ) ( log ( p ( x )) − log ( p ( x , y ))) = − x ∈ X , y ∈ Y ∑ p ( x , y ) log ( p ( x , y )) + x ∈ X , y ∈ Y ∑ p ( x , y ) log ( p ( x )) = H ( X , Y ) + x ∈ X ∑ p ( x ) log ( p ( x )) = H ( X , Y ) − H ( X ) .
如果变量 𝑋 和 𝑌 互相独立,它们的互信息为零.
I ( X ; Y ) = E X , Y [ S I ( x , y ) ] = ∑ x , y p ( x , y ) log p ( x , y ) p ( x ) p ( y ) I(X;Y)=\mathbb {E} _{X,Y}[SI(x,y)]=\sum _{x,y}p(x,y)\log {\frac {p(x,y)}{p(x)\,p(y)}} I ( X ; Y ) = E X , Y [ S I ( x , y )] = x , y ∑ p ( x , y ) log p ( x ) p ( y ) p ( x , y ) pointwise mutual information
基本性质:I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) . I(X;Y)=H(X)-H(X|Y) =H(Y)- H(Y|X).\, I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) . I ( X ; Y ) = I ( Y ; X ) = H ( X ) + H ( Y ) − H ( X , Y ) . I(X;Y)=I(Y;X)=H(X)+H(Y)-H(X,Y).\, I ( X ; Y ) = I ( Y ; X ) = H ( X ) + H ( Y ) − H ( X , Y ) .
互信息可以表示为给定 Y 值的 X 的后验概率分布 与 X 的先验分布之间的平均 Kullback-Leibler 散度:I ( X ; Y ) = E p ( y ) [ D K L ( p ( X ∣ Y = y ) ∥ p ( X ) ) ] . I(X;Y)=\mathbb {E} _{p(y)}[D_{\mathrm {KL} }(p(X|Y=y)\|p(X))]. I ( X ; Y ) = E p ( y ) [ D KL ( p ( X ∣ Y = y ) ∥ p ( X ))] . I ( X ; Y ) = D K L ( p ( X , Y ) ∥ p ( X ) p ( Y ) ) . I(X;Y)=D_{\mathrm {KL} }(p(X,Y)\|p(X)p(Y)). I ( X ; Y ) = D KL ( p ( X , Y ) ∥ p ( X ) p ( Y )) .
统计学习方法中讲到 信息增益等价互信息(74 页),而维基百科中信息增益是Kullback-Leibler 散度
在给定 分布 𝑝 的情况下,如果 分布 𝑞 和 分布 𝑝 越接近,交叉熵越小;如果 分布 𝑞 和 分布 𝑝 越远,交叉H ( p , q ) = − E p [ log q ] = − ∑ x ∈ X p ( x ) log q ( x ) = H ( p ) + D K L ( p ∥ q ) {\displaystyle H(p,q)=-\operatorname {E} _{p}[\log q]} =-\sum _{x\in {\mathcal {X}}}p(x)\,\log q(x) = H(p)+D_{\mathrm {KL} }(p\|q) H ( p , q ) = − E p [ log q ] = − x ∈ X ∑ p ( x ) log q ( x ) = H ( p ) + D KL ( p ∥ q )
注意与联合熵H ( X , Y ) {H} (X,Y) H ( X , Y ) H ( p , q ) H(p,q) H ( p , q ) H q ( p ) H_q(p) H q ( p ) Difference of notation between cross entropy and joint entropy 以及Relation between cross entropy and joint entropy
KL 散度(Kullback-Leibler Divergence),也叫 KL 距离或相对熵(Relative Entropy),是用概率分布 𝑞 来近似 𝑝 时所造成的信息损失量,KL 散度总是大于等于 0 的。可以衡量两个概率分布之间的距离 .KL 散度只有当 𝑝 = 𝑞 时,KL(𝑝, 𝑞) = 0.如果两个分布越接近,KL 散度越小;如果两个分布越远,KL 散度就越大.但 KL 散度并不是一个真正的度量或距离,一是 KL 散度不满足距离的对称性,二是 KL 散度不满足距离的三角不等式性质.
D K L ( p ( X ) ∥ q ( X ) ) = ∑ x ∈ X − p ( x ) log q ( x ) − ∑ x ∈ X − p ( x ) log p ( x ) = ∑ x ∈ X p ( x ) log p ( x ) q ( x ) = − ∑ x ∈ X p ( x ) log q ( x ) p ( x ) . D_{\mathrm {KL} }(p(X)\|q(X))=\sum _{x\in X}-p(x)\log {q(x)}\,-\,\sum _{x\in X}-p(x)\log {p(x)} \\=\sum _{x\in X}p(x)\log {\frac {p(x)}{q(x)}} = -\sum _{x\in X}p(x)\log {\frac {q(x)}{p(x)}}. D KL ( p ( X ) ∥ q ( X )) = x ∈ X ∑ − p ( x ) log q ( x ) − x ∈ X ∑ − p ( x ) log p ( x ) = x ∈ X ∑ p ( x ) log q ( x ) p ( x ) = − x ∈ X ∑ p ( x ) log p ( x ) q ( x ) . K L ( p , q ) , K L ( p ∣ q ) , K L ( p ∥ q ) , D K L ( p , q ) KL(p,q) , KL(p|q) , KL(p\|q) , D_{KL}(p,q) K L ( p , q ) , K L ( p ∣ q ) , K L ( p ∥ q ) , D K L ( p , q )
应用:如:变分推断
JS 散度(Jensen-Shannon Divergence)是一种对称的衡量两个分布相似度的度量方式,是 KL 散度一种改进.但两种散度都存在一个问题,即如果两个分布 𝑝, 𝑞 没有重叠或者重叠非常少时,KL 散度和 JS 散度都很难衡量两个分布的距离.
D J S ( P ∥ Q ) = 1 2 D K L ( P ∥ M ) + 1 2 D K L ( Q ∥ M ) {{\rm {D}_{JS}}}(P\parallel Q)={\frac {1}{2}}D_{KL}(P\parallel M)+{\frac {1}{2}}D_{KL}(Q\parallel M) D JS ( P ∥ Q ) = 2 1 D K L ( P ∥ M ) + 2 1 D K L ( Q ∥ M ) M = 1 2 ( P + Q ) M={\frac {1}{2}}(P+Q) M = 2 1 ( P + Q ) J S D ( P ∥ Q ) , J S ( P ∥ Q ) , J S ( P , Q ) JSD(P\|Q), JS(P\|Q) ,JS(P,Q) J S D ( P ∥ Q ) , J S ( P ∥ Q ) , J S ( P , Q )
属于一种统计距离(Statistical distance )
统计距离还有Wasserstein 距离 Wasserstein distance ,也用于衡量两个分布之间的距μ , ν , p t h − W a s s e r s t e i n \mu ,\nu,p^{th}-Wasserstein μ , ν , p t h − Wa ssers t e in
W p ( μ , ν ) : = ( inf γ ∈ Γ ( μ , ν ) ∫ M × M d ( x , y ) p d γ ( x , y ) ) 1 / p , {\displaystyle W_{p}(\mu ,\nu ):=\left(\inf _{\gamma \in \Gamma (\mu ,\nu )}\int _{M\times M}d(x,y)^{p}\,\mathrm {d} \gamma (x,y)\right)^{1/p},} W p ( μ , ν ) := ( γ ∈ Γ ( μ , ν ) inf ∫ M × M d ( x , y ) p d γ ( x , y ) ) 1/ p ,
Wasserstein 距离相比 KL 散度和 JS 散度的优势在于:即使两个分布没有重叠或者重叠非常少,Wasserstein 距离仍然能反映两个分布的远近.参见pdf443 页附录
[5-1] Olshen R A, Quinlan J R. Induction of decision trees . Machine Learning,1986,1(1): 81–106
[5-2] Olshen R A, Quinlan J R. C4. 5: Programs for Machine Learning . Morgan Kaufmann,1992
[5-3] Olshen R A, Breiman L,Friedman J,Stone C. Classification and Regression Trees. Wadsworth,1984
[5-4] Ripley B. Pattern Recognition and Neural Networks. Cambridge UniversityPress,1996
[5-5] Liu B. Web Data Mining: Exploring Hyperlinks,Contents and Usage Data. Springer-Verlag,2006
[5-6] Hyafil L,Rivest R L. Constructing Optimal Binary Decision Trees is NP-complete.Information Processing Letters,1976,5(1): 15–17
[5-7] Hastie T,Tibshirani R,Friedman JH. The Elements of Statistical Learning: DataMining,Inference,and Prediction . New York: Springer-Verlag,2001
[5-8] Yamanishi K. A learning criterion for stochastic rules. Machine Learning,1992
[5-9] Li H,Yamanishi K. Text classification using ESC-based stochastic decision lists.Information Processing & Management,2002,38(3): 343–361
逻辑斯谛回归 (logistic regression )(也有称 对数几率回归)是统计学习中的经典分类方法。最大熵是概率模型学习的一个准则,将其推广到分类问题得到最大熵模型 (maximum entropy model )。逻辑斯谛回归模型与最大熵模型都属于对数线性模型 (也有称最大熵分类或对数线性分类,所以这里的模型都是分类模型)。
一个事件的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是 p,那么该事件的几率是p 1 − p \frac{p}{1-p} 1 − p p 对数几率 (log odds)或 logit 函数是:l o g i t ( p ) = log p 1 − p (6-1) logit(p) = \log\frac{p}{1-p} \label{6-1}\tag{6-1} l o g i t ( p ) = log 1 − p p ( 6-1 )
模型 :P ( Y = 1 ∣ x ) = exp ( w . x ) 1 + exp ( w . x ) = σ ( w . x ) P ( Y = 0 ∣ x ) = 1 1 + exp ( w . x ) = 1 − σ ( w . x ) (6-2) P(Y=1|x) = \frac{\exp{(w.x)}}{1+\exp{(w.x)}} = \sigma{(w.x)} \\ P(Y=0|x) = \frac{1}{1+\exp{(w.x)}} = 1 - \sigma{(w.x)} \label{6-2}\tag{6-2} P ( Y = 1∣ x ) = 1 + exp ( w . x ) exp ( w . x ) = σ ( w . x ) P ( Y = 0∣ x ) = 1 + exp ( w . x ) 1 = 1 − σ ( w . x ) ( 6-2 )
该事件的对数几率:log P ( Y = 1 ∣ x ) 1 − P ( Y = 1 ∣ x ) = w . x \log\frac{P(Y=1|x)}{1-P(Y=1|x)} = w.x log 1 − P ( Y = 1∣ x ) P ( Y = 1∣ x ) = w . x
策略 :T = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } , x i ∈ R n , y i ∈ { 0 , 1 } T=\{(x_1,y_1),...,(x_N,y_N)\} , x_i \in \mathbb{R}^n , y_i \in \{0,1\} T = {( x 1 , y 1 ) , ... , ( x N , y N )} , x i ∈ R n , y i ∈ { 0 , 1 } [ σ ( w . x i ) ] y i [ 1 − σ ( w . x i ) ] 1 − y i [\sigma{(w.x_i)}]^{y_i}[1-\sigma{(w.x_i)}]^{1-y_i} [ σ ( w . x i ) ] y i [ 1 − σ ( w . x i ) ] 1 − y i L ( w ∣ y ; x ) = P ( Y ∣ X ; w ) = ∏ i = 1 N P ( y i ∣ x i ; w ) = ∏ i = 1 N [ σ ( w . x i ) ] y i [ 1 − σ ( w . x i ) ] 1 − y i L(w|y;x) = P(Y|X;w) = \prod_{i=1}^N P(y_i|x_i;w)= \prod_{i=1}^N [\sigma{(w.x_i)}]^{y_i}[1-\sigma{(w.x_i)}]^{1-y_i} L ( w ∣ y ; x ) = P ( Y ∣ X ; w ) = i = 1 ∏ N P ( y i ∣ x i ; w ) = i = 1 ∏ N [ σ ( w . x i ) ] y i [ 1 − σ ( w . x i ) ] 1 − y i
log likelihood(maximized):log L ( w ∣ y ; x ) = ∑ i = 1 N [ y i log σ ( w . x i ) + ( 1 − y i ) log ( 1 − σ ( w . x i ) ) ] \log {L(w|y;x)} = \sum_{i=1}^N[y_i\log\sigma{(w.x_i)} + (1-y_i)\log(1-\sigma{(w.x_i)})] log L ( w ∣ y ; x ) = i = 1 ∑ N [ y i log σ ( w . x i ) + ( 1 − y i ) log ( 1 − σ ( w . x i ) )]
negative log likelihood(minimize):− log L ( w ∣ y ; x ) -\log {L(w|y;x)} − log L ( w ∣ y ; x )
算法 :
极大似然估计 MLE(Maximum Likelihood Estimation)w ∗ = arg min w − log L ( w ∣ y ; x ) w^* = \argmin_w -\log {L(w|y;x)} w ∗ = w arg min − log L ( w ∣ y ; x )
然后使用随机梯度下降法(Stochastic Gradient Descent)求最优值处的参数
sklearn 中代价函数 y ∈ { − 1 , + 1 } y \in \{-1,+1\} y ∈ { − 1 , + 1 } P ( Y = + 1 ∣ x ) = exp ( w . x ) 1 + exp ( w . x ) = σ ( w . x ) P ( Y = − 1 ∣ x ) = 1 1 + exp ( w . x ) = 1 − σ ( w . x ) = σ ( − w . x ) P(Y=+1|x) = \frac{\exp{(w.x)}}{1+\exp{(w.x)}} = \sigma{(w.x)} \\ P(Y=-1|x) = \frac{1}{1+\exp{(w.x)}} = 1 - \sigma{(w.x)} = \sigma{(-w.x)} P ( Y = + 1∣ x ) = 1 + exp ( w . x ) exp ( w . x ) = σ ( w . x ) P ( Y = − 1∣ x ) = 1 + exp ( w . x ) 1 = 1 − σ ( w . x ) = σ ( − w . x ) σ ( y i . w . x i ) \sigma{(y_i.w.x_i)} σ ( y i . w . x i )
− log ∏ i = 1 N σ ( y i . w . x i ) = ∑ i = 1 N − log σ ( y i . w . x i ) = ∑ i = 1 N log 1 σ ( y i . w . x i ) = ∑ i = 1 N log 1 exp ( y i . w . x i ) 1 + exp ( y i . w . x i ) = ∑ i = 1 N log ( 1 + 1 exp ( y i . w . x i ) ) = ∑ i = 1 N log ( 1 + exp ( − y i . w . x i ) ) -\log\prod_{i=1}^N \sigma{(y_i.w.x_i)} = \sum_{i=1}^N-\log\sigma{(y_i.w.x_i)}= \sum_{i=1}^N \log\frac{1}{\sigma{(y_i.w.x_i)}} \\=
\sum_{i=1}^N \log\frac{1}{\frac{\exp{(y_i.w.x_i)}}{1+\exp{(y_i.w.x_i)}}}\\= \sum_{i=1}^N \log(1+\frac{1}{\exp{(y_i.w.x_i)}})\\= \sum_{i=1}^N \log(1+\exp{(-y_i.w.x_i)}) − log i = 1 ∏ N σ ( y i . w . x i ) = i = 1 ∑ N − log σ ( y i . w . x i ) = i = 1 ∑ N log σ ( y i . w . x i ) 1 = i = 1 ∑ N log 1 + e x p ( y i . w . x i ) e x p ( y i . w . x i ) 1 = i = 1 ∑ N log ( 1 + exp ( y i . w . x i ) 1 ) = i = 1 ∑ N log ( 1 + exp ( − y i . w . x i ) )
当然 sklearn 中加入的正则项。
Softmax 回归是 Logistic 回归的多分类情况。
逻辑斯蒂回归模型的思想跟线性回归模型思想不一样,线性回归模型思想是最小化真实值与模型预测值的误差,而逻辑斯蒂回归模型思想就比较狠了,预测值预测对了损失函数就是 0,错了损失就是无穷大,我个人的理解(一般采用的是-log(h(x)) 这是一个凸函数,刚好满足要求)
熵的概念在统计学习与机器学习中真是很重要,最大熵模型(maximum entropy model )是概率模型学习中一个准则,其思想为:在学习概率模型时,所有可能的模型中熵最大的模型是最好的模型;若概率模型需要满足一些约束,则最大熵原理(Principle of maximum entropy)就是在满足已知约束的条件集合中选择熵最大模型。
均值和方差也被称为一阶矩和二阶矩(二至四阶中心矩被定义为方差(variance)、偏度(skewness)和峰度(kurtosis))证明 )证明 过)
模型 :h ( X ) = − ∫ p ( x ) log p ( x ) d x h(X) = - \int p(x)\log p(x) dx h ( X ) = − ∫ p ( x ) log p ( x ) d x
策略 :Maximize p h ( p ) = − ∫ S p ( x ) log p ( x ) d x Subject to ∫ S p ( x ) d x = 1 p ( x ) ≥ 0 ∫ S p ( x ) f i ( x ) d x = α i , i = 1 , 2 , 3 , … , n \begin{array}{ll}
&\underset{p}{\text{Maximize}} & \displaystyle h(p) = - \int_S p(x)\log p(x) dx \\
&\text{Subject to} &\displaystyle \int_S p(x) dx = 1 \\[2pt]
&~ & p(x) \ge 0 \\[2pt]
&~ & \displaystyle \int_S p(x) f_i(x) dx = \alpha_i, ~i=1,2,3,\dots,n
\end{array} p Maximize Subject to h ( p ) = − ∫ S p ( x ) log p ( x ) d x ∫ S p ( x ) d x = 1 p ( x ) ≥ 0 ∫ S p ( x ) f i ( x ) d x = α i , i = 1 , 2 , 3 , … , n 矩约束 (均值和方差也被称为一阶矩和二阶矩),在模型中有时会假设随机变量的矩为常数),并且能够使得熵最大。将上述优化问题写成标准形式:Minimize p ∫ S p ( x ) log p ( x ) d x Subject to − p ( x ) ≤ 0 ∫ S p ( x ) d x = 1 ∫ S p ( x ) f i ( x ) d x = α i , i = 1 , 2 , 3 , … , n \begin{array}{ll}
&\underset{p}{\text{Minimize}} & \displaystyle \int_S p(x)\log p(x) dx \\
&\text{Subject to} &-p(x) \le 0 \\[2pt]
&~ &\displaystyle \int_S p(x) dx = 1 \\
&~ & \displaystyle \int_S p(x) f_i(x) dx = \alpha_i, ~i=1,2,3,\dots,n
\end{array} p Minimize Subject to ∫ S p ( x ) log p ( x ) d x − p ( x ) ≤ 0 ∫ S p ( x ) d x = 1 ∫ S p ( x ) f i ( x ) d x = α i , i = 1 , 2 , 3 , … , n
算法 :L ( p , λ ) = ∫ S p log p d x − μ − 1 p + μ 0 ( ∫ S p d x − 1 ) + ∑ j = 1 n λ j ( ∫ S p f j d x − α j ) L(p,\boldsymbol{\lambda}) = \int_S p\log p ~dx - \mu_{-1}p + \mu_0 \left(\int_S p ~dx - 1\right) + \sum_{j=1}^n \lambda_j \left(\int_S pf_j~dx - \alpha_j\right) L ( p , λ ) = ∫ S p log p d x − μ − 1 p + μ 0 ( ∫ S p d x − 1 ) + j = 1 ∑ n λ j ( ∫ S p f j d x − α j ) ∂ L ∂ p = ln p + 1 − μ − 1 + μ 0 + ∑ j = 1 n λ j f j : = 0 ⟹ p = exp ( − 1 + μ − 1 − μ 0 − ∑ j = 1 n λ j f j ) = c ∗ e − ∑ j = 1 n λ j ∗ f j ( x ) : = p ∗ \begin{gathered}
\frac{\partial L}{\partial p} = \ln p + 1 - \mu_{-1} + \mu_0 + \sum_{j=1}^n \lambda_jf_j := 0 \\
\implies p = \exp\left(-1 + \mu_{-1} - \mu_0 - \sum_{j=1}^n \lambda_j f_j \right) =\displaystyle c^* e^{-\sum_{j=1}^n\lambda_j^* f_j(x)} := p^*
\end{gathered} ∂ p ∂ L = ln p + 1 − μ − 1 + μ 0 + j = 1 ∑ n λ j f j := 0 ⟹ p = exp ( − 1 + μ − 1 − μ 0 − j = 1 ∑ n λ j f j ) = c ∗ e − ∑ j = 1 n λ j ∗ f j ( x ) := p ∗
逻辑回归(非常详细) 机器学习实现与分析之四(广义线性模型)
逻辑回归——Logistic 的起源 Logistic 回归的起源(上) Logistic 回归的起源(中) Logistic 回归的起源(下)
6.2 Logistic Regression and the Cross Entropy Cost - Logistic regression - y 属于 0 或 1
6.3 Logistic Regression and the Softmax Cost-Logistic regression sklearn 中的代价函数,这里的 y 属于-1 或 1
Generalized Linear Models (GLM)
Generalized Linear Models
Generalized Linear Models Explained with Examples
Generalized Linear Model Theory - 推荐
Generalized Linear Models
在线性回归模型中的假设中,有两点需要提出:
假设因变量服从高斯分布:Y = θ T x + ξ Y={{\theta }^{T}}x+\xi Y = θ T x + ξ ξ ∼ N ( 0 , σ 2 ) \xi \sim N(0,{{\sigma }^{2}}) ξ ∼ N ( 0 , σ 2 ) Y ∼ N ( θ T x , σ 2 ) Y\sim N({{\theta }^{T}}x,{{\sigma }^{2}}) Y ∼ N ( θ T x , σ 2 )
模型预测的输出为E [ Y ] E[Y] E [ Y ] Y = θ T x + ξ Y={{\theta }^{T}}x+\xi Y = θ T x + ξ E [ Y ] = E [ θ T x + ξ ] = θ T x E[Y]=E[{{\theta }^{T}}x+\xi ]={{\theta }^{T}}x E [ Y ] = E [ θ T x + ξ ] = θ T x η = θ T x \eta ={{\theta }^{T}}x η = θ T x η = E [ Y ] \eta =E[Y] η = E [ Y ]
广义线性模型可以认为在以上两点假设做了扩展:
因变量分布不一定是高斯分布,服从一个指数分布族(Exponential family )即可。
模型预测输出仍然可以认为是E [ Y ] E[Y] E [ Y ] E [ T ( Y ) ] E[T(Y)] E [ T ( Y )] T ( Y ) = Y T(Y)=Y T ( Y ) = Y Y Y Y E [ Y ] E[Y] E [ Y ] η = θ T x \eta ={{\theta }^{T}}x η = θ T x η = g ( E [ Y ] ) \eta =g(E[Y]) η = g ( E [ Y ]) η \eta η
由于以上两点的扩展,广义线性模型的应用比基本线性模型广泛许多。对于广义线性这个术语,可以理解为广义体现在因变量的分布形式比较广,只要是一指数分布族即可,而线性则体现在自然参数η = θ T x \eta ={{\theta }^{T}}x η = θ T x θ \theta θ
这一家族中的模型形式基本上都差不多,不同的就是因变量(Y)不同,如果是连续的,就是多重线性回归,如果是伯努利分布,就是 logistic 回归,如果是 poisson 分布,就是 poisson 回归,如果是负二项分布,就是负二项回归,等等。只要注意区分它们的因变量就可以了。logistic 回归的因变量可以是二分类的(二项逻辑回归),也可以是多分类的(多项逻辑回归或者 softmax 回归),但是二分类的更为常用,也更加容易解释。所以实际中最为常用的就是二分类的 logistic 回归。
根据sklearn 中的广义线性回归 Generalized Linear Regression 的第二种方式exponential dispersion model (EDM) :
其实就是要让真实 y 与预测 y 之间的差异越小越好:min w 1 2 n samples ∑ i d ( y i , y ^ i ) + α 2 ∥ w ∥ 2 \min_{w} \frac{1}{2 n_{\text{samples}}} \sum_i d(y_i, \hat{y}_i) + \frac{\alpha}{2} \|w\|_2 w min 2 n samples 1 i ∑ d ( y i , y ^ i ) + 2 α ∥ w ∥ 2
假设 y 分别符合下列分布,求真实 y 与预测 y 之间的差异(Deviance)(log 相减不就是两个概率之间的比吗?不就是对数几率(log odds)吗?对数几率为 0 时不就是概率比为 1 吗?不就是差异最小么!):
Normal(Gaussian) :f ( y ; μ , σ ) = 1 2 π σ 2 exp ( − ( y − μ ) 2 2 σ 2 ) f(y;\mu,\sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{(y-\mu)^2}{2\sigma^2}) f ( y ; μ , σ ) = 2 π σ 2 1 exp ( − 2 σ 2 ( y − μ ) 2 ) log f ( y ; μ , σ ) = − log 2 π σ 2 − y 2 − 2 y μ + μ 2 2 σ 2 = − log 2 π σ 2 − y 2 2 σ 2 − − 2 y μ + μ 2 2 σ 2 \log f(y;\mu,\sigma) = -\log\sqrt{2\pi\sigma^2} - \frac{y^2-2y\mu+\mu^2}{2\sigma^2}= -\log\sqrt{2\pi\sigma^2} - \frac{y^2}{2\sigma^2} - \frac{-2y\mu+\mu^2}{2\sigma^2} log f ( y ; μ , σ ) = − log 2 π σ 2 − 2 σ 2 y 2 − 2 y μ + μ 2 = − log 2 π σ 2 − 2 σ 2 y 2 − 2 σ 2 − 2 y μ + μ 2 y ^ \hat{y} y ^ μ \mu μ log f ( y ; y , σ ) − log f ( y ; y ^ , σ ) = − − 2 y . y + y 2 2 σ 2 − ( − − 2 y . y ^ + y ^ 2 2 σ 2 ) = y 2 − 2 y . y ^ + y ^ 2 2 σ 2 = ( y − y ^ ) 2 2 σ 2 = D ( y , y ^ ) 2 σ 2 \log f(y;y,\sigma) - \log f(y;\hat{y},\sigma) = - \frac{-2y.y+y^2}{2\sigma^2} - (- \frac{-2y.\hat{y}+\hat{y}^2}{2\sigma^2}) \\= \frac{y^2 -2y.\hat{y}+\hat{y}^2}{2\sigma^2} \\= \frac{(y-\hat{y})^2}{2\sigma^2} \\= \frac{D(y,\hat{y})}{2\sigma^2} log f ( y ; y , σ ) − log f ( y ; y ^ , σ ) = − 2 σ 2 − 2 y . y + y 2 − ( − 2 σ 2 − 2 y . y ^ + y ^ 2 ) = 2 σ 2 y 2 − 2 y . y ^ + y ^ 2 = 2 σ 2 ( y − y ^ ) 2 = 2 σ 2 D ( y , y ^ )
Poisson :f ( y ; μ ) = μ y e − μ y ! f(y;\mu) = \frac{\mu^y e^{-\mu}}{y!} f ( y ; μ ) = y ! μ y e − μ log f ( y ; μ ) = y log μ − μ − log ( y ! ) \log f(y;\mu) = y\log\mu -\mu -\log(y!) log f ( y ; μ ) = y log μ − μ − log ( y !) y ^ \hat{y} y ^ μ \mu μ log f ( y ; y ) − log f ( y ; y ^ ) = y log y y ^ − y + y ^ \log f(y;y) -\log f(y;\hat{y}) = y\log\frac{y}{\hat{y}} - y + \hat{y} log f ( y ; y ) − log f ( y ; y ^ ) = y log y ^ y − y + y ^
Binomial(sklearn 中没有) :f ( y ; n , p ) = ( n y ) p y ( 1 − p ) n − y f(y;n,p) = \binom{n}{y} p^y (1-p)^{n-y} f ( y ; n , p ) = ( y n ) p y ( 1 − p ) n − y log f ( y ; n , p ) = y log p + ( n − y ) log ( 1 − p ) + log ( ( n y ) ) \log f(y;n,p) =y\log p+(n-y)\log(1-p) + \log(\binom{n}{y}) log f ( y ; n , p ) = y log p + ( n − y ) log ( 1 − p ) + log ( ( y n ) ) y ^ \hat{y} y ^ y ^ = μ = n p \hat{y} = \mu = np y ^ = μ = n p log f ( y ; n , y n ) − log f ( y ; n , y ^ n ) = y log y y ^ + ( n − y ) log 1 − y n 1 − y ^ n = y log y y ^ + ( n − y ) log n − y n − y ^ \log f(y;n,\frac{y}{n}) - \log f(y;n,\frac{\hat{y}}{n})= y\log\frac{y}{\hat{y}} + (n-y)\log\frac{1-\frac{y}{n}}{1-\frac{\hat{y}}{n}} = y\log\frac{y}{\hat{y}} + (n-y)\log\frac{n-y}{n-\hat{y}} log f ( y ; n , n y ) − log f ( y ; n , n y ^ ) = y log y ^ y + ( n − y ) log 1 − n y ^ 1 − n y = y log y ^ y + ( n − y ) log n − y ^ n − y
上述计算都有一个 2 倍,不知道什么意思所以没有写出来。广义线性模型(GLM) 。
Logistic 函数 (Logistic function )的公式定义:
f ( x ) = L 1 + e − k ( x − x 0 ) {\displaystyle f(x)={\frac {L}{1+e^{-k(x-x_{0})}}}} f ( x ) = 1 + e − k ( x − x 0 ) L L L L x 0 x_0 x 0 K K K
逻辑斯谛分布 Logistic distribution :
分布函数 CDF(Cumulative distribution function):F ( x ; μ , s ) = 1 1 + e − ( x − μ ) / s = 1 2 + 1 2 tanh ( x − μ 2 s ) . {\displaystyle F(x;\mu ,s)={\frac {1}{1+e^{-(x-\mu )/s}}}={\frac {1}{2}}+{\frac {1}{2}}\operatorname {tanh} \left({\frac {x-\mu }{2s}}\right).} F ( x ; μ , s ) = 1 + e − ( x − μ ) / s 1 = 2 1 + 2 1 tanh ( 2 s x − μ ) .
密度函数 PDF(Probability density function):f ( x ; μ , s ) = e − ( x − μ ) / s s ( 1 + e − ( x − μ ) / s ) 2 = 1 s ( e ( x − μ ) / ( 2 s ) + e − ( x − μ ) / ( 2 s ) ) 2 = 1 4 s sech 2 ( x − μ 2 s ) . {\displaystyle {\begin{aligned}f(x;\mu ,s)&={\frac {e^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}\\[4pt]&={\frac {1}{s\left(e^{(x-\mu )/(2s)}+e^{-(x-\mu )/(2s)}\right)^{2}}}\\[4pt]&={\frac {1}{4s}}\operatorname {sech} ^{2}\left({\frac {x-\mu }{2s}}\right).\end{aligned}}} f ( x ; μ , s ) = s ( 1 + e − ( x − μ ) / s ) 2 e − ( x − μ ) / s = s ( e ( x − μ ) / ( 2 s ) + e − ( x − μ ) / ( 2 s ) ) 2 1 = 4 s 1 sech 2 ( 2 s x − μ ) .
μ \mu μ standard deviation )成比例的参数
Sigmoid 函数 (Sigmoid function )的公式定义:S ( x ) = 1 1 + e − x = e x e x + 1 = 1 − S ( − x ) . {\displaystyle S(x)={\frac {1}{1+e^{-x}}}={\frac {e^{x}}{e^{x}+1}}=1-S(-x).} S ( x ) = 1 + e − x 1 = e x + 1 e x = 1 − S ( − x ) .
Sigmoid 函数是一个有界、可微的实函数,可以将输入压缩到(0,1)区间,经常用作激活函数和概率输出。σ ( x ) \sigma(x) σ ( x ) K = 1 , x 0 = 0 , L = 1 K=1,x_0=0,L=1 K = 1 , x 0 = 0 , L = 1
导数:S ′ ( x ) = S ( x ) ( 1 − S ( x ) ) S'(x)= S(x)(1-S(x)) S ′ ( x ) = S ( x ) ( 1 − S ( x )) S ( x ) = 1 1 + e − x = ( 1 + e − x ) − 1 S ′ ( x ) = ( − 1 ) ∗ ( 1 + e − x ) − 2 ∗ e − x ∗ ( − 1 ) = ( 1 + e − x ) − 2 ∗ e − x = e − x ( 1 + e − x ) 2 = 1 + e − x − 1 ( 1 + e − x ) 2 = 1 + e − x ( 1 + e − x ) 2 − 1 ( 1 + e − x ) 2 = 1 1 + e − x − 1 ( 1 + e − x ) 2 = 1 1 + e − x ( 1 − 1 1 + e − x ) S(x) = {\frac {1}{1+e^{-x}}} = (1+e^{-x})^{-1} \\ S'(x)=(-1)*(1+e^{-x})^{-2}*e^{-x}*(-1) \\= (1+e^{-x})^{-2}*e^{-x} \\= \frac{e^{-x}}{(1+e^{-x})^{2}} \\= \frac{1+e^{-x}-1}{(1+e^{-x})^{2}} \\= \frac{1+e^{-x}}{(1+e^{-x})^{2}} - \frac{1}{(1+e^{-x})^{2}} \\=\frac{1}{1+e^{-x}} - \frac{1}{(1+e^{-x})^{2}} \\= \frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}}) S ( x ) = 1 + e − x 1 = ( 1 + e − x ) − 1 S ′ ( x ) = ( − 1 ) ∗ ( 1 + e − x ) − 2 ∗ e − x ∗ ( − 1 ) = ( 1 + e − x ) − 2 ∗ e − x = ( 1 + e − x ) 2 e − x = ( 1 + e − x ) 2 1 + e − x − 1 = ( 1 + e − x ) 2 1 + e − x − ( 1 + e − x ) 2 1 = 1 + e − x 1 − ( 1 + e − x ) 2 1 = 1 + e − x 1 ( 1 − 1 + e − x 1 )
与双曲正切函数 ( hyperbolic tangent function ):f ( x ) = 1 2 + 1 2 tanh ( x 2 ) , tanh ( x ) = 2 f ( 2 x ) − 1. {\displaystyle f(x)={\frac {1}{2}}+{\frac {1}{2}}\tanh \left({\frac {x}{2}}\right),} \\ {\displaystyle \tanh(x)=2f(2x)-1.} f ( x ) = 2 1 + 2 1 tanh ( 2 x ) , tanh ( x ) = 2 f ( 2 x ) − 1.
tanh ( x ) = e x − e − x e x + e − x = e x ⋅ ( 1 − e − 2 x ) e x ⋅ ( 1 + e − 2 x ) = f ( 2 x ) − e − 2 x 1 + e − 2 x = f ( 2 x ) − e − 2 x + 1 − 1 1 + e − 2 x = 2 f ( 2 x ) − 1. {\displaystyle {\begin{aligned}\tanh(x)&={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{x}\cdot \left(1-e^{-2x}\right)}{e^{x}\cdot \left(1+e^{-2x}\right)}}\\&=f(2x)-{\frac {e^{-2x}}{1+e^{-2x}}}=f(2x)-{\frac {e^{-2x}+1-1}{1+e^{-2x}}}=2f(2x)-1.\end{aligned}}} tanh ( x ) = e x + e − x e x − e − x = e x ⋅ ( 1 + e − 2 x ) e x ⋅ ( 1 − e − 2 x ) = f ( 2 x ) − 1 + e − 2 x e − 2 x = f ( 2 x ) − 1 + e − 2 x e − 2 x + 1 − 1 = 2 f ( 2 x ) − 1.
Softmax 函数 (Softmax function ,也称为归一化指数函数 normalized exponential function)的公式定义:σ : R K → [ 0 , 1 ] K {\displaystyle \sigma :\mathbb {R} ^{K}\to [0,1]^{K}} σ : R K → [ 0 , 1 ] K
σ ( z ) i = e z i ∑ j = 1 K e z j for i = 1 , … , K and z = ( z 1 , … , z K ) ∈ R K . {\displaystyle \sigma (\mathbf {z} )_{i}={\frac {e^{z_{i}}}{\sum _{j=1}^{K}e^{z_{j}}}}\ \ \ \ {\text{ for }}i=1,\dotsc ,K{\text{ and }}\mathbf {z} =(z_{1},\dotsc ,z_{K})\in \mathbb {R} ^{K}.} σ ( z ) i = ∑ j = 1 K e z j e z i for i = 1 , … , K and z = ( z 1 , … , z K ) ∈ R K .
一般形式:σ ( z ) i = e β z i ∑ j = 1 K e β z j or σ ( z ) i = e − β z i ∑ j = 1 K e − β z j for i = 1 , … , K . {\displaystyle \sigma (\mathbf {z} )_{i}={\frac {e^{\beta z_{i}}}{\sum _{j=1}^{K}e^{\beta z_{j}}}}{\text{ or }}\sigma (\mathbf {z} )_{i}={\frac {e^{-\beta z_{i}}}{\sum _{j=1}^{K}e^{-\beta z_{j}}}}{\text{ for }}i=1,\dotsc ,K.} σ ( z ) i = ∑ j = 1 K e β z j e β z i or σ ( z ) i = ∑ j = 1 K e − β z j e − β z i for i = 1 , … , K .
性质:σ ( z + c ) j = e z j + c ∑ k = 1 K e z k + c = e z j ⋅ e c ∑ k = 1 K e z k ⋅ e c = σ ( z ) j . {\displaystyle \sigma (\mathbf {z} +\mathbf {c} )_{j}={\frac {e^{z_{j}+c}}{\sum _{k=1}^{K}e^{z_{k}+c}}}={\frac {e^{z_{j}}\cdot e^{c}}{\sum _{k=1}^{K}e^{z_{k}}\cdot e^{c}}}=\sigma (\mathbf {z} )_{j}.} σ ( z + c ) j = ∑ k = 1 K e z k + c e z j + c = ∑ k = 1 K e z k ⋅ e c e z j ⋅ e c = σ ( z ) j .
等式左边的c = ( c , … , c ) {\displaystyle \mathbf {c} =(c,\dots ,c)} c = ( c , … , c )
如果z i z_i z i ( 1 K , . . . , 1 K ) ∈ R K (\frac{1}{K},...,\frac{1}{K}) \in \mathbb{R}^K ( K 1 , ... , K 1 ) ∈ R K e C e^C e C ∑ k = 1 K e C \sum _{k=1}^{K}e^C ∑ k = 1 K e C z \mathbf {z} z max i z i \max_i {z_i} max i z i σ ( z ) i = e z i ∑ j = 1 K e z j = e ( z i − z m a x ) ∑ j = 1 K e ( z j − z m a x ) = e ( z i − z m a x ) 1 + ∑ j = 1 , j ≠ m a x K e ( z j − z m a x ) \sigma (\mathbf {z} )_{i}={\frac {e^{z_{i}}}{\sum _{j=1}^{K}e^{z_{j}}}} = {\frac {e^{(z_{i}-z_{max})}}{\sum _{j=1}^{K}e^{(z_{j}-z_{max})}}} = {\frac {e^{(z_{i}-z_{max})}}{1+\sum _{j=1,j\neq max}^{K}e^{(z_{j}-z_{max})}}} σ ( z ) i = ∑ j = 1 K e z j e z i = ∑ j = 1 K e ( z j − z ma x ) e ( z i − z ma x ) = 1 + ∑ j = 1 , j = ma x K e ( z j − z ma x ) e ( z i − z ma x )
log softmax 函数在深度学习中也经常遇见,其实就是求完 softmax,再对其求 log,如果直接计算可能会出现问题(当 softmax 很小时,log 会得到− ∞ -\infty − ∞ log ( σ ( z ) ) i = log e ( z i − z m a x ) ∑ j = 1 K e ( z j − z m a x ) = log e ( z i − z m a x ) − log ∑ j = 1 K e ( z j − z m a x ) = ( z i − z m a x ) − log ∑ j = 1 K e ( z j − z m a x ) \log(\sigma (\mathbf {z} ))_{i}=\log{\frac {e^{(z_{i}-z_{max})}}{\sum _{j=1}^{K}e^{(z_{j}-z_{max})}}} \\= \log e^{(z_{i}-z_{max})} - \log {\sum _{j=1}^{K}e^{(z_{j}-z_{max})}} \\= (z_{i}-z_{max})- \log {\sum _{j=1}^{K}e^{(z_{j}-z_{max})}} log ( σ ( z ) ) i = log ∑ j = 1 K e ( z j − z ma x ) e ( z i − z ma x ) = log e ( z i − z ma x ) − log j = 1 ∑ K e ( z j − z ma x ) = ( z i − z ma x ) − log j = 1 ∑ K e ( z j − z ma x )
而∑ j = 1 K e ( z j − z m a x ) {\sum _{j=1}^{K}e^{(z_{j}-z_{max})}} ∑ j = 1 K e ( z j − z ma x )
negative log-likelihood (NLL),likelihood 是一个概率(softmax 也是概率),所以 log-likelihood 小于 0,negative log-likelihood 则大于 0,这样就可以最小化 negative log-likelihood 了
[6-1] Berger A,Della Pietra SD,Pietra VD. A maximum entropy approach to naturallanguage processing. Computational Linguistics,1996,22(1),39–71
[6-2] Berger A. The Improved Iterative Scaling Algorithm: A Gentle Introduction.http://www.cs.cmu.edu/ afs/cs/user/aberger/www/ps/scaling.ps
[6-3] Hastie T,Tibshirani R,Friedman J. The Elements of Statistical Learning: DataMining,Inference,and Prediction. Springer-Verlag. 2001(中译本:统计学习基础——数据挖掘、推理与预测。范明,柴玉梅,昝红英等译。北京:电子工业出版社,2004)
[6-4] Mitchell TM. Machine Learning. McGraw-Hill Companies,Inc. 1997(中译本:机器学习。北京:机械工业出版社,2003)
[6-5] Collins M,Schapire RE,Singer Y. Logistic Regression,AdaBoost and BregmanDistances. Machine Learning Journal,2004
[6-6] Canu S,Smola AJ. Kernel method and exponential family. Neurocomputing,2005,69:714–720
支持向量机 (support vector machine,SVM )是一种二类分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;支持向量机还包括核技巧 ,这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化,可形式化为一个求解凸二次规划 (convex quadratic programming)的问题,也等价于正则化的合页损失函数 的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化算法。
支持向量机学习方法包含构建由简至繁的模型:线性可分支持向量机 (linear supportvector machine in linearly separable case)、线性支持向量机 (linear support vectormachine)及非线性支持向量机 (non-linear support vector machine)。简单模型是复杂模型的基础,也是复杂模型的特殊情况。当训练数据线性可分时,通过硬间隔最大化 (hardmargin maximization),学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机 ;当训练数据近似线性可分时,通过软间隔最大化 (soft marginmaximization),也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机 ;当训练数据线性不可分时,通过使用核技巧(kernel trick)及软间隔最大化,学习非线性支持向量机 。
当输入空间为欧氏空间或离散集合、特征空间为希尔伯特空间时,核函数(kernelfunction)表示将输入从输入空间映射到特征空间得到的特征向量之间的内积。通过使用核函数可以学习非线性支持向量机,等价于隐式地在高维的特征空间中学习线性支持向量机。这样的方法称为核技巧。核方法(kernel method)是比支持向量机更为一般的机器学习方法。
SVM 有三宝:间隔、对偶、核技巧
函数间隔:γ ^ = y ( w . x + b ) , y ∈ { − 1 , + 1 } \hat\gamma = y(w.x + b), y\in \{-1,+1\} γ ^ = y ( w . x + b ) , y ∈ { − 1 , + 1 } γ = 1 ∥ w ∥ ∣ w . x + b ∣ = γ ^ ∥ w ∥ \gamma = \frac{1}{\|w\|}|w.x + b| = \frac{\hat\gamma}{\|w\|} γ = ∥ w ∥ 1 ∣ w . x + b ∣ = ∥ w ∥ γ ^
w . x + b = 0 w.x + b=0 w . x + b = 0
最大间隔(硬间隔原始问题-凸二次规划)max w , b γ ^ ∥ w ∥ s.t. y i ( w . x i + b ) ≥ γ ^ \begin{aligned} &\max_{w,b} &\frac{\hat\gamma}{\|w\|} \\ &\text{s.t.} &y_i(w.x_i+b) \geq \hat\gamma\end{aligned} w , b max s.t. ∥ w ∥ γ ^ y i ( w . x i + b ) ≥ γ ^ γ ^ \hat\gamma γ ^ min w , b 1 2 ∥ w ∥ 2 s.t. y i ( w . x i + b ) ≥ 1 \begin{aligned} &\min_{w,b} &\frac{1}{2}\|w\|^2 \\ &\text{s.t.} &y_i(w.x_i+b) \geq 1\end{aligned} w , b min s.t. 2 1 ∥ w ∥ 2 y i ( w . x i + b ) ≥ 1 1 ∥ w ∥ \frac{1}{\|w\|} ∥ w ∥ 1 ∥ w ∥ = 0 \|w\| = 0 ∥ w ∥ = 0 arg max 1 ∥ w ∥ 与 arg min 1 2 ∥ w ∥ 2 \argmax \frac{1}{\|w\|} 与 \argmin \frac{1}{2}\|w\|^2 arg max ∥ w ∥ 1 与 arg min 2 1 ∥ w ∥ 2 存在且唯一 ,具体证明就不证了(见统计学习方法 117 页)。支持向量 ,也就是满足y i ( w . x i + b ) = 1 y_i(w.x_i +b ) =1 y i ( w . x i + b ) = 1 w . x i + b = + 1 , w . x i + b = − 1 w.x_i +b = +1,w.x_i +b = -1 w . x i + b = + 1 , w . x i + b = − 1 间隔边界 ,两个间隔边界之间的距离称为间隔 (margin),间隔大小为2 ∥ w ∥ \frac{2}{\|w\|} ∥ w ∥ 2 只有支持向量起作用 ,而其它样本点并不起作用,所以该模型叫做支持向量机。
拉格朗日函数(求最小)L ( w , b , α ) = 1 2 ∥ w ∥ 2 + ∑ i = 1 N α i ( 1 − y i ( w . x i + b ) ) L(w,b,\alpha) = \frac{1}{2}\|w\|^2 + \sum_{i=1}^N \alpha_i(1-y_i(w.x_i+b)) L ( w , b , α ) = 2 1 ∥ w ∥ 2 + i = 1 ∑ N α i ( 1 − y i ( w . x i + b )) min w , b max α L ( w , b , α ) \min_{w,b} \max_{\alpha} L(w,b,\alpha) w , b min α max L ( w , b , α )
拉格朗日对偶函数(求最大)max α g ( α ) = max α inf w , b L ( w , b , α ) \max_{\alpha} g(\alpha) = \max_{\alpha} \inf_{w,b} L(w,b,\alpha) α max g ( α ) = α max w , b inf L ( w , b , α )
带正则项的合页损失函数(软间隔原始问题-凸二次规划)min w , b ∑ i = 1 N max ( 0 , 1 − y i ( w . x i + b ) ) ⏟ hinge loss function + λ ∥ w ∥ 2 ⏟ 正则化项 \min_{w,b} \underbrace{\sum_{i=1}^N\max(0,1-y_i(w.x_i+b))}_{\text{hinge loss function}} + \underbrace{\lambda\|w\|^2}_{\text{正则化项}} w , b min hinge loss function i = 1 ∑ N max ( 0 , 1 − y i ( w . x i + b )) + 正则化项 λ ∥ w ∥ 2 软间隔 最大化的优化问题:min w , b , ξ ∑ i = 1 n ξ i + λ ∥ w ∥ 2 subject to y i ( w T x i + b ) ≥ 1 − ξ i ξ i ≥ 0 , for all i . \begin{aligned} &\min_{w,b,\xi} & \sum _{i=1}^{n}\xi _{i}+\lambda \|\mathbf {w} \|^{2} \\ &\displaystyle {\text{subject to }} & y_{i}(\mathbf {w} ^{T}\mathbf {x} _{i}+b)\geq 1-\xi _{i}\\ &&\xi _{i}\geq 0,\,{\text{for all }}i.\end{aligned} w , b , ξ min subject to i = 1 ∑ n ξ i + λ ∥ w ∥ 2 y i ( w T x i + b ) ≥ 1 − ξ i ξ i ≥ 0 , for all i . ξ i = max ( 0 , 1 − y i ( w T x i + b ) ) {\displaystyle \xi _{i}=\max \left(0,1-y_{i}(\mathbf {w} ^{T}\mathbf {x} _{i}+b)\right)} ξ i = max ( 0 , 1 − y i ( w T x i + b ) ) Relaxation 有很多,下面只是一种而已)(跟下面松弛变量定义不同,只有统计学习方法中有说到,其它地方没有找到)。y i ( w T x i + b ) ≥ 1 − ξ i y_{i}(\mathbf {w} ^{T}\mathbf {x} _{i}+b)\geq 1-\xi _{i} y i ( w T x i + b ) ≥ 1 − ξ i
拉格朗日函数(求最小)L ( w , b , ξ , α , μ ) = λ ∥ w ∥ 2 + ∑ i = 1 N ξ i + ∑ i = 1 N α i ( 1 − ξ i − y i ( w . x i + b ) ) + ∑ i = 1 N ( μ i ∗ ( − ξ i ) ) L(w,b,\xi,\alpha,\mu) = \lambda\|w\|^2 + \sum_{i=1}^N \xi_{i} + \sum_{i=1}^N \alpha_i(1-\xi_{i}-y_i(w.x_i+b)) + \sum_{i=1}^N(\mu_i*(-\xi_{i})) L ( w , b , ξ , α , μ ) = λ ∥ w ∥ 2 + i = 1 ∑ N ξ i + i = 1 ∑ N α i ( 1 − ξ i − y i ( w . x i + b )) + i = 1 ∑ N ( μ i ∗ ( − ξ i )) min w , b , ξ max α , μ L ( w , b , ξ , α , μ ) \min_{w,b,\xi} \max_{\alpha,\mu} L(w,b,\xi,\alpha,\mu) w , b , ξ min α , μ max L ( w , b , ξ , α , μ )
拉格朗日对偶函数(求最大)max α , μ g ( α , μ ) = max α , μ inf w , b , ξ L ( w , b , ξ , α , μ ) \max_{\alpha,\mu} g(\alpha,\mu) = \max_{\alpha,\mu} \inf_{w,b,\xi} L(w,b,\xi,\alpha,\mu) α , μ max g ( α , μ ) = α , μ max w , b , ξ inf L ( w , b , ξ , α , μ )
算法 :
核技巧 :x 用 ϕ ( x ) x用\phi (x) x 用 ϕ ( x ) ϕ ( x ) \phi (x) ϕ ( x )
书中还介绍了原形式的对偶形式 (区别于拉格朗日对偶),也就是等价形式(感知机中 2.3.3 节 44 页 也是等价的意思),这两个地方的等价都是经过基本推导,求出 w 参数,然后对原问题进行了替换。
最优化:建模、算法与理论/最优化计算方法 Stephen Boyd 的 Convex Optimization - 凸优化 Nonlinear Programming by Dimitri P. Bertsekas - 非线性规划
凸优化 (Convex optimization ):minimize x f ( x ) subject to g i ( x ) ≤ 0 , i = 1 , … , m h i ( x ) = 0 , i = 1 , … , p , {\displaystyle {\begin{aligned}&{\underset {\mathbf {x} }{\operatorname {minimize} }}&&f(\mathbf {x} )\\&\operatorname {subject\ to} &&g_{i}(\mathbf {x} )\leq 0,\quad i=1,\dots ,m\\&&&h_{i}(\mathbf {x} )=0,\quad i=1,\dots ,p,\end{aligned}}} x minimize subject to f ( x ) g i ( x ) ≤ 0 , i = 1 , … , m h i ( x ) = 0 , i = 1 , … , p , x ∈ R n \mathbf {x} \in \mathbb {R} ^{n} x ∈ R n 目标函数 (objective function)f : D ⊆ R n → R {\displaystyle f:{\mathcal {D}}\subseteq \mathbb {R} ^{n}\to \mathbb {R} } f : D ⊆ R n → R 不等式约束 g i : R n → R {\displaystyle g_{i}:\mathbb {R} ^{n}\to \mathbb {R} } g i : R n → R 等式约束 h i : R n → R {\displaystyle h_{i}:\mathbb {R} ^{n}\to \mathbb {R} } h i : R n → R 仿射 (affine )的
二次约束二次规划 (Quadratically constrained quadratic program ):minimize 1 2 x T P 0 x + q 0 T x subject to 1 2 x T P i x + q i T x + r i ≤ 0 for i = 1 , … , m , A x = b , {\begin{aligned}&{\text{minimize}}&&{\tfrac 12}x^{{\mathrm {T}}}P_{0}x+q_{0}^{{\mathrm {T}}}x\\&{\text{subject to}}&&{\tfrac 12}x^{{\mathrm {T}}}P_{i}x+q_{i}^{{\mathrm {T}}}x+r_{i}\leq 0\quad {\text{for }}i=1,\dots ,m,\\&&&Ax=b,\end{aligned}} minimize subject to 2 1 x T P 0 x + q 0 T x 2 1 x T P i x + q i T x + r i ≤ 0 for i = 1 , … , m , A x = b , P 0 以及 P 1 , . . , P m ∈ R n × n P_0以及P_1,..,P_m \in \mathbb{R}^{n \times n} P 0 以及 P 1 , .. , P m ∈ R n × n x ∈ R n \mathbf {x} \in \mathbb {R} ^{n} x ∈ R n P 0 以及 P 1 , . . , P m ∈ R n × n P_0以及P_1,..,P_m \in \mathbb{R}^{n \times n} P 0 以及 P 1 , .. , P m ∈ R n × n P 1 , . . , P m P_1,..,P_m P 1 , .. , P m 二次规划 (Quadratic programming ),即目标函数是二次的,不等式以及等式约束也是线性的;二次规划的前提下,如果P 0 P_0 P 0 凸二次规划 ;如果P 0 P_0 P 0 不标准的线性规划 (Linear programming ),即目标函数是线性的,不等式以及等式约束也是线性的。标准的线性规划 :即目标函数是线性的,非负约束(优化变量是非负的),等式约束也是线性的。
线性规划解法有单纯形法 等。其它规划的优化算法看这里 :内点法,单纯形法等;有线性规划自然也有动态规划 (Dynamic programming )
最小二乘不就是凸二次规划么 (∥ y − f ( x ) ∥ 2 , f ( x ) = A x + c \|y-f(x)\|^2,f(x) = Ax+c ∥ y − f ( x ) ∥ 2 , f ( x ) = A x + c minimize f ( x ) = 1 2 ∥ A x − b ∥ 2 = 1 2 ( A x − b ) T ( A x − b ) = 1 2 ( x T A T A x − x T A T b − b T A x + b t b ) = 1 2 ( x T A T A x − 2 x T A T b + b t b ) \text{minimize} f(x) =\frac{1}{2} \|Ax-b\|^2 = \frac{1}{2}(Ax-b)^T(Ax-b) \\= \frac{1}{2}(x^TA^TAx - x^TA^Tb -b^TAx + b^tb) \\= \frac{1}{2}(x^TA^TAx - 2x^TA^Tb + b^tb) minimize f ( x ) = 2 1 ∥ A x − b ∥ 2 = 2 1 ( A x − b ) T ( A x − b ) = 2 1 ( x T A T A x − x T A T b − b T A x + b t b ) = 2 1 ( x T A T A x − 2 x T A T b + b t b ) A ∈ R m × n , x ∈ R n × 1 , b ∈ R m × 1 A \in \mathbb{R}^{m \times n},x \in \mathbb{R}^{n \times 1},b \in \mathbb{R}^{m \times 1} A ∈ R m × n , x ∈ R n × 1 , b ∈ R m × 1 x T A T b 和 b T A x x^TA^Tb 和 b^TAx x T A T b 和 b T A x b t b b^tb b t b A T A A^TA A T A
L1 和 L2 回归也能转化称相应的优化问题 ,参考:L1L2 正则化和凸优化
共轭函数 (conjugate function ):f : R n → R f:\mathbb{R}^n \to \mathbb{R} f : R n → R f ∗ : R n → R f^*:\mathbb{R}^n \to \mathbb{R} f ∗ : R n → R f ∗ ( y ) = sup x ∈ d o m f ( y T x − f ( x ) ) f^*(y) = \sup_{x \in \mathrm{dom} f} (y^Tx - f(x)) f ∗ ( y ) = x ∈ dom f sup ( y T x − f ( x ))
拉格朗日乘数法 (Lagrange multiplier ):L ( x , λ , ν ) = f ( x ) + ∑ i = 1 m λ i g i ( x ) + ∑ i = 1 p ν i h i ( x ) L(x,\lambda,\nu) = f(x) +\sum _{i=1}^{m}\lambda _{i}g_{i}(x)+\sum _{ i=1}^{p}\nu _{i}h_{i}(x) L ( x , λ , ν ) = f ( x ) + i = 1 ∑ m λ i g i ( x ) + i = 1 ∑ p ν i h i ( x ) λ i , ν i \lambda _{i},\nu _{i} λ i , ν i λ , ν \lambda,\nu λ , ν Lagrange 乘子向量 或对偶变量 。
对偶函数 (Dual function ):g ( λ , ν ) = inf x L ( x , λ , ν ) g(\lambda,\nu) = \inf_{x} L(x,\lambda,\nu) g ( λ , ν ) = x inf L ( x , λ , ν ) Lagrange 对偶函数 。对偶函数g ( λ , ν ) ≤ p ⋆ g(\lambda,\nu) \leq p^{\star} g ( λ , ν ) ≤ p ⋆ p ⋆ p^{\star} p ⋆ d ⋆ d^{\star} d ⋆ d ⋆ ≤ p ⋆ d^{\star}\leq p^{\star} d ⋆ ≤ p ⋆ 弱对偶性 (Weak Duality ),p ⋆ − d ⋆ p^{\star}- d^{\star} p ⋆ − d ⋆ 最优对偶间隙 (Duality gap ),当d ⋆ = p ⋆ d^{\star}= p^{\star} d ⋆ = p ⋆ 强对偶性 (Strong Duality )。
所以当强对偶性成立时,拉格朗日函数的最小等价于对偶函数的最大值min x max λ , ν L ( x , λ , ν ) ⟺ max λ , ν g ( λ , ν ) \min_{x} \max_{\lambda,\nu}L(x,\lambda,\nu) \iff \max_{\lambda,\nu} g(\lambda,\nu) min x max λ , ν L ( x , λ , ν ) ⟺ max λ , ν g ( λ , ν ) 我们一般使用拉格朗日函数求最小化时的参数x x x λ , ν \lambda,\nu λ , ν max λ , ν L ( x , λ , ν ) \max_{\lambda,\nu}L(x,\lambda,\nu) max λ , ν L ( x , λ , ν ) 附录 C.3.2 )。
当强对偶性成立时,那么x ⋆ , λ ⋆ , ν ⋆ x^{\star},\lambda^{\star},\nu^{\star} x ⋆ , λ ⋆ , ν ⋆ KKT 条件 (Karush–Kuhn–Tucker conditions ):
∇ x L ( x ⋆ , λ ⋆ , ν ⋆ ) = 0 λ i ⋆ g i ( x ⋆ ) = 0 , i = 1 , 2 , . . . , m ( Complementary slackness ) λ i ⋆ ≥ 0 , i = 1 , 2 , . . . , m ( Dual feasibility ) g i ( x ⋆ ) ≤ 0 , i = 1 , 2 , . . . , m ( Primal feasibility ) h i ( x ⋆ ) = 0 , i = 1 , 2 , . . . , p ( Primal feasibility ) \nabla_x L(x^{\star},\lambda^{\star},\nu^{\star}) = 0 \\ \lambda_i^{\star}g_i(x^{\star}) = 0,i=1,2,...,m \quad (\text{Complementary slackness})\\ \lambda_i^{\star} \geq 0,i=1,2,...,m \quad (\text{Dual feasibility})\\ g_i(x^{\star}) \leq 0,i=1,2,...,m \quad (\text{Primal feasibility})\\ h_i(x^{\star}) = 0,i=1,2,...,p \quad (\text{Primal feasibility}) ∇ x L ( x ⋆ , λ ⋆ , ν ⋆ ) = 0 λ i ⋆ g i ( x ⋆ ) = 0 , i = 1 , 2 , ... , m ( Complementary slackness ) λ i ⋆ ≥ 0 , i = 1 , 2 , ... , m ( Dual feasibility ) g i ( x ⋆ ) ≤ 0 , i = 1 , 2 , ... , m ( Primal feasibility ) h i ( x ⋆ ) = 0 , i = 1 , 2 , ... , p ( Primal feasibility )
可以看到我们只对 x 参数求导,没有对 Lagrange 乘子求导;
其中互补松弛 (Complementary slackness)条件用∑ i = 0 m λ i ⋆ g i ( x ⋆ ) = 0 \sum_{i=0}^m\lambda_i^{\star}g_i(x^{\star})=0 ∑ i = 0 m λ i ⋆ g i ( x ⋆ ) = 0 x ⋆ x^{\star} x ⋆ g i ( x ) = 0 g_i(x) = 0 g i ( x ) = 0 λ i ⋆ > 0 \lambda_i^{\star} > 0 λ i ⋆ > 0 x ⋆ x^{\star} x ⋆ g i ( x ) < 0 g_i(x) < 0 g i ( x ) < 0 λ i ⋆ = 0 \lambda_i^{\star} = 0 λ i ⋆ = 0 互补松弛条件说明当最优解出现在不等式约束的内部,则约束失效 ,所以λ i ⋆ ≥ 0 , i = 1 , 2 , . . . , m \lambda_i^{\star} \geq 0,i=1,2,...,m λ i ⋆ ≥ 0 , i = 1 , 2 , ... , m
如何将不标准的优化问题转换称标准的优化问题(线性规划):参考线性规划问题
a T x ≤ b a^Tx \leq b a T x ≤ b Slack variable ),松弛变量是添加到不等式约束以将其转换为等式的变量,松弛变量特别用于线性规划。松弛变量不能取负值,因为单纯形算法要求它们为正值或零。a T x + s = b s ≥ 0 a^Tx +s = b \\ s \geq 0 a T x + s = b s ≥ 0
a T x ≥ b a^Tx \geq b a T x ≥ b a T x − e = b e ≥ 0 a^Tx - e = b \\ e \geq 0 a T x − e = b e ≥ 0
B. 无约束变量变成有非负约束变量:z 1 = z 1 + − z 1 − ∣ z 1 ∣ = z 1 + + z 1 − ⟨ z 1 + , z 1 − ⟩ = 0 z 1 + , z 1 − ≥ 0 {\begin{aligned}&z_{1}=z_{1}^{+}-z_{1}^{-} \\& |z_{1}| = z_{1}^{+}+\,z_{1}^{-} \\&\braket{z_{1}^{+},z_{1}^{-}} = 0 \\&z_{1}^{+},\,z_{1}^{-} \geq 0\end{aligned}} z 1 = z 1 + − z 1 − ∣ z 1 ∣ = z 1 + + z 1 − ⟨ z 1 + , z 1 − ⟩ = 0 z 1 + , z 1 − ≥ 0
如:5 = 5 − 0 − 5 = 0 − 5 5 = 5-0 \\ -5 = 0-5 5 = 5 − 0 − 5 = 0 − 5
( 1 2 − 3 − 4 ) = ( 1 2 0 0 ) − ( 0 0 3 4 ) \begin{pmatrix}
1 \\
2 \\
-3 \\
-4
\end{pmatrix} =
\begin{pmatrix}
1 \\
2 \\
0 \\
0
\end{pmatrix} -
\begin{pmatrix}
0 \\
0 \\
3 \\
4
\end{pmatrix} ⎝ ⎛ 1 2 − 3 − 4 ⎠ ⎞ = ⎝ ⎛ 1 2 0 0 ⎠ ⎞ − ⎝ ⎛ 0 0 3 4 ⎠ ⎞
b. 目标函数有带绝对值的(第二条性质)max ∣ x ∣ 等价: max x + + x − s . t . x + ≥ 0 x − ≥ 0 \begin{aligned} \max |x| \\ 等价:\max x^+ + x^- \\ s.t. \quad x^+ \geq 0 \\ x^- \geq 0\end{aligned} max ∣ x ∣ 等价: max x + + x − s . t . x + ≥ 0 x − ≥ 0
[7-1] Cortes C,Vapnik V. Support-vector networks. Machine Learning,1995,20
[7-2] Boser BE,Guyon IM,Vapnik VN. A training algorithm for optimal margin classifiers.In : Haussler D,ed. Proc of the 5th Annual ACM Workshop on COLT. Pittsburgh,PA,1992,144–152
[7-3] Drucker H,Burges CJC,Kaufman L,Smola A,Vapnik V. Support vector regressionmachines. In: Advances in Neural Information Processing Systems 9,NIPS 1996. MITPress,155–161
[7-4] Vapnik Vladimir N. The Nature of Statistical Learning Theory. Berlin: Springer-Verlag,1995(中译本:张学工,译。统计学习理论的本质。北京:清华大学出版社,2000)
[7-5] Platt JC. Fast training of support vector machines using sequential minimaloptimization. Microsoft Research
[7-6] Weston JAE,Watkins C. Support vector machines for multi-class pattern recognition. In: Proceedings of the 7th European Symposium on Articial Neural Networks. 1999
[7-7] Crammer K,Singer Y. On the algorithmic implementation of multiclass kernel-basedmachines. Journal of Machine Learning Research,2001,2(Dec): 265–292
[7-8] Tsochantaridis I,Joachims T,Hofmann T,Altun Y. Large margin methods forstructured and interdependent output variables. JMLR,2005,6: 1453–1484
[7-9] Burges JC. A tutorial on support vector machines for pattern recognition. BellLaboratories,Lucent Technologies. 1997
[7-10] Cristianini N,Shawe-Taylor J. An Introduction to Support Vector Machines andOthre KernerBased Learning Methods. Cambridge University Press,2000(中译本:李国正,等译。支持向量机导论。北京:电子工业出版社,2004)
[7-11] 邓乃扬,田英杰。数据挖掘中的新方法——支持向量机。北京:科学出版社,2004
[7-12] 邓乃扬,田英杰。支持向量机——理论,算法与拓展。北京:科学出版社,2009
[7-13] Scholkpf B,Smola AJ. Learning with Kernels: Support VectorMachines,Regularization,Optimization,and Beyond. MIT Press,2002
[7-14] Herbrich R. Learning Kernel Classifiers,Theory and Algorithms. The MITPress,2002
[7-15] Hofmann T,Scholkopf B,Smola AJ. Kernel methods in machine learning. The Annalsof Statistics,2008,36(3): 1171–1220
集成学习 (Ensemble Learning )也叫集成方法(Ensemble methods)是一种将多种学习算法组合在一起以取得更好表现的一种方法。
利用成员模型的多样性来纠正某些成员模型错误的能力,常用的多样性技术 有:
最流行的方法是使用不同的数据集来训练每一个分类器,这些数据集通过从总体数据集中有放回的随机采样获得,例如 bootstrapping 或 bagging 技术
在分类的场景中,可使用弱分类器 或者不稳定模型(unstable model)作为成员模型来提高多样性,因为即使对训练参数进行微调,也会得到完全不同的决策边界;
也可以使用不同类型的分类器,如决策树,最近邻,支持向量机等混合到一起来增加多样性;
弱分类器:比随机猜测略好,如二分类中,准确率大于 0.5 就可以了(如 0.51)。
参见的集成学习类型:
Bayes optimal classifier
Bootstrap aggregating (也称为 bagging 来自 b ootstrap agg regating )Boosting Bayesian model averaging
Bayesian model combination
Bucket of models
Stacking
模型的组合(blending)方法:
线性组合(平均法-加权平均法) - 用于回归和分类问题f ‾ ( y ∣ x ) = ∑ t = 1 T w t f t ( y ∣ x ) \overline{f}(y|x) = \sum_{t=1}^T w_t f_t(y|x) f ( y ∣ x ) = t = 1 ∑ T w t f t ( y ∣ x ) w t = 1 T w_t = \frac{1}{T} w t = T 1
投票组合 - 用于分类问题H ( x ) = s i g n ( ∑ t = 1 T w t h t ( y ∣ x ) ) H(\textbf{x}) = sign( \sum_{t=1}^{T}w_t h_t(y|\textbf{x} ) ) H ( x ) = s i g n ( t = 1 ∑ T w t h t ( y ∣ x )) h t ( y ∣ x ) ∈ { − 1 , + 1 } h_t(y|\textbf{x} ) \in \{-1,+1\} h t ( y ∣ x ) ∈ { − 1 , + 1 }
乘积组合f ‾ ( y ∣ x ) = 1 Z ∏ t = 1 T f t ( y ∣ x ) w t \overline f(y|\textbf{x}) = \frac{1}{Z}\prod_{t=1}^{T} f_t(y | \textbf{x})^{w_t} f ( y ∣ x ) = Z 1 t = 1 ∏ T f t ( y ∣ x ) w t
学习组合初级学习器 ,再把初级学习器的输出 组合成新的数据集,用于训练次级学习器 。对于测试集,我们首先用初级学习器预测一次,得到次级学习器的输入样本,再用次级学习器预测一次,得到最终的预测结果。
aggregation type
blending
learning
uniform
voting/averaging
Bagging
non-uniform
linear
AdaBoost
conditional
stacking
Decision Tree
参考
AdaBoost :AdaBoost 是 Adaptive Boosting 的缩写
训练集T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } , x i ∈ R n , y i ∈ { − 1 , + 1 } T = \{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}, x_i \in \mathbb{R}^n,y_i\in \{-1,+1\} T = {( x 1 , y 1 ) , ( x 2 , y 2 ) , ... , ( x N , y N )} , x i ∈ R n , y i ∈ { − 1 , + 1 }
Gradient Tree Boosting :梯度提升(Gradient boosting )是一种用于回归、分类和其他任务的机器学习技术,它以弱预测模型(通常是决策树)的集合形式生成预测模型。当决策树是弱学习器时,产生的算法称为梯度提升树 (Gradient Tree Boosting or Gradient boosted trees or Gradient Boosted Decision Trees(GBDT)),通常优于随机森林(Random forest 它是 Bagging 算法的进化版,也就是说,它的思想仍然是 bagging,但是进行了独有的改进。)
随机森林与一般的 bagging 相比:(参考:Bagging 与随机森林算法原理小结 和机器学习算法系列(五):bagging 与随机森林对比及随机森林模型参数介绍 )
bagging 方法的的随机性仅仅来自样本扰动,随机林模型中引入了属性扰动,这样使得最终模型的泛化性能可以通过个体学习器之间的差异度的增加而进一步提升。
和 bagging 相比,随机森林的起始性能往往比较差,然而随着个体学习器数目的增加,随机森林会收敛到更小的误差。
随机森林的训练效率优于 bagging,因为 bagging 中的每棵树是对所有特征进行考察,而随机森林仅仅考虑一个特征子集(max_features:随机森林允许单个决策树使用特征的最大数量。)。
因为 Bagging 使用的有放回采样,所以 BaggingClassifier or RandomForestClassifier 都具有 oobscore 属性:约有 37%(lim n → − ∞ ( 1 − 1 / n ) n = 1 / e \lim_{n \to -\infty}(1-1/n)^n=1/e lim n → − ∞ ( 1 − 1/ n ) n = 1/ e score 时,也可以看下 oob_score 的情况
[8-1] Freund Y,Schapire RE. A short introduction to boosting . Journal of Japanese Societyfor Artificial Intelligence,1999,14(5): 771–780
[8-2] Hastie T,Tibshirani R,Friedman J. The Elements of Statistical Learning: DataMining,Inference,and Prediction . Springer-Verlag,2001(中译本:统计学习基础——数据挖掘、推理与预测。范明,柴玉梅,昝红英,等译。北京:电子工业出版社,2004)
[8-3] Valiant LG. A theory of the learnable . Communications of the ACM,1984,27(11):1134–1142
[8-4] Schapire R. The strength of weak learnability . Machine Learning,1990,5(2): 197–227
[8-5] Freund Y,Schapire RE. A decision-theoretic generalization of on-line learning and anapplication to boosting . Computational Learning Theory. Lecture Notes in ComputerScience,Vol. 904,1995,23–37 (55, 119-139 (1997) )
[8-6] Friedman J,Hastie T,Tibshirani R. Additive logistic regression: a statistical view ofboosting(with discussions) . Annals of Statistics,2000,28: 337–407
[8-7] Friedman J. Greedy function approximation: a gradient boosting machine . Annals ofStatistics,2001,29(5)
[8-8] Schapire RE,Singer Y. Improved boosting algorithms using confidence-ratedpredictions . Machine Learning,1999,37(3): 297–336
[8-9] Collins M,Schapire R E,Singer Y. Logistic regression,AdaBoost and Bregmandistances . Machine Learning Journal,2004
EM 算法(Expectation–maximization algorithm )是一种迭代算法,用于含有隐变量 (hidden(unseen or unmeasurable) variable or Latent variable)的概率模型参数的极大似然估计,或极大后验概率估计。EM 算法的每次迭代由两步组成:E 步,求期望(expectation);M 步,求极大(maximization)。所以这一算法称为期望极大算法(expectation maximization algorithm),简称 EM 算法。
概率模型有时既含有观测变量(observable variable),又含有隐变量或潜在变量(latent variable)。如果概率模型的变量都是观测变量,那么给定数据,可以直接用极大似然估计法,或贝叶斯估计法估计模型参数。但是,当模型含有隐变量时,就不能简单地使用这些估计方法。EM 算法就是含有隐变量的概率模型参数的极大似然估计法,或极大后验概率估计法。
本章首先叙述 EM 算法,然后讨论 EM 算法的收敛性;作为 EM 算法的应用,介绍高斯混合模型的学习;最后叙述 EM 算法的推广——GEM 算法(generalized expectation maximization (GEM) algorithm,广义 EM 算法)。
EM 算法是一个优化算法,不是一个统计学习模型。
观测数据X = { x i } i = 1 N X=\{x_i\}_{i=1}^N X = { x i } i = 1 N Z = { z i } i = 1 N Z=\{z_i\}_{i=1}^N Z = { z i } i = 1 N θ \theta θ T = { ( x 1 , z 1 ) , . . . , ( x N , z N ) } T=\{(x_1,z_1),...,(x_N,z_N)\} T = {( x 1 , z 1 ) , ... , ( x N , z N )}
注意下列公式中∣ | ∣ ; ; ; θ \theta θ θ ( 0 ) \theta^{(0)} θ ( 0 )
如果不考虑隐藏数据,我们就可以直接使用极大似然估计的方法估计出参数 θ \theta θ θ M L E = arg max θ log p ( x ∣ θ ) = arg max θ ∑ i N log p ( x i ∣ θ ) \theta_{MLE} = \arg\max\limits_\theta\log p(x|\theta) = \arg\max\limits_\theta\sum_i^N\log p(x_i|\theta) θ M L E = arg θ max log p ( x ∣ θ ) = arg θ max i ∑ N log p ( x i ∣ θ )
但由于隐藏数据的存在, 我们有 x 的边际似然函数(Marginal Likelihood ),在贝叶斯统计的上下文中,边际似然也称为证据(Evidence)p ( x ∣ θ ) = ∑ z p ( x , z ∣ θ ) = ∫ Z p ( x , z ∣ θ ) d z p(x|\theta) = \sum_{z} p(x, z|\theta) = \int_Z p(x, z|\theta)dz p ( x ∣ θ ) = z ∑ p ( x , z ∣ θ ) = ∫ Z p ( x , z ∣ θ ) d z
下面来介绍EM 算法 :
随机化参数θ ( 0 ) \theta^{(0)} θ ( 0 )
假设在第 t t t θ ( t ) \theta^{(t)} θ ( t ) t + 1 t+1 t + 1 Q ( θ , θ ( t ) ) = ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) d Z = E Z ∣ X , θ ( t ) [ log P ( X , Z ∣ θ ) ] Q(\theta,\theta^{(t)}) = \int_Z P(Z|X,\theta^{(t)}) \log P(X,Z|\theta) dZ \\ =\mathbb{E}_{Z|X,\theta^{(t)}}[\log P(X,Z|\theta)] Q ( θ , θ ( t ) ) = ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) d Z = E Z ∣ X , θ ( t ) [ log P ( X , Z ∣ θ )] 全数据的对数似然函数log p ( x , z ∣ θ ) \log p(x, z|\theta) log p ( x , z ∣ θ ) X X X θ ( t ) \theta^{(t)} θ ( t ) Z Z Z p ( z ∣ x , θ ( t ) ) p(z|x,\theta^{(t)}) p ( z ∣ x , θ ( t ) )
注意 Q 函数的第一个参数是自变量,第二个参数是已知的(上一步求得的)
b. M-step: 最大化Q ( θ , θ ( t ) ) Q(\theta,\theta^{(t)}) Q ( θ , θ ( t ) ) θ ( t + 1 ) \theta^{(t+1)} θ ( t + 1 ) θ ( t + 1 ) = arg max θ Q ( θ , θ ( t ) ) \theta^{(t+1)} = \arg\max\limits_\theta Q(\theta, \theta^{(t)}) θ ( t + 1 ) = arg θ max Q ( θ , θ ( t ) )
重复 2,直到收敛。θ ( t + 1 ) − θ ( t ) ≤ ε \theta^{(t+1)}-\theta^{(t)} \leq \varepsilon θ ( t + 1 ) − θ ( t ) ≤ ε Q ( θ ( t + 1 ) , θ ( t ) ) − Q ( θ ( t ) , θ ( t ) ) ≤ ε Q(\theta^{(t+1)},\theta^{(t)})-Q(\theta^{(t)},\theta^{(t)}) \leq \varepsilon Q ( θ ( t + 1 ) , θ ( t ) ) − Q ( θ ( t ) , θ ( t ) ) ≤ ε
EM 算法的导出 :P ( X ∣ θ ) = P ( X , Z ∣ θ ) P ( Z ∣ X , θ ) ⟹ log P ( X ∣ θ ) = log P ( X , Z ∣ θ ) − log P ( Z ∣ X , θ ) P(X|\theta) = \frac{P(X,Z|\theta)}{P(Z|X, \theta)} \implies \log P(X|\theta) = \log P(X,Z|\theta) - \log P(Z|X,\theta) P ( X ∣ θ ) = P ( Z ∣ X , θ ) P ( X , Z ∣ θ ) ⟹ log P ( X ∣ θ ) = log P ( X , Z ∣ θ ) − log P ( Z ∣ X , θ ) q ( z ) q(z) q ( z ) p ( z ∣ x ) p(z|x) p ( z ∣ x ) log P ( X ∣ θ ) = log P ( X , Z ∣ θ ) q ( Z ) − log P ( Z ∣ X , θ ) q ( Z ) \log P(X|\theta) = \log \frac{P(X,Z|\theta)}{q(Z)} - \log \frac{P(Z|X,\theta)}{q(Z)} log P ( X ∣ θ ) = log q ( Z ) P ( X , Z ∣ θ ) − log q ( Z ) P ( Z ∣ X , θ ) Z Z Z E Z [ log P ( X ∣ θ ) ] = E _ Z [ log P ( X , Z ∣ θ ) q ( Z ) ] − E _ Z [ log P ( Z ∣ X , θ ) q ( Z ) ] \mathbb{E}_Z[\log P(X|\theta)] = \mathbb{E}\_Z[\log \frac{P(X,Z|\theta)}{q(Z)}] - \mathbb{E}\_Z[\log \frac{P(Z|X,\theta)}{q(Z)}] E Z [ log P ( X ∣ θ )] = E _ Z [ log q ( Z ) P ( X , Z ∣ θ ) ] − E _ Z [ log q ( Z ) P ( Z ∣ X , θ ) ] ∫ Z q ( Z ) log P ( X ∣ θ ) d Z = ∫ Z q ( Z ) log P ( X , Z ∣ θ ) q ( Z ) d Z − ∫ Z q ( Z ) log P ( Z ∣ X , θ ) q ( Z ) d Z \int_Z q(Z)\log P(X|\theta)dZ = \int_Zq(Z)\log \frac{P(X,Z|\theta)}{q(Z)}dZ - \int_Zq(Z)\log \frac{P(Z|X,\theta)}{q(Z)}dZ ∫ Z q ( Z ) log P ( X ∣ θ ) d Z = ∫ Z q ( Z ) log q ( Z ) P ( X , Z ∣ θ ) d Z − ∫ Z q ( Z ) log q ( Z ) P ( Z ∣ X , θ ) d Z Z Z Z ∫ Z q ( Z ) d Z = 1 \int_Zq(Z)dZ = 1 ∫ Z q ( Z ) d Z = 1 log P ( X ∣ θ ) = ∫ Z q ( Z ) log P ( X , Z ∣ θ ) q ( Z ) d Z − ∫ Z q ( Z ) log P ( Z ∣ X , θ ) q ( Z ) d Z = ∫ Z q ( Z ) log P ( X , Z ∣ θ ) q ( Z ) d Z + D K L ( q ( Z ) ∣ ∣ P ( Z ∣ X , θ ) ) = E L B O + D ∗ K L ( q ( Z ) ∣ ∣ P ( Z ∣ X , θ ) ) \log P(X|\theta) = \int_Zq(Z)\log \frac{P(X,Z|\theta)}{q(Z)}dZ - \int_Zq(Z)\log \frac{P(Z|X,\theta)}{q(Z)}dZ \\ = \int_Zq(Z)\log \frac{P(X,Z|\theta)}{q(Z)}dZ + D_{KL}(q(Z)||P(Z|X,\theta)) \\= ELBO + D*{KL}(q(Z)||P(Z|X,\theta)) log P ( X ∣ θ ) = ∫ Z q ( Z ) log q ( Z ) P ( X , Z ∣ θ ) d Z − ∫ Z q ( Z ) log q ( Z ) P ( Z ∣ X , θ ) d Z = ∫ Z q ( Z ) log q ( Z ) P ( X , Z ∣ θ ) d Z + D K L ( q ( Z ) ∣∣ P ( Z ∣ X , θ )) = E L BO + D ∗ K L ( q ( Z ) ∣∣ P ( Z ∣ X , θ )) D ∗ K L = 0 , 即 q ( Z ) = P ( Z ∣ X , θ ( t ) ) D*{KL} = 0, 即 q(Z)=P(Z|X,\theta^{(t)}) D ∗ K L = 0 , 即 q ( Z ) = P ( Z ∣ X , θ ( t ) ) θ ^ = arg max θ ∫ Z q ( Z ) log P ( X , Z ∣ θ ) q ( Z ) d Z = arg max θ ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) P ( Z ∣ X , θ ( t ) ) d Z \hat{\theta} = \argmax_{\theta}\int_Zq(Z)\log \frac{P(X,Z|\theta)}{q(Z)}dZ \\ = \argmax_{\theta}\int_Z P(Z|X,\theta^{(t)})\log \frac{P(X,Z|\theta)}{P(Z|X,\theta^{(t)})}dZ θ ^ = θ arg max ∫ Z q ( Z ) log q ( Z ) P ( X , Z ∣ θ ) d Z = θ arg max ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( Z ∣ X , θ ( t ) ) P ( X , Z ∣ θ ) d Z θ ( t ) \theta^{(t)} θ ( t ) θ ^ = arg max θ ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) d Z − ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( Z ∣ X , θ ( t ) ) d Z = arg max θ ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) d Z − C = arg max θ ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) d Z = arg max θ Q ( θ , θ ( t ) ) \hat{\theta} = \argmax_{\theta} \int_Z P(Z|X,\theta^{(t)})\log P(X,Z|\theta)dZ - \int_Z P(Z|X,\theta^{(t)})\log {P(Z|X,\theta^{(t)})}dZ \\ = \argmax_{\theta} \int_Z P(Z|X,\theta^{(t)})\log P(X,Z|\theta)dZ - C \\ = \argmax_{\theta} \int_Z P(Z|X,\theta^{(t)})\log P(X,Z|\theta)dZ \\= \argmax_{\theta} Q(\theta,\theta^{(t)}) θ ^ = θ arg max ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) d Z − ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( Z ∣ X , θ ( t ) ) d Z = θ arg max ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) d Z − C = θ arg max ∫ Z P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) d Z = θ arg max Q ( θ , θ ( t ) )
参考EM 算法 11.2.2.1 节 深入理解 EM 算法(ELBO+KL 形式) 深入理解 EM 算法-Jensen 不等式
EM 算法的收敛性 :p ( X ∣ θ ) p(\mathbf {X} \mid {\boldsymbol {\theta }}) p ( X ∣ θ ) log p ( X ∣ θ ) \log p(\mathbf {X} \mid {\boldsymbol {\theta }}) log p ( X ∣ θ ) log p ( X ∣ θ ( t + 1 ) ) ≥ log p ( X ∣ θ ( t ) ) \log p(\mathbf {X} \mid {\boldsymbol {\theta^{(t+1)} }}) \geq \log p(\mathbf {X} \mid {\boldsymbol {\theta^{(t)} }}) log p ( X ∣ θ ( t + 1 ) ) ≥ log p ( X ∣ θ ( t ) )
方法一:根据维基百科log p ( X ∣ θ ) = log p ( X , Z ∣ θ ) − log p ( Z ∣ X , θ ) . {\displaystyle \log p(\mathbf {X} \mid {\boldsymbol {\theta }})=\log p(\mathbf {X} ,\mathbf {Z} \mid {\boldsymbol {\theta }})-\log p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}).} log p ( X ∣ θ ) = log p ( X , Z ∣ θ ) − log p ( Z ∣ X , θ ) . log p ( X ∣ θ ) = ∑ Z p ( Z ∣ X , θ ( t ) ) log p ( X , Z ∣ θ ) − ∑ Z p ( Z ∣ X , θ ( t ) ) log p ( Z ∣ X , θ ) = Q ( θ ∣ θ ( t ) ) + H ( θ ∣ θ ( t ) ) , {\displaystyle {\begin{aligned}\log p(\mathbf {X} \mid {\boldsymbol {\theta }})&=\sum _{\mathbf {Z} }p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)})\log p(\mathbf {X} ,\mathbf {Z} \mid {\boldsymbol {\theta }})-\sum _{\mathbf {Z} }p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)})\log p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }})\\&=Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})+H({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)}),\end{aligned}}} log p ( X ∣ θ ) = Z ∑ p ( Z ∣ X , θ ( t ) ) log p ( X , Z ∣ θ ) − Z ∑ p ( Z ∣ X , θ ( t ) ) log p ( Z ∣ X , θ ) = Q ( θ ∣ θ ( t ) ) + H ( θ ∣ θ ( t ) ) , log p ( X ∣ θ ) − log p ( X ∣ θ ( t ) ) = Q ( θ ∣ θ ( t ) ) − Q ( θ ( t ) ∣ θ ( t ) ) + H ( θ ∣ θ ( t ) ) − H ( θ ( t ) ∣ θ ( t ) ) , {\displaystyle \log p(\mathbf {X} \mid {\boldsymbol {\theta }})-\log p(\mathbf {X} \mid {\boldsymbol {\theta }}^{(t)}) =Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})-Q({\boldsymbol {\theta }}^{(t)}\mid {\boldsymbol {\theta }}^{(t)})+H({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})-H({\boldsymbol {\theta } }^{(t)}\mid {\boldsymbol {\theta }}^{(t)}),} log p ( X ∣ θ ) − log p ( X ∣ θ ( t ) ) = Q ( θ ∣ θ ( t ) ) − Q ( θ ( t ) ∣ θ ( t ) ) + H ( θ ∣ θ ( t ) ) − H ( θ ( t ) ∣ θ ( t ) ) , 吉布斯不等式(Gibbs' inequality) H ( θ ∣ θ ( t ) ) ≥ H ( θ ( t ) ∣ θ ( t ) ) {\displaystyle H({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})\geq H({\boldsymbol {\theta }}^{(t)}\mid {\boldsymbol {\theta }}^{(t)})} H ( θ ∣ θ ( t ) ) ≥ H ( θ ( t ) ∣ θ ( t ) ) log p ( X ∣ θ ) − log p ( X ∣ θ ( t ) ) ≥ Q ( θ ∣ θ ( t ) ) − Q ( θ ( t ) ∣ θ ( t ) ) . {\displaystyle \log p(\mathbf {X} \mid {\boldsymbol {\theta }})-\log p(\mathbf {X} \mid {\boldsymbol {\theta }}^{(t)})\geq Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})-Q({\boldsymbol {\theta }}^{(t)}\mid {\boldsymbol {\theta }}^{(t)}).} log p ( X ∣ θ ) − log p ( X ∣ θ ( t ) ) ≥ Q ( θ ∣ θ ( t ) ) − Q ( θ ( t ) ∣ θ ( t ) ) . Q ( θ , θ ( t ) ) Q(\theta,\theta^{(t)}) Q ( θ , θ ( t ) ) Q ( θ ∣ θ ( t ) ) ≥ Q ( θ ( t ) ∣ θ ( t ) ) Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)}) \geq Q({\boldsymbol {\theta }}^{(t)}\mid {\boldsymbol {\theta }}^{(t)}) Q ( θ ∣ θ ( t ) ) ≥ Q ( θ ( t ) ∣ θ ( t ) ) log p ( X ∣ θ ) \log p(\mathbf {X} \mid {\boldsymbol {\theta }}) log p ( X ∣ θ )
方法二:根据统计学习方法Jensen 不等式 H ( θ ∣ θ ( t ) ) − H ( θ ( t ) ∣ θ ( t ) ) = − ∑ Z p ( Z ∣ X , θ ( t ) ) log p ( Z ∣ X , θ ) + ∑ Z p ( Z ∣ X , θ ( t ) ) log p ( Z ∣ X , θ ( t ) ) = − ∑ Z p ( Z ∣ X , θ ( t ) ) log p ( Z ∣ X , θ ) p ( Z ∣ X , θ ( t ) ) ≥ − log ( ∑ Z p ( Z ∣ X , θ ) p ( Z ∣ X , θ ( t ) ) p ( Z ∣ X , θ ( t ) ) ) = − log ( ∑ Z p ( Z ∣ X , θ ) ) = − log ( 1 ) = 0 H({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)}) -H({\boldsymbol {\theta } }^{(t)}\mid {\boldsymbol {\theta }}^{(t)}) = -\sum _{\mathbf {Z} }p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)})\log p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}) + \sum _{\mathbf {Z} }p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)})\log p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }^{(t)}}) \\ = -\sum _{\mathbf {Z} }p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)})\log \frac{p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }})}{p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }^{(t)}})} \\ \geq -\log \bigg( \sum _{\mathbf {Z} } \frac{p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }})}{p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }^{(t)}})} p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)}) \bigg) \\= -\log \bigg( \sum _{\mathbf {Z} } p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}) \bigg) = -\log(1) = 0 H ( θ ∣ θ ( t ) ) − H ( θ ( t ) ∣ θ ( t ) ) = − Z ∑ p ( Z ∣ X , θ ( t ) ) log p ( Z ∣ X , θ ) + Z ∑ p ( Z ∣ X , θ ( t ) ) log p ( Z ∣ X , θ ( t ) ) = − Z ∑ p ( Z ∣ X , θ ( t ) ) log p ( Z ∣ X , θ ( t ) ) p ( Z ∣ X , θ ) ≥ − log ( Z ∑ p ( Z ∣ X , θ ( t ) ) p ( Z ∣ X , θ ) p ( Z ∣ X , θ ( t ) ) ) = − log ( Z ∑ p ( Z ∣ X , θ ) ) = − log ( 1 ) = 0 ∑ Z p ( Z ∣ X , θ ( t ) ) = 1 \sum _{\mathbf {Z} } p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }^{(t)}}) = 1 ∑ Z p ( Z ∣ X , θ ( t ) ) = 1
方法三:根据 KL divergence 的定义 ,并且大于等于 0H ( θ ∣ θ ( t ) ) − H ( θ ( t ) ∣ θ ( t ) ) = − ∑ Z p ( Z ∣ X , θ ( t ) ) log p ( Z ∣ X , θ ) p ( Z ∣ X , θ ( t ) ) = D K L ( p ( Z ∣ X , θ ( t ) ) ∣ ∣ p ( Z ∣ X , θ ) ) ≥ 0 H({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)}) -H({\boldsymbol {\theta } }^{(t)}\mid {\boldsymbol {\theta }}^{(t)}) = -\sum _{\mathbf {Z} }p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)})\log \frac{p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }})}{p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }^{(t)}})} \\ = D_{KL}(p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)}) || p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }})) \geq 0 H ( θ ∣ θ ( t ) ) − H ( θ ( t ) ∣ θ ( t ) ) = − Z ∑ p ( Z ∣ X , θ ( t ) ) log p ( Z ∣ X , θ ( t ) ) p ( Z ∣ X , θ ) = D K L ( p ( Z ∣ X , θ ( t ) ) ∣∣ p ( Z ∣ X , θ )) ≥ 0
参考深入理解 EM 算法-收敛性证明
广义 EM (generalized expectation maximization (GEM) algorithm)log P ( X ∣ θ ) = ∫ Z q ( Z ) log P ( X , Z ∣ θ ) q ( Z ) d Z + D K L ( q ( Z ) ∣ ∣ P ( Z ∣ X , θ ) ) \log P(X|\theta) = \int_Zq(Z)\log \frac{P(X,Z|\theta)}{q(Z)}dZ + D_{KL}(q(Z)||P(Z|X,\theta)) log P ( X ∣ θ ) = ∫ Z q ( Z ) log q ( Z ) P ( X , Z ∣ θ ) d Z + D K L ( q ( Z ) ∣∣ P ( Z ∣ X , θ )) L ( q , θ ) = ∫ Z q ( Z ) log P ( X , Z ∣ θ ) q ( Z ) d Z \mathcal{L}(q, \theta) = \int_Zq(Z)\log \frac{P(X,Z|\theta)}{q(Z)}dZ L ( q , θ ) = ∫ Z q ( Z ) log q ( Z ) P ( X , Z ∣ θ ) d Z D K L = 0 D_{KL} = 0 D K L = 0 L ( q , θ ) \mathcal{L}(q,\theta) L ( q , θ ) log P ( X ∣ θ ) \log P(X|\theta) log P ( X ∣ θ ) q ( Z ) = P ( Z ∣ X , θ ) q(Z) = P(Z|X,\theta) q ( Z ) = P ( Z ∣ X , θ ) q ( Z ) q(Z) q ( Z ) θ \theta θ D K L D_{KL} D K L q = arg min q D K L ( q ( Z ) ∣ ∣ P ( Z ∣ X , θ ) ) = arg max q L ( q , θ ) q = \arg\min\limits_q D_{KL}(q(Z)||P(Z|X,\theta))= \arg\max\limits_q \mathcal{L}(q, \theta) q = arg q min D K L ( q ( Z ) ∣∣ P ( Z ∣ X , θ )) = arg q max L ( q , θ )
E-step:固定θ = θ ( t ) \theta = \theta^{(t)} θ = θ ( t ) q ( t ) = arg max q L ( q , θ ( t ) ) q^{(t)} = \arg\max\limits_q \mathcal{L}(q, \theta^{(t)}) q ( t ) = arg q max L ( q , θ ( t ) )
M-step:固定q = q ( t ) q = q^{(t)} q = q ( t ) θ ( t + 1 ) = arg max θ L ( q ( t ) , θ ) \theta^{(t+1)} = \arg\max\limits_\theta \mathcal{L}(q^{(t)}, \theta) θ ( t + 1 ) = arg θ max L ( q ( t ) , θ )
参考深入理解 EM 算法-广义 EM
高斯混合模型 (Gaussian mixture model ):
有样本(观测数据)D a t a = { x 1 , . . . , x N } Data = \{x_1,...,x_N\} D a t a = { x 1 , ... , x N } T = { ( x 1 , z 1 ) , . . . , ( x N , z N ) } T = \{(x_1,z_1),...,(x_N,z_N)\} T = {( x 1 , z 1 ) , ... , ( x N , z N )} x i x_i x i arg max k ∈ { 1 , … , K } P ( Z i = k ∣ x i ; Θ ^ ) \text{arg max}_{k \in \{1, \dots, K \}} P(Z_i = k \mid \boldsymbol{x}_i ; \hat{\Theta}) arg max k ∈ { 1 , … , K } P ( Z i = k ∣ x i ; Θ ^ ) Θ ^ \hat{\Theta} Θ ^ P ( Z i = k ∣ x i ; Θ ^ ) = p ( x i ∣ Z i = k ; Θ ^ ) P ( Z i = k ; Θ ^ ) ∑ h = 1 K p ( x i ∣ Z i = h ; Θ ^ ) P ( Z i = h ; Θ ^ ) = ϕ ( x i ∣ μ ^ k , Σ ^ k ) α ^ k ∑ h = 1 K ϕ ( x i ∣ μ h ^ , Σ ^ h ) α ^ h \begin{align*} P(Z_i = k \mid \boldsymbol{x}_i ; \hat{\Theta}) &= \frac{p(\boldsymbol{x}_i \mid Z_i = k ; \hat{\Theta})P(Z_i = k; \hat{\Theta})}{\sum_{h=1}^K p(\boldsymbol{x}_i \mid Z_i = h ; \hat{\Theta})P(Z_i = h; \hat{\Theta})} \\ &= \frac{\phi(\boldsymbol{x}_i \mid \hat{\boldsymbol{\mu}}_k, \hat{\boldsymbol{\Sigma}}_k) \hat{\alpha}_k}{\sum_{h=1}^K \phi(\boldsymbol{x}_i \mid \hat{\boldsymbol{\mu}_h}, \hat{\boldsymbol{\Sigma}}_h) \hat{\alpha}_h} \end{align*} P ( Z i = k ∣ x i ; Θ ^ ) = ∑ h = 1 K p ( x i ∣ Z i = h ; Θ ^ ) P ( Z i = h ; Θ ^ ) p ( x i ∣ Z i = k ; Θ ^ ) P ( Z i = k ; Θ ^ ) = ∑ h = 1 K ϕ ( x i ∣ μ h ^ , Σ ^ h ) α ^ h ϕ ( x i ∣ μ ^ k , Σ ^ k ) α ^ k
模型 :P ( x ; θ ) = ∑ k = 1 K P ( x , z = k ; θ ) = ∑ k = 1 K P ( x ∣ z = k ; θ ) ⏟ 服从高斯分布 P ( z = k ; θ ) ⏟ 属于k类的概率 = ∑ k = 1 K α k ϕ ( x ; θ k ) P(x;\theta) = \sum_{k=1}^K P(x,z=k;\theta) = \sum_{k=1}^K \underbrace{P(x|z=k;\theta)}_{\text{服从高斯分布}} \underbrace{P(z=k;\theta)}_{\text{属于k类的概率}} \\ = \sum_{k=1}^K \alpha_k \phi(x;\theta_k) P ( x ; θ ) = k = 1 ∑ K P ( x , z = k ; θ ) = k = 1 ∑ K 服从高斯分布 P ( x ∣ z = k ; θ ) 属于 k 类的概率 P ( z = k ; θ ) = k = 1 ∑ K α k ϕ ( x ; θ k ) α k ≥ 0 , ∑ k = 1 K α k = 1 \alpha_k \geq 0, \sum_{k=1}^K \alpha_k = 1 α k ≥ 0 , ∑ k = 1 K α k = 1 θ k = ( μ k , σ k 2 ) \theta_k = (\mu_k,\sigma_k^2) θ k = ( μ k , σ k 2 ) ϕ ( x ; θ k ) = 1 2 π σ k 2 exp ( − ( x − μ k ) 2 2 σ k 2 ) \phi(x;\theta_k) = \frac{1}{\sqrt{2\pi\sigma_k^2}}\exp(-\frac{(x-\mu_k)^2}{2\sigma_k^2}) ϕ ( x ; θ k ) = 2 π σ k 2 1 exp ( − 2 σ k 2 ( x − μ k ) 2 )
策略 :Θ ^ \hat{\Theta} Θ ^ Θ ^ : = arg max Θ ∏ i = 1 N p ( x i ; Θ ) = arg max Θ ∏ i = 1 N ∑ k = 1 K α k ϕ ( x i ; θ k ) \hat{\Theta} := \argmax_{\Theta} \prod_{i=1}^N p(\boldsymbol{x}_i ; \Theta) \\ = \argmax_{\Theta} \prod_{i=1}^N \sum_{k=1}^K \alpha_k \phi(x_i;\theta_k) Θ ^ := Θ arg max i = 1 ∏ N p ( x i ; Θ ) = Θ arg max i = 1 ∏ N k = 1 ∑ K α k ϕ ( x i ; θ k )
算法 :Q ( θ , θ ( t ) ) = ∑ Z ∈ { 1 , 2... K } P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) = ∑ Z 1 , Z 2 , . . . , Z N ( ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) log ∏ i = 1 N P ( x i , z i ∣ θ ) ) = ∑ Z 1 , Z 2 , . . . , Z N ( ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) ∑ i = 1 N log P ( x i , z i ∣ θ ) ) Q(\theta,\theta^{(t)}) = \sum_{Z \in \{1,2...K\}} P(Z|X,\theta^{(t)}) \log P(X,Z|\theta) \\ = \sum_{Z_1,Z_2,...,Z_N} \bigg(\prod_{i=1}^N P(z_i|x_i,\theta^{(t)})\log \prod_{i=1}^N P(x_i,z_i|\theta) \bigg) \\ = \sum_{Z_1,Z_2,...,Z_N} \bigg(\prod_{i=1}^N P(z_i|x_i,\theta^{(t)}) \sum_{i=1}^N \log P(x_i,z_i|\theta) \bigg) Q ( θ , θ ( t ) ) = Z ∈ { 1 , 2... K } ∑ P ( Z ∣ X , θ ( t ) ) log P ( X , Z ∣ θ ) = Z 1 , Z 2 , ... , Z N ∑ ( i = 1 ∏ N P ( z i ∣ x i , θ ( t ) ) log i = 1 ∏ N P ( x i , z i ∣ θ ) ) = Z 1 , Z 2 , ... , Z N ∑ ( i = 1 ∏ N P ( z i ∣ x i , θ ( t ) ) i = 1 ∑ N log P ( x i , z i ∣ θ ) ) ∑ z 1 , z 2 , ⋯ , z N log P ( x 1 , z 1 ∣ θ ) ⋅ ∏ i = 1 N P ( z i ∣ x i , θ ( t ) ) = ∑ z 1 , z 2 , ⋯ , z N log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) ⋅ ∏ i = 2 N P ( z i ∣ x i , θ ( t ) ) = ∑ z 1 log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) ∑ z 2 , ⋯ , z N ∏ i = 2 N P ( z i ∣ x i , θ ( t ) ) = ∑ z 1 log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) ∑ z 2 P ( z 2 ∣ x 2 , θ ( t ) ) ∑ z 3 P ( z 3 ∣ x 3 , θ ( t ) ) ⋯ ∑ z N P ( z N ∣ x N , θ ( t ) ) \begin{equation*} \begin{split} &\sum_{z_1,z_2,\cdots,z_N}\log P(x_1,z_1|\theta)\cdot \prod_{i=1}^N P(z_i|x_i,\theta^{(t)})\\ =&\sum_{z_1,z_2,\cdots,z_N} \log P(x_1,z_1|\theta)\cdot P(z_1|x_1,\theta^{(t)}) \cdot \prod_{i=2}^N P(z_i|x_i,\theta^{(t)})\\ =& \sum_{z_1} \log P(x_1,z_1|\theta)\cdot P(z_1|x_1,\theta^{(t)}) \sum_{z_2,\cdots,z_N}\prod_{i=2}^N P(z_i|x_i,\theta^{(t)})\\ =& \sum_{z_1} \log P(x_1,z_1|\theta)\cdot P(z_1|x_1,\theta^{(t)}) \sum_{z_2} P(z_2|x_2,\theta^{(t)})\sum_{z_3} P(z_3|x_3,\theta^{(t)}) \cdots \sum_{z_N} P(z_N|x_N,\theta^{(t)}) \end{split}\end{equation*} = = = z 1 , z 2 , ⋯ , z N ∑ log P ( x 1 , z 1 ∣ θ ) ⋅ i = 1 ∏ N P ( z i ∣ x i , θ ( t ) ) z 1 , z 2 , ⋯ , z N ∑ log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) ⋅ i = 2 ∏ N P ( z i ∣ x i , θ ( t ) ) z 1 ∑ log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) z 2 , ⋯ , z N ∑ i = 2 ∏ N P ( z i ∣ x i , θ ( t ) ) z 1 ∑ log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) z 2 ∑ P ( z 2 ∣ x 2 , θ ( t ) ) z 3 ∑ P ( z 3 ∣ x 3 , θ ( t ) ) ⋯ z N ∑ P ( z N ∣ x N , θ ( t ) ) ∑ z i P ( z i ∣ x i , θ ( t ) ) = 1 \sum_{z_i} P(z_i|x_i,\theta^{(t)}) =1 ∑ z i P ( z i ∣ x i , θ ( t ) ) = 1 ∑ z 1 log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) \sum_{z_1} \log P(x_1,z_1|\theta)\cdot P(z_1|x_1,\theta^{(t)}) z 1 ∑ log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) Q ( θ , θ ( t ) ) = ∑ z 1 log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) + ⋯ + ∑ z N log P ( x N , z N ∣ θ ) ⋅ P ( z N ∣ x N , θ ( t ) ) = ∑ i = 1 N ∑ z i log P ( x i , z i ∣ θ ) ⋅ P ( z i ∣ x i , θ ( t ) ) \begin{equation*}\begin{split} Q(\theta, \theta^{(t)})&= \sum_{z_1} \log P(x_1,z_1|\theta)\cdot P(z_1|x_1,\theta^{(t)}) +\cdots + \sum_{z_N} \log P(x_N,z_N|\theta)\cdot P(z_N|x_N,\theta^{(t)}) \\ &=\sum_{i=1}^N \sum_{z_i} \log P(x_i,z_i|\theta)\cdot P(z_i|x_i,\theta^{(t)}) \end{split}\end{equation*} Q ( θ , θ ( t ) ) = z 1 ∑ log P ( x 1 , z 1 ∣ θ ) ⋅ P ( z 1 ∣ x 1 , θ ( t ) ) + ⋯ + z N ∑ log P ( x N , z N ∣ θ ) ⋅ P ( z N ∣ x N , θ ( t ) ) = i = 1 ∑ N z i ∑ log P ( x i , z i ∣ θ ) ⋅ P ( z i ∣ x i , θ ( t ) )
具体算法求解参考:Gaussian mixture models 以及机器学习-白板推导系列(十一)-高斯混合模型 GMM(Gaussian Mixture Model) 极大似然估计、EM 算法及高斯混合模型 EM 算法与 GMM(高斯混合聚类)Jensen 不等式和变分法两种推导 Expectation-maximization algorithm EM 算法 Mixture model Gaussian Mixture Model
变分推断 (Variational Inference )也称为变分贝叶斯(Variational Bayesian),而变分法主要是研究变分问题,即泛函的极值问题(函数的输入也是函数),根据贝叶斯公式,后验概率P ( Z ∣ X ) = P ( X ∣ Z ) P ( Z ) P ( X ) = P ( X ∣ Z ) P ( Z ) ∫ Z P ( X , Z ′ ) d Z ′ {\displaystyle P(\mathbf {Z} \mid \mathbf {X} )={\frac {P(\mathbf {X} \mid \mathbf {Z} )P(\mathbf {Z} )}{P(\mathbf {X} )}}={\frac {P(\mathbf {X} \mid \mathbf {Z} )P(\mathbf {Z} )}{\int _{\mathbf {Z} }P(\mathbf {X} ,\mathbf {Z} ')\,d\mathbf {Z} '}}} P ( Z ∣ X ) = P ( X ) P ( X ∣ Z ) P ( Z ) = ∫ Z P ( X , Z ′ ) d Z ′ P ( X ∣ Z ) P ( Z )
上面公式中的积分对于很多情况下是不可行的(所以有些模型忽略了 P(x)),要么积分没有闭式解,要么是指数级别的计算复杂度,所以很难求出后验概率,这时我们需要寻找一个简单分布q ( Z ) ≈ P ( Z ∣ X ) {\displaystyle q(\mathbf {Z} )\approx P(\mathbf {Z} \mid \mathbf {X} )} q ( Z ) ≈ P ( Z ∣ X ) q ( Z ) ^ = arg min q ( Z ) ∈ 候选的概率分布族 Q K L ( q ( Z ) ∣ P ( Z ∣ X ) ) \hat{q(Z)} = \argmin_{q(Z) \in 候选的概率分布族Q} KL(q(Z)|P(Z|X)) q ( Z ) ^ = q ( Z ) ∈ 候选的概率分布族 Q arg min K L ( q ( Z ) ∣ P ( Z ∣ X ))
我们有上面EM 算法的导出 得到log P ( X ) = D K L ( q ∥ P ) + L ( q ) {\displaystyle \log P(\mathbf {X} )=D_{\mathrm {KL} }(q\parallel P)+{\mathcal {L}}(q)} log P ( X ) = D KL ( q ∥ P ) + L ( q ) log P ( X ) ≥ L ( q ) \log P(\mathbf {X} ) \geq {\mathcal {L}}(q) log P ( X ) ≥ L ( q ) L ( q ) {\mathcal {L}}(q) L ( q ) Evidence Lower BOund,ELBO ),也就是所谓的变分函数。
KL-divergence 中有后验概率 P(Z|X),本身就是难以计算,才想找个简单分布 q(z)来近似,因此我们不能直接优化 KL-divergence,进而转化成优化 ELBOq ( Z ) ^ = arg max q ( z ) ∈ Q E L B O ( q , x ) \hat{q(Z)} = \argmax_{q(z) \in Q} ELBO(q,x) q ( Z ) ^ = q ( z ) ∈ Q arg max E L BO ( q , x )
分布族 Q 一般选择是平均场 (Mean field)分布族,即可以将 Z 拆分为多组相互独立的变量,那么q ( Z ) = ∏ m = 1 M q m ( Z m ) q({\mathbf {Z}})=\prod _{{m=1}}^{M}q_{m}({\mathbf {Z}}_{m}) q ( Z ) = m = 1 ∏ M q m ( Z m )
那么E L B O ( q , x ) = ∫ Z q ( Z ) log P ( X , Z ∣ θ ) q ( Z ) d Z = ∫ Z ( ∏ m = 1 M q m ( Z m ) ) log P ( X , Z ∣ θ ) d Z − ∫ Z ( ∏ m = 1 M q m ( Z m ) ) log ∏ m = 1 M q m ( Z m ) d Z ELBO(q,x) = \int_Zq(Z)\log \frac{P(X,Z|\theta)}{q(Z)}dZ \\ = \int_Z (\prod _{{m=1}}^{M}q_{m}({\mathbf {Z}}_{m}) ) \log P(X,Z|\theta)dZ - \int_Z (\prod _{{m=1}}^{M}q_{m}({\mathbf {Z}}_{m}) ) \log \prod _{{m=1}}^{M}q_{m}({\mathbf {Z}}_{m})dZ E L BO ( q , x ) = ∫ Z q ( Z ) log q ( Z ) P ( X , Z ∣ θ ) d Z = ∫ Z ( m = 1 ∏ M q m ( Z m )) log P ( X , Z ∣ θ ) d Z − ∫ Z ( m = 1 ∏ M q m ( Z m )) log m = 1 ∏ M q m ( Z m ) d Z
假设我们只关心其中一个子集(分量)Z j Z_j Z j q j ( Z j ) q_j(Z_j) q j ( Z j ) ∫ Z ( ∏ m = 1 M q m ( Z m ) ) ∑ m = 1 M log q m ( Z m ) d Z = ∫ Z q 1 ( Z 1 ) . q 2 ( Z 2 ) . . . q M ( Z M ) . [ log q 1 ( Z 1 ) + . . . + log q M ( Z M ) ] d Z \int_Z (\prod _{{m=1}}^{M}q_{m}({\mathbf {Z}}_{m}) ) \sum_{m=1}^M \log q_{m}({\mathbf {Z}}_{m})dZ \\ = \int_Z q_1(Z_1).q_2(Z_2)...q_M(Z_M).[\log q_1(Z_1)+...+\log q_M(Z_M)]dZ ∫ Z ( m = 1 ∏ M q m ( Z m )) m = 1 ∑ M log q m ( Z m ) d Z = ∫ Z q 1 ( Z 1 ) . q 2 ( Z 2 ) ... q M ( Z M ) . [ log q 1 ( Z 1 ) + ... + log q M ( Z M )] d Z
只看其中一项∫ Z 1 Z 2 . . . Z M q 1 ( Z 1 ) . q 2 ( Z 2 ) . . . q M ( Z M ) . log q 1 ( Z 1 ) d Z 1 d Z 2 . . . d Z M = ∫ Z 1 q 1 ( Z 1 ) . log q 1 ( Z 1 ) d Z 1 . ∫ Z 2 q 2 ( Z 2 ) d Z 2 . . . . ∫ Z M q M ( Z M ) d Z M \int_{Z_1Z_2...Z_M} q_1(Z_1).q_2(Z_2)...q_M(Z_M).\log q_1(Z_1){dZ_1dZ_2...dZ_M} = \int_{Z_1} q_1(Z_1).\log q_1(Z_1)dZ_1.\int_{Z_2}q_2(Z_2)dZ_2....\int_{Z_M}q_M(Z_M)dZ_M ∫ Z 1 Z 2 ... Z M q 1 ( Z 1 ) . q 2 ( Z 2 ) ... q M ( Z M ) . log q 1 ( Z 1 ) d Z 1 d Z 2 ... d Z M = ∫ Z 1 q 1 ( Z 1 ) . log q 1 ( Z 1 ) d Z 1 . ∫ Z 2 q 2 ( Z 2 ) d Z 2 .... ∫ Z M q M ( Z M ) d Z M
那么最终我们得到减号后面的项∑ m = 1 M ∫ Z m q m ( Z m ) . log q m ( Z m ) d Z m \sum_{m=1}^M \int_{Z_m} q_m(Z_m).\log q_m(Z_m)dZ_m m = 1 ∑ M ∫ Z m q m ( Z m ) . log q m ( Z m ) d Z m
前面说了,我们只关注其中一个子集Z j Z_j Z j m ≠ j m \neq j m = j ∫ Z j q j ( Z j ) . log q j ( Z j ) d Z j + C \int_{Z_j} q_j(Z_j).\log q_j(Z_j)dZ_j + C ∫ Z j q j ( Z j ) . log q j ( Z j ) d Z j + C
再看减号前面的项∫ Z 1 Z 2 . . . Z M ( ∏ m = 1 M q m ( Z m ) ) log P ( X , Z ∣ θ ) d Z 1 d Z 2 . . . d Z M = ∫ Z j q j ( Z j ) ( ∫ Z i ∏ i ≠ j M q i ( Z i ) log P ( X , Z ∣ θ ) d Z i ) d Z j = ∫ Z j q j ( Z j ) ( E ∏ i ≠ j M q i ( Z i ) [ log P ( X , Z ∣ θ ) ] ) d Z j = ∫ Z j q j ( Z j ) ( log p ~ ( X , Z j ) ) d Z j \int_{Z_1Z_2...Z_M} (\prod _{{m=1}}^{M}q_{m}({\mathbf {Z}}_{m}) ) \log P(X,Z|\theta){dZ_1dZ_2...dZ_M} \\= \int_{Z_j}q_j(Z_j) \bigg(\int_{Z_i} \prod_{i \neq j}^M q_i(Z_i) \log P(X,Z|\theta) dZ_i \bigg)dZ_j \\= \int_{Z_j}q_j(Z_j) \bigg(E_{\prod_{i \neq j}^M q_i(Z_i)}[\log P(X,Z|\theta)] \bigg)dZ_j \\= \int_{Z_j}q_j(Z_j) \bigg(\log \tilde{p}(X,Z_j) \bigg)dZ_j ∫ Z 1 Z 2 ... Z M ( m = 1 ∏ M q m ( Z m )) log P ( X , Z ∣ θ ) d Z 1 d Z 2 ... d Z M = ∫ Z j q j ( Z j ) ( ∫ Z i i = j ∏ M q i ( Z i ) log P ( X , Z ∣ θ ) d Z i ) d Z j = ∫ Z j q j ( Z j ) ( E ∏ i = j M q i ( Z i ) [ log P ( X , Z ∣ θ )] ) d Z j = ∫ Z j q j ( Z j ) ( log p ~ ( X , Z j ) ) d Z j
最终:E L B O ( q , x ) = ∫ Z j q j ( Z j ) ( log p ~ ( X , Z j ) ) d Z j − ∫ Z j q j ( Z j ) . log q j ( Z j ) d Z j − C = − K L ( q j ( Z j ) ∥ p ~ ( X , Z j ) ) − C ELBO(q,x) =\int_{Z_j}q_j(Z_j) \bigg(\log \tilde{p}(X,Z_j) \bigg)dZ_j - \int_{Z_j} q_j(Z_j).\log q_j(Z_j)dZ_j - C \\= -KL(q_j(Z_j) \| \tilde{p}(X,Z_j)) -C E L BO ( q , x ) = ∫ Z j q j ( Z j ) ( log p ~ ( X , Z j ) ) d Z j − ∫ Z j q j ( Z j ) . log q j ( Z j ) d Z j − C = − K L ( q j ( Z j ) ∥ p ~ ( X , Z j )) − C arg max E L B O ( q , x ) = arg min K L ( q j ( Z j ) ∥ p ~ ( X , Z j ) ) \argmax ELBO(q,x) = \argmin KL(q_j(Z_j) \| \tilde{p}(X,Z_j)) arg max E L BO ( q , x ) = arg min K L ( q j ( Z j ) ∥ p ~ ( X , Z j )) q j ( Z j ) = p ~ ( X , Z j ) q_j(Z_j) = \tilde{p}(X,Z_j) q j ( Z j ) = p ~ ( X , Z j )
具体求最优算法这里不做介绍,可以参考变分推断(二)—— 进阶 以及 【一文学会】变分推断及其求解方法
参考11.4 节变分推断
[9-1] Dempster AP,Laird NM,Rubin DB. Maximum-likelihood from incomplete data via theEM algorithm. J. Royal Statist. Soc. Ser. B.,1977,39
[9-2] Hastie T,Tibshirani R,Friedman J. The Elements of Statistical Learning: DataMining,Inference,and Prediction. Springer-Verlag,2001(中译本:统计学习基础——数据挖掘、推理与预测。范明,柴玉梅,昝红英等译。北京:电子工业出版社,2004)
[9-3] McLachlan G,Krishnan T. The EM Algorithm and Extensions. New York: John Wiley& Sons,1996
[9-4] 茆诗松,王静龙,濮晓龙。高等数理统计。北京:高等教育出版社;海登堡:斯普林格出版社,1998
[9-5] Wu CFJ. On the convergence properties of the EM algorithm. The Annals ofStatistics,1983,11: 95–103
[9-6] Radford N,Geoffrey H,Jordan MI. A view of the EM algorithm that justifiesincremental,sparse,and other variants. In: Learning in Graphical Models. Cambridge,MA: MITPress,1999,355–368
隐马尔可夫模型 (Hidden Markov Model,HMM )是可用于标注问题 的统计学习模型,描述由隐藏的马尔可夫链随机生成观测序列的过程,属于生成模型。
马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列 ,再由各个状态生成一个观测而产生观测随机序列的过程。状态序列 (state sequence);每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列 (observation sequence)。序列的每一个位置又可以看作是一个时刻。
隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。Q = { q 1 , q 2 , . . . , q N } , V = { v 1 , v 2 , . . . , v M } Q = \{q_1,q_2,...,q_N\} , V= \{v_1,v_2,...,v_M\} Q = { q 1 , q 2 , ... , q N } , V = { v 1 , v 2 , ... , v M } I = ( i 1 , i 2 , . . . , i T ) I = (i_1,i_2,...,i_T) I = ( i 1 , i 2 , ... , i T ) O = ( o 1 , o 2 , . . . , o T ) O = (o_1,o_2,...,o_T) O = ( o 1 , o 2 , ... , o T )
状态转移矩阵(状态转移概率分布) :(就是初始化参数transmat_prior ,也可以用 params 和求出的属性 transmat_)A = [ a i j ] N × N A=[a_{ij}]_{N\times N} A = [ a ij ] N × N a i j = P ( i _ t + 1 = q j ∣ i t = q i ) , 下标 i , j = 1 , . . . , N a_{ij} = P(i\_{t+1} = q_j | i_t = q_i) ,下标 i,j = 1,...,N a ij = P ( i _ t + 1 = q j ∣ i t = q i ) , 下标 i , j = 1 , ... , N t t t q i q_i q i t + 1 t+1 t + 1 q j q_j q j
观测矩阵(观测概率分布) :(对于 MultinomialHMM 用 params 和求出的属性 emissionprob_,叫发生概率矩阵;对于 GMMHMM 有 n_mix 、means_prior、covars_prior ;对于 GaussianHMM 有 means_prior、covars_prior )B = [ b j ( k ) ] N × M B = [b_j(k)]_{N \times M} B = [ b j ( k ) ] N × M b j ( k ) = P ( o t = v k ∣ i t = q j ) , k = 1 , . . . , M , j = 1 , . . . , N b_j(k) = P(o_t = v_k | i_t = q_j) ,k = 1,...,M,j = 1,...,N b j ( k ) = P ( o t = v k ∣ i t = q j ) , k = 1 , ... , M , j = 1 , ... , N t t t q j q_j q j v k v_k v k
初始状态概率向量(初始概率分布) :(就是初始化参数startprob_prior 和求出的属性 startprob_ )π = ( π i ) \pi = (\pi_i) π = ( π i ) π i = P ( i 1 = q i ) , 下标 i = 1 , . . . , N \pi_i = P(i_1 =q_i) ,下标i = 1,...,N π i = P ( i 1 = q i ) , 下标 i = 1 , ... , N t = 1 t=1 t = 1 q i q_i q i
隐马尔可夫模型由初始状态概率向量π \pi π A A A B B B π \pi π A A A B B B 一个隐马尔可夫模型 可以用三元符号表示,即λ = ( A , B , π ) \lambda = (A,B,\pi) λ = ( A , B , π )
状态转移概率矩阵A A A π \pi π B B B
从定义可知,隐马尔可夫模型作了两个基本假设 :
齐次马尔可夫性假设 ,即假设隐藏的马尔可夫链在任意时刻 t 的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻 t 无关。P ( i t ∣ i t − 1 , o t − 1 , . . . , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) , t = 1 , 2 , . . . , T P(i_{t}|i_{t-1},o_{t-1},...,i_{1},o_{1}) = P(i_{t}|i_{t-1}), t=1,2,...,T P ( i t ∣ i t − 1 , o t − 1 , ... , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) , t = 1 , 2 , ... , T 观测独立性假设 ,即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关。P ( o t ∣ i T , o T , i T − 1 , o T − 1 , . . . , i t + 1 , o t + 1 , i t , o t , i t − 1 , o t − 1 , . . . , i 1 , o 1 ) = P ( o t ∣ i t ) P(o_{t}|i_{T},o_{T},i_{T-1},o_{T-1},...,i_{t+1},o_{t+1},i_{t},o_{t},i_{t-1},o_{t-1},...,i_{1},o_{1}) = P(o_{t}|i_{t}) P ( o t ∣ i T , o T , i T − 1 , o T − 1 , ... , i t + 1 , o t + 1 , i t , o t , i t − 1 , o t − 1 , ... , i 1 , o 1 ) = P ( o t ∣ i t )
隐马尔可夫模型的三个基本问题 :
概率计算问题。给定模型λ = ( A , B , π ) \lambda = (A,B,\pi) λ = ( A , B , π ) O = ( o 1 , o 2 , . . . , o T ) O = (o_1,o_2,...,o_T) O = ( o 1 , o 2 , ... , o T ) λ \lambda λ O O O P ( O ∣ λ ) P(O|\lambda) P ( O ∣ λ )
学习问题。已知观测序列O = ( o 1 , o 2 , . . . , o T ) O = (o_1,o_2,...,o_T) O = ( o 1 , o 2 , ... , o T ) λ = ( A , B , π ) \lambda = (A,B,\pi) λ = ( A , B , π ) P ( O ∣ λ ) P(O|\lambda) P ( O ∣ λ ) λ M L E = arg max λ P ( O ∣ λ ) \lambda_{MLE}=\argmax_{\lambda}P(O|\lambda) λ M L E = arg max λ P ( O ∣ λ )
预测问题,也称为解码(decoding)问题。已知模型λ = ( A , B , π ) \lambda = (A,B,\pi) λ = ( A , B , π ) O = ( o 1 , o 2 , . . . , o T ) O = (o_1,o_2,...,o_T) O = ( o 1 , o 2 , ... , o T ) P ( I ∣ O ) P(I|O) P ( I ∣ O ) I = ( i 1 , i 2 , . . . , i T ) I = (i_1,i_2,...,i_T) I = ( i 1 , i 2 , ... , i T ) I ^ = arg max I P ( I ∣ O , λ ) \hat{I}=\argmax_{I}P(I|O,\lambda) I ^ = arg max I P ( I ∣ O , λ )
概率计算问题 :P ( O ∣ λ ) , P ( O ; λ ) P(O|\lambda),P(O;\lambda) P ( O ∣ λ ) , P ( O ; λ ) λ \lambda λ P ( O ∣ λ ) = ∑ I P ( O , I ∣ λ ) = ∑ I P ( O ∣ I , λ ) P ( I ∣ λ ) P(O|\lambda) = \sum_{I}P(O,I|\lambda)= \sum_{I}P(O|I,\lambda)P(I|\lambda) P ( O ∣ λ ) = I ∑ P ( O , I ∣ λ ) = I ∑ P ( O ∣ I , λ ) P ( I ∣ λ ) P ( i 1 ∣ λ ) = P ( i 1 ) P(i_1|\lambda) = P(i_1) P ( i 1 ∣ λ ) = P ( i 1 ) P ( I ∣ λ ) = P ( i 1 , i 2 , . . . , i T ∣ λ ) = P ( i 1 ) . P ( i 2 ∣ i 1 , λ ) . P ( i 3 ∣ i 1 , i 2 , λ ) . . . P ( i T ∣ i 1 , i 2 , . . . , i T − 1 , λ ) = P ( i 1 ) ∏ t = 2 T P ( i t ∣ i 1 , i 2 , . . . , i t − 1 , λ ) = P ( i 1 ) ∏ t = 2 T P ( i t ∣ i t − 1 , λ ) = π i 1 ∏ t = 2 T a i t − 1 i t P(I|\lambda) = P(i_1,i_2,...,i_T|\lambda)=P(i_1).P(i_2|i_1,\lambda).P(i_3|i_1,i_2,\lambda)...P(i_T|i_1,i_2,...,i_{T-1},\lambda) \\= P(i_1)\prod_{t=2}^T P(i_t|i_1,i_2,...,i_{t-1},\lambda) \\= P(i_1)\prod_{t=2}^T P(i_t|i_{t-1},\lambda) \\= \pi_{i_1}\prod_{t=2}^T a_{i_{t-1}i_{t}} P ( I ∣ λ ) = P ( i 1 , i 2 , ... , i T ∣ λ ) = P ( i 1 ) . P ( i 2 ∣ i 1 , λ ) . P ( i 3 ∣ i 1 , i 2 , λ ) ... P ( i T ∣ i 1 , i 2 , ... , i T − 1 , λ ) = P ( i 1 ) t = 2 ∏ T P ( i t ∣ i 1 , i 2 , ... , i t − 1 , λ ) = P ( i 1 ) t = 2 ∏ T P ( i t ∣ i t − 1 , λ ) = π i 1 t = 2 ∏ T a i t − 1 i t P ( O ∣ I , λ ) = P ( o 1 , o 2 , . . . , o T ∣ i 1 , i 2 , . . . , i T , λ ) = P ( o 1 ∣ i 1 , i 2 , . . . , i T , λ ) . P ( o 2 ∣ o 1 , i 1 , i 2 , . . . , i T , λ ) . P ( o 3 ∣ o 1 , o 2 , i 1 , i 2 , . . . , i T , λ ) . . . P ( o T ∣ o 1 , o 2 , . . . , o T − 1 , i 1 , i 2 , . . . , i T , λ ) = P ( o 1 ∣ i 1 , λ ) . P ( o 2 ∣ i 2 , λ ) . . . P ( o T ∣ i T , λ ) = ∏ t = 1 T b i t ( o t ) P(O|I,\lambda) = P(o_1,o_2,...,o_T|i_1,i_2,...,i_{T},\lambda) \\= P(o_1|i_1,i_2,...,i_{T},\lambda).P(o_2|o_1,i_1,i_2,...,i_{T},\lambda).P(o_3|o_1,o_2,i_1,i_2,...,i_{T},\lambda)...P(o_T|o_1,o_2,...,o_{T-1},i_1,i_2,...,i_{T},\lambda) \\ = P(o_1|i_1,\lambda).P(o_2|i_2,\lambda)...P(o_T|i_T,\lambda) \\= \prod_{t=1}^Tb_{i_t}(o_t) P ( O ∣ I , λ ) = P ( o 1 , o 2 , ... , o T ∣ i 1 , i 2 , ... , i T , λ ) = P ( o 1 ∣ i 1 , i 2 , ... , i T , λ ) . P ( o 2 ∣ o 1 , i 1 , i 2 , ... , i T , λ ) . P ( o 3 ∣ o 1 , o 2 , i 1 , i 2 , ... , i T , λ ) ... P ( o T ∣ o 1 , o 2 , ... , o T − 1 , i 1 , i 2 , ... , i T , λ ) = P ( o 1 ∣ i 1 , λ ) . P ( o 2 ∣ i 2 , λ ) ... P ( o T ∣ i T , λ ) = t = 1 ∏ T b i t ( o t )
P ( O , I ∣ λ ) = P ( O ∣ I , λ ) P ( I ∣ λ ) = π i 1 ∏ t = 2 T a i t − 1 i t ∏ t = 1 T b i t ( o t ) = π i 1 b i 1 ( o 1 ) . a i 1 i 2 b i 2 ( o 2 ) . . . a i T − 1 i T b i T ( o T ) = π i 1 b i 1 ( o 1 ) ∏ t = 2 T a i t − 1 i t b i t ( o t ) P(O,I|\lambda) = P(O|I,\lambda)P(I|\lambda) = \pi_{i_1}\prod_{t=2}^T a_{i_{t-1}i_{t}}\prod_{t=1}^Tb_{i_t}(o_t)
\\= \pi_{i_1}b_{i_1}(o_1) .a_{i_1i_2}b_{i_2}(o_2)...a_{i_{T-1}i_T}b_{i_T}(o_T) = \pi_{i_1}b_{i_1}(o_1)\prod_{t=2}^T a_{i_{t-1}i_{t}}b_{i_t}(o_t) P ( O , I ∣ λ ) = P ( O ∣ I , λ ) P ( I ∣ λ ) = π i 1 t = 2 ∏ T a i t − 1 i t t = 1 ∏ T b i t ( o t ) = π i 1 b i 1 ( o 1 ) . a i 1 i 2 b i 2 ( o 2 ) ... a i T − 1 i T b i T ( o T ) = π i 1 b i 1 ( o 1 ) t = 2 ∏ T a i t − 1 i t b i t ( o t )
概率计算问题- 直接由上面计算概率 可得P ( O ∣ λ ) = ∑ I P ( O , I ∣ λ ) = ∑ I P ( O ∣ I , λ ) P ( I ∣ λ ) = ∑ i 1 , i 2 , . . . , i T π i 1 b i 1 ( o 1 ) ∏ t = 2 T a i t − 1 i t b i t ( o t ) = ∑ i 1 ∈ N . . . ∑ i T ∈ N π i 1 b i 1 ( o 1 ) ∏ t = 2 T a i t − 1 i t b i t ( o t ) P(O|\lambda) = \sum_{I}P(O,I|\lambda)= \sum_{I}P(O|I,\lambda)P(I|\lambda) \\= \sum_{i_1,i_2,...,i_T} \pi_{i_1}b_{i_1}(o_1)\prod_{t=2}^T a_{i_{t-1}i_{t}}b_{i_t}(o_t) \\= \sum_{i_1 \in N}...\sum_{i_T\in N} \pi_{i_1}b_{i_1}(o_1)\prod_{t=2}^T a_{i_{t-1}i_{t}}b_{i_t}(o_t) P ( O ∣ λ ) = I ∑ P ( O , I ∣ λ ) = I ∑ P ( O ∣ I , λ ) P ( I ∣ λ ) = i 1 , i 2 , ... , i T ∑ π i 1 b i 1 ( o 1 ) t = 2 ∏ T a i t − 1 i t b i t ( o t ) = i 1 ∈ N ∑ ... i T ∈ N ∑ π i 1 b i 1 ( o 1 ) t = 2 ∏ T a i t − 1 i t b i t ( o t ) O ( T N T ) O(TN^{T}) O ( T N T )
上面说过直接求不好求,有以下方法可求得:概率计算问题- 前向计算 :前向概率 α t ( i ) = P ( o 1 , o 2 , . . . , o t , i t = q i ∣ λ ) \alpha_t(i) = P(o_1,o_2,...,o_t,i_t=q_i | \lambda) α t ( i ) = P ( o 1 , o 2 , ... , o t , i t = q i ∣ λ ) t t t o 1 , o 2 , . . . , o t o_1,o_2,...,o_t o 1 , o 2 , ... , o t q i q_i q i P ( O ∣ λ ) = ∑ i = 1 N P ( O , i T = q i ∣ λ ) = ∑ i = 1 N P ( o 1 , . . . , o T , i T = q i ∣ λ ) = ∑ i = 1 N α T ( i ) P(O|\lambda) = \sum_{i=1}^N P(O,i_T=q_i|\lambda) = \sum_{i=1}^N P(o_1,...,o_T,i_T=q_i|\lambda) = \sum_{i=1}^N \alpha_T(i) P ( O ∣ λ ) = i = 1 ∑ N P ( O , i T = q i ∣ λ ) = i = 1 ∑ N P ( o 1 , ... , o T , i T = q i ∣ λ ) = i = 1 ∑ N α T ( i )
其实P ( O ∣ λ ) = ∑ j = 1 N P ( O , i 1 = q j ∣ λ ) = . . . = ∑ j = 1 N P ( O , i t = q j ∣ λ ) = ∑ i = 1 N ∑ j = 1 N P ( O , i 1 = q i , i 2 = q j ∣ λ ) P(O|\lambda) = \sum_{j=1}^N P(O,i_1=q_j|\lambda) =...= \sum_{j=1}^N P(O,i_t=q_j|\lambda) = \sum_{i=1}^N\sum_{j=1}^N P(O,i_1=q_i,i_2=q_j|\lambda) P ( O ∣ λ ) = ∑ j = 1 N P ( O , i 1 = q j ∣ λ ) = ... = ∑ j = 1 N P ( O , i t = q j ∣ λ ) = ∑ i = 1 N ∑ j = 1 N P ( O , i 1 = q i , i 2 = q j ∣ λ ) O = ( o 1 , . . . , o T ) O=(o_1,...,o_T) O = ( o 1 , ... , o T )
所以我们只要求出α T ( i ) \alpha_T(i) α T ( i ) α 1 ( i ) . . . α t + 1 ( i ) . . . α T ( i ) \alpha_1(i) ... \alpha_{t+1}(i) ... \alpha_T(i) α 1 ( i ) ... α t + 1 ( i ) ... α T ( i )
α 1 ( i ) = P ( o 1 , i 1 = q i ∣ λ ) = P ( i 1 = q i ∣ λ ) P ( o 1 ∣ i 1 = q i , λ ) = π i b i ( o 1 ) ⋮ α t + 1 ( i ) = P ( o 1 , o 2 , . . . , o t , o t + 1 , i t + 1 = q i ∣ λ ) = ∑ j = 1 N P ( o 1 , o 2 , . . . , o t , o t + 1 , i t + 1 = q i , i t = q j ∣ λ ) = ∑ j = 1 N P ( o t + 1 ∣ o 1 , . . , o t , i t + 1 = q i , i t = q j , λ ) P ( o 1 , o 2 , . . . , o t , i t + 1 = q i , i t = q j ∣ λ ) = ∑ j = 1 N P ( o t + 1 ∣ i t + 1 = q i ) P ( o 1 , o 2 , . . . , o t , i t + 1 = q i , i t = q j ∣ λ ) = ∑ j = 1 N P ( o t + 1 ∣ i t + 1 = q i ) P ( i t + 1 = q i ∣ o 1 , o 2 , . . . , o t , i t = q j , λ ) P ( o 1 , o 2 , . . . , o t , i t = q j ∣ λ ) = ∑ j = 1 N P ( o t + 1 ∣ i t + 1 = q i ) P ( i t + 1 = q i ∣ i t = q j , λ ) P ( o 1 , o 2 , . . . , o t , i t = q j ∣ λ ) = ∑ j = 1 N P ( o t + 1 ∣ i t + 1 = q i ) P ( i t + 1 = q i ∣ i t = q j , λ ) α t ( j ) = P ( o t + 1 ∣ i t + 1 = q i ) ∑ j = 1 N P ( i t + 1 = q i ∣ i t = q j , λ ) α t ( j ) = [ ∑ j = 1 N α t ( j ) a j i ] b i ( o t + 1 ) \alpha_1(i) = P(o_1,i_1=q_i | \lambda) =P(i_1=q_i | \lambda)P(o_1|i_1=q_i , \lambda) = \pi_ib_i(o_1) \\ \vdots\\ \alpha_{t+1}(i) = P(o_1,o_2,...,o_t,o_{t+1},i_{t+1}=q_i | \lambda) \\=\sum_{j=1}^N P(o_1,o_2,...,o_t,o_{t+1},i_{t+1}=q_i,i_{t}=q_j | \lambda) \\ =\sum_{j=1}^NP(o_{t+1}|o_1,..,o_t,i_{t+1}=q_i,i_{t}=q_j,\lambda)P(o_1,o_2,...,o_t,i_{t+1}=q_i,i_{t}=q_j | \lambda) \\=\sum_{j=1}^NP(o_{t+1}|i_{t+1}=q_i)P(o_1,o_2,...,o_t,i_{t+1}=q_i,i_{t}=q_j | \lambda) \\= \sum_{j=1}^NP(o_{t+1}|i_{t+1}=q_i)P(i_{t+1}=q_i | o_1,o_2,...,o_t,i_{t}=q_j,\lambda)P(o_1,o_2,...,o_t,i_{t}=q_j | \lambda) \\=\sum_{j=1}^NP(o_{t+1}|i_{t+1}=q_i)P(i_{t+1}=q_i | i_{t}=q_j,\lambda)P(o_1,o_2,...,o_t,i_{t}=q_j | \lambda) \\=\sum_{j=1}^NP(o_{t+1}|i_{t+1}=q_i)P(i_{t+1}=q_i | i_{t}=q_j,\lambda)\alpha_t(j) \\= P(o_{t+1}|i_{t+1}=q_i)\sum_{j=1}^NP(i_{t+1}=q_i | i_{t}=q_j,\lambda)\alpha_t(j) \\= \bigg[\sum_{j=1}^N\alpha_t(j)a_{ji} \bigg] b_i(o_{t+1}) α 1 ( i ) = P ( o 1 , i 1 = q i ∣ λ ) = P ( i 1 = q i ∣ λ ) P ( o 1 ∣ i 1 = q i , λ ) = π i b i ( o 1 ) ⋮ α t + 1 ( i ) = P ( o 1 , o 2 , ... , o t , o t + 1 , i t + 1 = q i ∣ λ ) = j = 1 ∑ N P ( o 1 , o 2 , ... , o t , o t + 1 , i t + 1 = q i , i t = q j ∣ λ ) = j = 1 ∑ N P ( o t + 1 ∣ o 1 , .. , o t , i t + 1 = q i , i t = q j , λ ) P ( o 1 , o 2 , ... , o t , i t + 1 = q i , i t = q j ∣ λ ) = j = 1 ∑ N P ( o t + 1 ∣ i t + 1 = q i ) P ( o 1 , o 2 , ... , o t , i t + 1 = q i , i t = q j ∣ λ ) = j = 1 ∑ N P ( o t + 1 ∣ i t + 1 = q i ) P ( i t + 1 = q i ∣ o 1 , o 2 , ... , o t , i t = q j , λ ) P ( o 1 , o 2 , ... , o t , i t = q j ∣ λ ) = j = 1 ∑ N P ( o t + 1 ∣ i t + 1 = q i ) P ( i t + 1 = q i ∣ i t = q j , λ ) P ( o 1 , o 2 , ... , o t , i t = q j ∣ λ ) = j = 1 ∑ N P ( o t + 1 ∣ i t + 1 = q i ) P ( i t + 1 = q i ∣ i t = q j , λ ) α t ( j ) = P ( o t + 1 ∣ i t + 1 = q i ) j = 1 ∑ N P ( i t + 1 = q i ∣ i t = q j , λ ) α t ( j ) = [ j = 1 ∑ N α t ( j ) a ji ] b i ( o t + 1 )
概率计算问题- 后向计算 :后向概率 β t ( i ) = P ( o t + 1 , o t + 2 , . . . , o T ∣ i t = q i , λ ) \beta_t(i) = P(o_{t+1},o_{t+2},...,o_T|i_t=q_i , \lambda) β t ( i ) = P ( o t + 1 , o t + 2 , ... , o T ∣ i t = q i , λ ) q i q_i q i t + 1 t+1 t + 1 T T T o t + 1 , o t + 2 , . . . , o T o_{t+1},o_{t+2},...,o_T o t + 1 , o t + 2 , ... , o T P ( O ∣ λ ) = ∑ i = 1 N P ( O , i 1 = q i ∣ λ ) = ∑ i = 1 N P ( o 1 , . . . , o T , i 1 = q i ∣ λ ) = ∑ i = 1 N P ( o 1 , . . . , o T ∣ i 1 = q i , λ ) P ( i 1 = q i ∣ λ ) = ∑ i = 1 N P ( o 1 ∣ o 2 , . . . , o T , i 1 = q i , λ ) P ( o 2 , . . . , o T ∣ i 1 = q i , λ ) P ( i 1 = q i ∣ λ ) = ∑ i = 1 N P ( o 1 ∣ i 1 = q i , λ ) P ( o 2 , . . . , o T ∣ i 1 = q i , λ ) P ( i 1 = q i ∣ λ ) = ∑ i = 1 N b i ( o 1 ) β 1 ( i ) π i P(O|\lambda) = \sum_{i=1}^N P(O,i_1=q_i|\lambda) = \sum_{i=1}^N P(o_1,...,o_T,i_1=q_i|\lambda) \\= \sum_{i=1}^N P(o_1,...,o_T|i_1=q_i,\lambda)P(i_1=q_i|\lambda) \\= \sum_{i=1}^N P(o_1|o_2,...,o_T,i_1=q_i,\lambda)P(o_2,...,o_T|i_1=q_i,\lambda)P(i_1=q_i|\lambda) \\ = \sum_{i=1}^N P(o_1|i_1=q_i,\lambda)P(o_2,...,o_T|i_1=q_i,\lambda)P(i_1=q_i|\lambda) \\= \sum_{i=1}^N b_i(o_1)\beta_1(i)\pi_i P ( O ∣ λ ) = i = 1 ∑ N P ( O , i 1 = q i ∣ λ ) = i = 1 ∑ N P ( o 1 , ... , o T , i 1 = q i ∣ λ ) = i = 1 ∑ N P ( o 1 , ... , o T ∣ i 1 = q i , λ ) P ( i 1 = q i ∣ λ ) = i = 1 ∑ N P ( o 1 ∣ o 2 , ... , o T , i 1 = q i , λ ) P ( o 2 , ... , o T ∣ i 1 = q i , λ ) P ( i 1 = q i ∣ λ ) = i = 1 ∑ N P ( o 1 ∣ i 1 = q i , λ ) P ( o 2 , ... , o T ∣ i 1 = q i , λ ) P ( i 1 = q i ∣ λ ) = i = 1 ∑ N b i ( o 1 ) β 1 ( i ) π i β 1 ( i ) \beta_1(i) β 1 ( i ) β T ( i ) . . . β 1 t − 1 ( i ) . . . β 1 ( i ) \beta_T(i) ... \beta_1{t-1}(i) ... \beta_1(i) β T ( i ) ... β 1 t − 1 ( i ) ... β 1 ( i )
β T ( i ) = P ( i T = q i , λ ) = 1 ⋮ β t ( i ) = P ( o t + 1 , o t + 2 , . . . , o T ∣ i t = q i , λ ) = ∑ j = 1 N P ( o t + 1 , o t + 2 , . . . , o T , i t + 1 = q j ∣ i t = q i , λ ) = ∑ j = 1 N P ( o t + 1 , o t + 2 , . . . , o T ∣ i t + 1 = q j , i t = q i , λ ) P ( i t + 1 = q j ∣ i t = q i , λ ) 条件前面没有 o t ( 根据概率图也能得出给定 i t + 1 时, i t 与 o t + 1 , . . . , o T 无关 ) = ∑ j = 1 N P ( o t + 1 , o t + 2 , . . . , o T ∣ i t + 1 = q j , λ ) P ( i t + 1 = q j ∣ i t = q i , λ ) = ∑ j = 1 N P ( o t + 1 ∣ o t + 2 , . . . , o T , i t + 1 = q j , λ ) P ( o t + 2 , . . . , o T ∣ i t + 1 = q j , λ ) P ( i t + 1 = q j ∣ i t = q i , λ ) = ∑ j = 1 N P ( o t + 1 ∣ i t + 1 = q j , λ ) P ( o t + 2 , . . . , o T ∣ i t + 1 = q j , λ ) P ( i t + 1 = q j ∣ i t = q i , λ ) = ∑ j = 1 N b j ( o t + 1 ) β t + 1 ( j ) a i j \beta_T(i) = P(i_T = q_i,\lambda) = 1 \\ \vdots \\ \beta_t(i) = P(o_{t+1},o_{t+2},...,o_T|i_t=q_i , \lambda) \\= \sum_{j=1}^N P(o_{t+1},o_{t+2},...,o_T,i_{t+1}=q_j|i_t=q_i , \lambda) \\= \sum_{j=1}^N P(o_{t+1},o_{t+2},...,o_T|i_{t+1}=q_j,i_t=q_i , \lambda) P(i_{t+1}=q_j|i_t=q_i , \lambda) \\ 条件前面没有o_t(根据概率图也能得出给定i_{t+1}时,i_t与o_{t+1},...,o_T无关) \\= \sum_{j=1}^N P(o_{t+1},o_{t+2},...,o_T|i_{t+1}=q_j, \lambda) P(i_{t+1}=q_j|i_t=q_i , \lambda) \\= \sum_{j=1}^N P(o_{t+1}|o_{t+2},...,o_T,i_{t+1}=q_j, \lambda)P(o_{t+2},...,o_T|i_{t+1}=q_j, \lambda) P(i_{t+1}=q_j|i_t=q_i , \lambda)\\= \sum_{j=1}^N P(o_{t+1}|i_{t+1}=q_j, \lambda)P(o_{t+2},...,o_T|i_{t+1}=q_j, \lambda) P(i_{t+1}=q_j|i_t=q_i , \lambda) \\ =\sum_{j=1}^N b_j(o_{t+1}) \beta_{t+1}(j) a_{ij} β T ( i ) = P ( i T = q i , λ ) = 1 ⋮ β t ( i ) = P ( o t + 1 , o t + 2 , ... , o T ∣ i t = q i , λ ) = j = 1 ∑ N P ( o t + 1 , o t + 2 , ... , o T , i t + 1 = q j ∣ i t = q i , λ ) = j = 1 ∑ N P ( o t + 1 , o t + 2 , ... , o T ∣ i t + 1 = q j , i t = q i , λ ) P ( i t + 1 = q j ∣ i t = q i , λ ) 条件前面没有 o t ( 根据概率图也能得出给定 i t + 1 时, i t 与 o t + 1 , ... , o T 无关 ) = j = 1 ∑ N P ( o t + 1 , o t + 2 , ... , o T ∣ i t + 1 = q j , λ ) P ( i t + 1 = q j ∣ i t = q i , λ ) = j = 1 ∑ N P ( o t + 1 ∣ o t + 2 , ... , o T , i t + 1 = q j , λ ) P ( o t + 2 , ... , o T ∣ i t + 1 = q j , λ ) P ( i t + 1 = q j ∣ i t = q i , λ ) = j = 1 ∑ N P ( o t + 1 ∣ i t + 1 = q j , λ ) P ( o t + 2 , ... , o T ∣ i t + 1 = q j , λ ) P ( i t + 1 = q j ∣ i t = q i , λ ) = j = 1 ∑ N b j ( o t + 1 ) β t + 1 ( j ) a ij
模型 :P ( O ∣ λ ) = ∑ I P ( O , I ∣ λ ) = ∑ I P ( O ∣ I , λ ) P ( I ∣ λ ) P(O|\lambda) = \sum_{I}P(O,I|\lambda) = \sum_{I}P(O|I,\lambda)P(I|\lambda) P ( O ∣ λ ) = I ∑ P ( O , I ∣ λ ) = I ∑ P ( O ∣ I , λ ) P ( I ∣ λ )
策略 :arg max λ P ( O ∣ λ ) \argmax_{\lambda} P(O|\lambda) λ arg max P ( O ∣ λ )
算法 :Q ( λ , λ ˉ ) = ∑ I log P ( O , I ∣ λ ) P ( I ∣ O , λ ˉ ) = ∑ I log P ( O , I ∣ λ ) P ( I , O ∣ λ ˉ ) . 1 P ( O ∣ λ ˉ ) Q(\lambda,\={\lambda}) = \sum_{I} \log P(O,I|\lambda) P(I|O,\={\lambda}) = \sum_{I} \log P(O,I|\lambda) P(I,O|\={\lambda}).\frac{1}{P(O|\={\lambda})} Q ( λ , λ ˉ ) = I ∑ log P ( O , I ∣ λ ) P ( I ∣ O , λ ˉ ) = I ∑ log P ( O , I ∣ λ ) P ( I , O ∣ λ ˉ ) . P ( O ∣ λ ˉ ) 1 λ \lambda λ 1 / P ( O ∣ λ ˉ ) 1/{P(O|\={\lambda})} 1/ P ( O ∣ λ ˉ ) λ \lambda λ Q ( λ , λ ˉ ) = ∑ I log P ( O , I ∣ λ ) P ( I , O ∣ λ ˉ ) Q(\lambda,\={\lambda}) =\sum_{I} \log P(O,I|\lambda) P(I,O|\={\lambda}) Q ( λ , λ ˉ ) = I ∑ log P ( O , I ∣ λ ) P ( I , O ∣ λ ˉ ) P ( O , I ∣ λ ) = ∑ I π i 1 b i 1 ( o 1 ) ∏ t = 2 T a i t − 1 i t b i t ( o t ) = ∑ I π i 1 ∏ t = 2 T a i t − 1 i t ∏ t = 1 T b i t ( o t ) P(O,I|\lambda) = \sum_{I} \pi_{i_1}b_{i_1}(o_1)\prod_{t=2}^T a_{i_{t-1}i_{t}}b_{i_t}(o_t) = \sum_{I} \pi_{i_1}\prod_{t=2}^T a_{i_{t-1}i_{t}}\prod_{t=1}^T b_{i_t}(o_t) P ( O , I ∣ λ ) = I ∑ π i 1 b i 1 ( o 1 ) t = 2 ∏ T a i t − 1 i t b i t ( o t ) = I ∑ π i 1 t = 2 ∏ T a i t − 1 i t t = 1 ∏ T b i t ( o t ) Q ( λ , λ ˉ ) = ∑ I [ log π i 1 + ∑ t = 2 T log a i t − 1 i t + ∑ t = 1 T log b i t ( o t ) ] P ( I , O ∣ λ ˉ ) Q(\lambda,\={\lambda}) = \sum_{I}\bigg[ \log\pi_{i_1}+ \sum_{t=2}^T\log a_{i_{t-1}i_{t}} + \sum_{t=1}^T \log b_{i_t}(o_t) \bigg]P(I,O|\={\lambda}) Q ( λ , λ ˉ ) = I ∑ [ log π i 1 + t = 2 ∑ T log a i t − 1 i t + t = 1 ∑ T log b i t ( o t ) ] P ( I , O ∣ λ ˉ ) π \pi π 一站式解决:隐马尔可夫模型(HMM)全过程推导及实现 ),发现只有一项与π \pi π π ( t + 1 ) = arg max π Q ( λ , λ ( t ) ) = arg max π ∑ _ I [ log π i 1 P ( I , O ∣ λ ( t ) ) ] = arg max π ∑ i 1 ∑ i 2 . . . ∑ i T [ log π i 1 P ( i 1 , i 2 , . . . , i T , O ∣ λ ( t ) ) ] 我们观察一下,发现边缘分布可以只保留一项来计算 = arg max π ∑ i 1 [ log π i 1 P ( i 1 , O ∣ λ ( t ) ) ] 我们把 i 1 替换掉 = arg max π ∑ j = 1 N [ log π j P ( i 1 = q j , O ∣ λ ( t ) ) ] \pi^{(t+1)} = \argmax_{\pi} Q(\lambda,\lambda^{(t)}) \\= \argmax_{\pi} \sum\_{I}\bigg[ \log\pi_{i_1}P(I,O|\lambda^{(t)})\bigg] \\= \argmax_{\pi} \sum_{i_1}\sum_{i_2}...\sum_{i_T}\bigg[ \log\pi_{i_1}P(i_1,i_2,...,i_T,O|\lambda^{(t)})\bigg] \\ 我们观察一下,发现边缘分布 可以只保留一项来计算\\ =\argmax_{\pi} \sum_{i_1}\bigg[ \log\pi_{i_1}P(i_1,O|\lambda^{(t)})\bigg] \\ 我们把 i_1 替换掉 \\ =\argmax_{\pi} \sum_{j=1}^N \bigg[ \log\pi_{j}P(i_1 = q_j,O|\lambda^{(t)})\bigg] π ( t + 1 ) = π arg max Q ( λ , λ ( t ) ) = π arg max ∑ _ I [ log π i 1 P ( I , O ∣ λ ( t ) ) ] = π arg max i 1 ∑ i 2 ∑ ... i T ∑ [ log π i 1 P ( i 1 , i 2 , ... , i T , O ∣ λ ( t ) ) ] 我们观察一下,发现边缘分布可以只保留一项来计算 = π arg max i 1 ∑ [ log π i 1 P ( i 1 , O ∣ λ ( t ) ) ] 我们把 i 1 替换掉 = π arg max j = 1 ∑ N [ log π j P ( i 1 = q j , O ∣ λ ( t ) ) ] π = ( π 1 , . . , π N ) \pi = (\pi_1,..,\pi_N) π = ( π 1 , .. , π N ) ∑ j = 1 N π j = 1 \sum_{j=1}^N \pi_{j} =1 ∑ j = 1 N π j = 1 L ( π , γ ) = ∑ j = 1 N [ log π j P ( i 1 = q j , O ∣ λ ( t ) ) ] + γ ( ∑ j = 1 N π j − 1 ) L(\pi,\gamma) = \sum_{j=1}^N \bigg[ \log\pi_{j}P(i_1 = q_j,O|\lambda^{(t)})\bigg] + \gamma\bigg(\sum_{j=1}^N \pi_{j} -1\bigg) L ( π , γ ) = j = 1 ∑ N [ log π j P ( i 1 = q j , O ∣ λ ( t ) ) ] + γ ( j = 1 ∑ N π j − 1 ) π j \pi_j π j ∂ L ∂ π j = 1 π j P ( i 1 = q j , O ∣ λ ( t ) ) + γ = 0 \frac{\partial L}{\partial \pi_j} = \frac{1}{\pi_j}P(i_1 = q_j,O|\lambda^{(t)})+\gamma = 0 ∂ π j ∂ L = π j 1 P ( i 1 = q j , O ∣ λ ( t ) ) + γ = 0 P ( i 1 = q j , O ∣ λ ( t ) ) + γ π j = 0 P(i_1 = q_j,O|\lambda^{(t)}) + \gamma\pi_j=0 P ( i 1 = q j , O ∣ λ ( t ) ) + γ π j = 0 ∑ j = 1 N [ P ( i 1 = q j , O ∣ λ ( t ) ) + γ π j ] = 0 ⇓ P ( O ∣ λ ( t ) ) + γ = 0 \sum_{j=1}^N\bigg[P(i_1 = q_j,O|\lambda^{(t)}) + \gamma\pi_j \bigg]=0 \\ \Darr \\ P(O|\lambda^{(t)}) + \gamma = 0 j = 1 ∑ N [ P ( i 1 = q j , O ∣ λ ( t ) ) + γ π j ] = 0 ⇓ P ( O ∣ λ ( t ) ) + γ = 0 π j ( t + 1 ) = P ( i 1 = q j , O ∣ λ ( t ) ) P ( O ∣ λ ( t ) ) \pi_j^{(t+1)} = \frac{P(i_1 = q_j,O|\lambda^{(t)})}{P(O|\lambda^{(t)})} π j ( t + 1 ) = P ( O ∣ λ ( t ) ) P ( i 1 = q j , O ∣ λ ( t ) ) P ( X ∣ λ ( t ) ) P\left(X|\lambda^{\left(t\right)}\right) P ( X ∣ λ ( t ) ) α t ( i ) β t ( i ) = P ( x i , x 2 , … , x t , z t = q i ∣ λ ) P ( x T , x T − 1 , … , x t + 1 ∣ z t = q i , λ ) = P ( x i , x 2 , … , x t ∣ z t = q i , λ ) P ( x T , x T − 1 , … , x t + 1 ∣ z t = q i , λ ) P ( z t = q i ∣ λ ) = P ( x i , x 2 , … , x T ∣ z t = q i , λ ) P ( z t = q i ∣ λ ) = P ( X , z t = q i ∣ λ ) \begin{align} &\alpha_t\left(i\right)\beta_t\left(i\right)\\ &=P\left(x_i,x_2,\ldots,x_t,z_t=q_i|\lambda\right)P\left(x_T,x_{T-1},\ldots,x_{t+1}|z_t=q_i,\lambda\right)\\ &=P\left(x_i,x_2,\ldots,x_t|z_t=q_i,\lambda\right)P\left(x_T,x_{T-1},\ldots,x_{t+1}|z_t=q_i,\lambda\right)P\left(z_t=q_i|\lambda\right)\\ &=P\left(x_i,x_2,\ldots,x_T|z_t=q_i,\lambda\right)P\left(z_t=q_i|\lambda\right)\\ &=P\left(X,z_t=q_i|\lambda\right) \end{align} α t ( i ) β t ( i ) = P ( x i , x 2 , … , x t , z t = q i ∣ λ ) P ( x T , x T − 1 , … , x t + 1 ∣ z t = q i , λ ) = P ( x i , x 2 , … , x t ∣ z t = q i , λ ) P ( x T , x T − 1 , … , x t + 1 ∣ z t = q i , λ ) P ( z t = q i ∣ λ ) = P ( x i , x 2 , … , x T ∣ z t = q i , λ ) P ( z t = q i ∣ λ ) = P ( X , z t = q i ∣ λ ) π i ( t + 1 ) = α 1 ( i ) β 1 ( i ) P ( X ∣ λ ( t ) ) \pi_i^{\left(t+1\right)}=\frac{\alpha_1\left(i\right)\beta_1\left(i\right)}{P\left(X|\lambda^{\left(t\right)}\right)} π i ( t + 1 ) = P ( X ∣ λ ( t ) ) α 1 ( i ) β 1 ( i )
预测问题,也称为解码(decoding)问题 :Viterbi algorithm )实际是用动态规划解隐马尔可夫模型预测问题,即用动态规划(dynamic programming )求概率最大路径(最优路径),这里的最优路径就是最优状态序列I I I
请参考书籍和机器学习-白板推导系列(十四)-隐马尔可夫模型 HMM(Hidden Markov Model)
这一类模型需要求解的问题的大体框架为:X X X Z Z Z λ \lambda λ
{ R e p r e s e n t a t i o n Probabilistic graphical model L e a r n i n g λ M L E = a r g max λ P ( X ∣ λ ) Baum Welch Algorithm(EM) I n f e r e n c e { D e c o d i n g Z = a r g max Z P ( Z ∣ X , λ ) o r P ( z 1 , z 2 , ⋯ , z t ∣ x 1 , x 2 , ⋯ , x t , λ ) Viterbi Algorithm Prob of evidence P ( X ∣ λ ) Forward Algorithm,Backward Algorithm F i l t e r i n g P ( z t ∣ x 1 , x 2 , ⋯ , x t , λ ) (online)Forward Algorithm S m o t h i n g P ( z t ∣ x 1 , x 2 , ⋯ , x T , λ ) (offline)Forward-Backward Algorithm P r e d i c t i o n { P ( z t + 1 , z t + 2 , . . . ∣ x 1 , x 2 , ⋯ , x t , λ ) P ( x t + 1 , x t + 2 , . . . ∣ x 1 , x 2 , ⋯ , x t , λ ) } Forward Algorithm \begin{cases}
Representation & \text{Probabilistic graphical model} \\
Learning & \lambda_{MLE}=arg \underset{\lambda}{\max} P(X|\lambda) \boxed{\text{Baum Welch Algorithm(EM)}}\\
Inference & \begin{cases} Decoding & Z=arg\underset{Z}{\max}P(Z|X,\lambda) or P(z_1,z_2,\cdots,z_t|x_1,x_2,\cdots,x_t,\lambda) \boxed{\text{Viterbi Algorithm}}\\ \text{Prob of evidence} & P(X|\lambda) \boxed{\text{Forward Algorithm,Backward Algorithm}} \\ Filtering & P(z_t|x_1,x_2,\cdots,x_t,\lambda) \boxed{\text{(online)Forward Algorithm}}\\ Smothing & P(z_t|x_1,x_2,\cdots,x_T,\lambda) \boxed{\text{(offline)Forward-Backward Algorithm}}\\Prediction & \begin{Bmatrix} P(z_{t+1},z_{t+2},...|x_1,x_2,\cdots,x_t,\lambda) \\ P(x_{t+1},x_{t+2},...|x_1,x_2,\cdots,x_t,\lambda) \end{Bmatrix} \boxed{\text{Forward Algorithm}} \end{cases}\\
\end{cases} ⎩ ⎨ ⎧ R e p rese n t a t i o n L e a r nin g I n f ere n ce Probabilistic graphical model λ M L E = a r g λ max P ( X ∣ λ ) Baum Welch Algorithm(EM) ⎩ ⎨ ⎧ Deco d in g Prob of evidence F i lt er in g S m o t hin g P re d i c t i o n Z = a r g Z max P ( Z ∣ X , λ ) or P ( z 1 , z 2 , ⋯ , z t ∣ x 1 , x 2 , ⋯ , x t , λ ) Viterbi Algorithm P ( X ∣ λ ) Forward Algorithm,Backward Algorithm P ( z t ∣ x 1 , x 2 , ⋯ , x t , λ ) (online)Forward Algorithm P ( z t ∣ x 1 , x 2 , ⋯ , x T , λ ) (offline)Forward-Backward Algorithm { P ( z t + 1 , z t + 2 , ...∣ x 1 , x 2 , ⋯ , x t , λ ) P ( x t + 1 , x t + 2 , ...∣ x 1 , x 2 , ⋯ , x t , λ ) } Forward Algorithm
Filtering problem (stochastic processes) :Smoothing problem (stochastic processes)
随机过程 (Stochastic process ):
设( Ω , F , P ) (\Omega ,{\mathcal {F}},P) ( Ω , F , P ) 概率空间 (Probability space ),Ω \Omega Ω 样本空间 (sample space ), F \mathcal {F} F Sigma-algebra ),P P P Probability measure );( S , Σ ) (S,\Sigma ) ( S , Σ ) S S S { X ( t ) : t ∈ T } o r { X ( t , ω ) : t ∈ T } {\displaystyle \{X(t):t\in T\}} or {\displaystyle \{X(t,\omega ):t\in T\}} { X ( t ) : t ∈ T } or { X ( t , ω ) : t ∈ T }
其中X ( t ) X(t) X ( t ) t t t X ( t ) X(t) X ( t ) t t t ω ∈ Ω \omega \in \Omega ω ∈ Ω T T T T = { 0 , 1 , 2 , . . . } T=\{0,1,2,...\} T = { 0 , 1 , 2 , ... } T = [ a , b ] , a 可以取 0 或者 − ∞ , b 可以取 + ∞ T=[a,b] ,a可以取0或者 -\infty,b可以取+\infty T = [ a , b ] , a 可以取 0 或者 − ∞ , b 可以取 + ∞
映射X ( t , ω ) : T × Ω → R X(t,\omega):T \times \Omega \to R X ( t , ω ) : T × Ω → R X ( . , . ) X(.,.) X ( . , . ) T × Ω T \times \Omega T × Ω ∀ t ∈ T \forall t \in T ∀ t ∈ T t ∈ T t \in T t ∈ T X ( t , . ) X(t,.) X ( t , . ) Ω \Omega Ω 随机变量 ;∀ ω ∈ Ω \forall \omega \in \Omega ∀ ω ∈ Ω X ( . , ω ) : T → S X(.,\omega):T \to S X ( . , ω ) : T → S ω ∈ Ω \omega \in \Omega ω ∈ Ω 样本函数 (sample function),特别是当T T T { X ( t , ω ) : t ∈ T } {\displaystyle \{X(t,\omega ):t\in T\}} { X ( t , ω ) : t ∈ T } 样本路径 (sample path)。
参见书中第19章
马尔可夫性质 (Markov property ):随机过程 (Stochastic process )的未来状态的条件概率分布(以过去和现在值为条件)仅取决于当前状态,则随机过程具有马尔可夫性质;与此属性的过程被认为是马氏 或马尔可夫过程 (Markov process )。最著名的马尔可夫过程是马尔可夫链 (Markov chain )。布朗运动 (Brownian motion )是另一个著名的马尔可夫过程。马尔可夫过程是不具备记忆特质的(Memorylessness )
一阶 离散 P ( X n = x n ∣ X n − 1 = x n − 1 , … , X 0 = x 0 ) = P ( X n = x n ∣ X n − 1 = x n − 1 ) . {\displaystyle P(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},\dots ,X_{0}=x_{0})=P(X_{n}=x_{n}\mid X_{n-1}=x_{n-1}).} P ( X n = x n ∣ X n − 1 = x n − 1 , … , X 0 = x 0 ) = P ( X n = x n ∣ X n − 1 = x n − 1 ) .
m 阶 离散 Pr ( X n = x n ∣ X n − 1 = x n − 1 , X n − 2 = x n − 2 , … , X 1 = x 1 ) = Pr ( X n = x n ∣ X n − 1 = x n − 1 , X n − 2 = x n − 2 , … , X n − m = x n − m ) for n > m {\displaystyle {\begin{aligned}&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{1}=x_{1})\\={}&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{n-m}=x_{n-m}){\text{ for }}n>m\end{aligned}}} = Pr ( X n = x n ∣ X n − 1 = x n − 1 , X n − 2 = x n − 2 , … , X 1 = x 1 ) Pr ( X n = x n ∣ X n − 1 = x n − 1 , X n − 2 = x n − 2 , … , X n − m = x n − m ) for n > m
时间齐次 (Time-homogeneous)Pr ( X t + s = x ∣ X t + s − 1 = y ) = Pr ( X t = x ∣ X t − 1 = y ) {\displaystyle \Pr(X_{t+s}=x\mid X_{t+s-1}=y)=\Pr(X_{t}=x\mid X_{t-1}=y)} Pr ( X t + s = x ∣ X t + s − 1 = y ) = Pr ( X t = x ∣ X t − 1 = y )
马尔可夫模型 (Markov model ):
马尔可夫模型是具有马尔可夫性假设的随机过程,最简单的马尔可夫模型是马尔可夫链 (Markov chain )
.
Countable state space(对应随机过程的离散Ω \Omega Ω
Continuous or general state space(对应随机过程的连续Ω \Omega Ω
Discrete-time(对应随机过程的离散T T T
(discrete-time) Markov chain on a countable or finite state space
Markov chain on a measurable state space (for example, Harris chain)
Continuous-time(对应随机过程的连续T T T
Continuous-time Markov process or Markov jump process
Any continuous stochastic process with the Markov property (for example, the Wiener process)
令{ X n ∣ n = 1 , 2 , ⋯ } \{X_n|n=1,2,\cdots\} { X n ∣ n = 1 , 2 , ⋯ } { 0 , 1 , 2 , ⋯ } \{0,1,2,\cdots\} { 0 , 1 , 2 , ⋯ } X n = i X_n=i X n = i t t t i i i P i , j P_{i,j} P i , j 转移概率 (transition probability),表示处在i i i j j j i 0 , i 1 , ⋯ , i n − 1 , i , j i_0,i_1,\cdots,i_{n-1},i,j i 0 , i 1 , ⋯ , i n − 1 , i , j n ≥ 0 n\ge 0 n ≥ 0 P { X n + 1 = j ∣ X n = i , X n − 1 = i n − 1 , ⋯ , X 1 = i 1 , X 0 = i 0 } = P i , j P\{X_{n+1}=j|X_n=i,X_{n-1}=i_{n-1},\cdots,X_1=i_1,X_0=i_0\}=P_{i,j} P { X n + 1 = j ∣ X n = i , X n − 1 = i n − 1 , ⋯ , X 1 = i 1 , X 0 = i 0 } = P i , j 马尔可夫链 (Markov chain)。
一个随机过程{ X ( t ) : t ≥ 0 } \{X(t):t \geq 0\} { X ( t ) : t ≥ 0 } t ∈ R + t \in \mathbb{R}_+ t ∈ R + t ∈ N 0 t \in \mathbb{N}_0 t ∈ N 0
根据 P i , j P_{i,j} P i , j P i , j ≥ 0 , i , j ≥ 0 ; ∑ j = 0 ∞ P i , j = 1 , i = 0 , 1 , ⋯ P_{i,j}\ge0,\;i,j\ge0;\;\;\sum_{j=0}^\infty P_{i,j}=1,\;i=0,1,\cdots P i , j ≥ 0 , i , j ≥ 0 ; ∑ j = 0 ∞ P i , j = 1 , i = 0 , 1 , ⋯ P i , j P_{i,j} P i , j i i i j j j 转移(概率)矩阵 (transition matrix )也称为随机矩阵、概率矩阵、转移矩阵、替代矩阵或马尔可夫矩阵 :P i , j = ( P i n , i n + 1 ) = [ P 0 , 0 P 0 , 1 P 0 , 2 ⋯ P 1 , 0 P 1 , 1 P 1 , 2 ⋯ ⋮ ⋮ ⋮ P i , 0 P i , 1 P i , 2 ⋯ ⋮ ⋮ ⋮ ] \mathbf{P}_{i,j}=(P_{i_{n},i_{n+1}}) =\begin{bmatrix}P_{0,0}&P_{0,1}&P_{0,2}&\cdots\\P_{1,0}&P_{1,1}&P_{1,2}&\cdots\\\vdots&\vdots&\vdots\\P_{i,0}&P_{i,1}&P_{i,2}&\cdots\\\vdots&\vdots&\vdots\end{bmatrix} P i , j = ( P i n , i n + 1 ) = ⎣ ⎡ P 0 , 0 P 1 , 0 ⋮ P i , 0 ⋮ P 0 , 1 P 1 , 1 ⋮ P i , 1 ⋮ P 0 , 2 P 1 , 2 ⋮ P i , 2 ⋮ ⋯ ⋯ ⋯ ⎦ ⎤ 转移概率 P i , j n P_{i,j}^n P i , j n P i , j n = P { X n + k = j ∣ X k = i } , n ≥ 0 , i , j ≥ 0 P_{i,j}^n=P\{X_{n+k=j}|X_k=i\},\;n\ge 0,i,j\ge 0 P i , j n = P { X n + k = j ∣ X k = i } , n ≥ 0 , i , j ≥ 0
右随机矩阵 是一个非负实数的方阵,每个行总和为 1。左随机矩阵 是一个非负实数的方阵,每个列的总和为 1。双随机矩阵 是一个非负实数的方阵,每个行和每个列的总和为 1。
假设A A A
矩阵A A A A k A^k A k
至少有一个特征值为 1,其特征值在[-1,1]区间,特征值为 1 对应的特征向量π \pi π 平稳概率向量 (stationary probability vector)。
对于任意概率向量 (Probability vector )或者随机向量 π 0 \pi_0 π 0 lim k → ∞ A k π 0 = π \lim_{k \to \infty} A^k \pi_0 = \pi lim k → ∞ A k π 0 = π
对于任意概率向量 μ 0 \mu_0 μ 0 μ 1 = A μ 0 \mu_1 = A \mu_0 μ 1 = A μ 0
特征值的求解:det ( A − λ I ) = 0 \det(A-\lambda I)=0 det ( A − λ I ) = 0
由于 A A A A − I A−I A − I A − I A−I A − I det ( A − I ) = 0 \det(A-I)=0 det ( A − I ) = 0 A − I A−I A − I A A A
对角化 A = P Λ P − 1 A = P \Lambda P^{-1} A = P Λ P − 1 Λ \Lambda Λ A A A μ k = A k μ 0 = ( P Λ P − 1 ) k μ 0 = P Λ k P − 1 μ 0 \mu_k = A^k \mu_0 = (P \Lambda P^{-1})^k \mu_0 = P \Lambda^k P^{-1} \mu_0 μ k = A k μ 0 = ( P Λ P − 1 ) k μ 0 = P Λ k P − 1 μ 0 A A A x 1 , . . . , x n {x_1},...,{x_n} x 1 , ... , x n λ 1 , . . . , λ n \lambda_1,...,\lambda_n λ 1 , ... , λ n μ 0 = c 1 x 1 + ⋯ + c n x n \mu_0 = c_1{x_1} + \cdots + c_n{x_n} μ 0 = c 1 x 1 + ⋯ + c n x n A k μ 0 = A k c 1 x 1 + ⋯ + A k c n x n = c 1 A k x 1 + ⋯ + c n A k x n = c 1 A k − 1 A x 1 + ⋯ + c n A k − 1 A x n = c 1 A k − 1 λ 1 x 1 + ⋯ + c n A k − 1 λ n x n = c 1 λ 1 k x 1 + ⋯ + c n λ n k x n = ∑ i = 1 n c i λ i k x i A^k\mathbf{\mu_0} = A^kc_1\mathbf{x_1} + \cdots + A^kc_n\mathbf{x_n}\\ = c_1A^k\mathbf{x_1} + \cdots + c_nA^k\mathbf{x_n} \\= c_1A^{k-1}A\mathbf{x_1} + \cdots + c_nA^{k-1}A\mathbf{x_n} \\= c_1A^{k-1}\lambda_1\mathbf{x_1} + \cdots + c_nA^{k-1}\lambda_n\mathbf{x_n}\\=c_1\lambda_1^k\mathbf{x_1} + \cdots + c_n\lambda_n^k\mathbf{x_n}\\=\sum_{i=1}^n{c_i\lambda_i^k\bm{x_i}} A k μ 0 = A k c 1 x 1 + ⋯ + A k c n x n = c 1 A k x 1 + ⋯ + c n A k x n = c 1 A k − 1 A x 1 + ⋯ + c n A k − 1 A x n = c 1 A k − 1 λ 1 x 1 + ⋯ + c n A k − 1 λ n x n = c 1 λ 1 k x 1 + ⋯ + c n λ n k x n = i = 1 ∑ n c i λ i k x i
不妨令λ 1 = 1 \lambda_1=1 λ 1 = 1 ∣ λ i ∣ ≤ 1 |\lambda_i|\leq 1 ∣ λ i ∣ ≤ 1 u ∞ = lim k → ∞ A k u 0 = lim k → ∞ ∑ i = 1 k c i λ i k x i = c 1 x 1 \bm{u_\infty}=\lim_{k\to\infty}{A^k\bm{u_0}}=\lim_{k\to\infty}{\sum_{i=1}^k{c_i\lambda_i^k\bm{x_i}}}=c_1\bm{x_1} u ∞ = k → ∞ lim A k u 0 = k → ∞ lim i = 1 ∑ k c i λ i k x i = c 1 x 1
因为u ∞ u_\infty u ∞ c 1 = 1 c_1=1 c 1 = 1 u ∞ = x 1 \bm{u_\infty}=\bm{x_1} u ∞ = x 1
值得注意的是,除包含 λ = 1 \lambda=1 λ = 1 λ = − 1 \lambda=-1 λ = − 1 λ 1 = 1 \lambda_1=1 λ 1 = 1 λ 2 = − 1 \lambda_2=-1 λ 2 = − 1 u ∞ = lim k → ∞ ∑ i = 1 k c i λ i k x i = c 1 x 1 + ( − 1 ) k c 2 x 2 \bm{u_\infty}=\lim_{k\to\infty}{\sum_{i=1}^k{c_i\lambda_i^k\bm{x_i}}}=c_1\bm{x_1}+(-1)^k c_2\bm{x_2} u ∞ = k → ∞ lim i = 1 ∑ k c i λ i k x i = c 1 x 1 + ( − 1 ) k c 2 x 2
得u ∞ = x 1 + ( − 1 ) k x 2 \bm{u_\infty}=\bm{x_1}+(-1)^k\bm{x_2} u ∞ = x 1 + ( − 1 ) k x 2 k k k
如:A = [ 0 1 1 0 ] A=\begin{bmatrix}0&1\\1&0\\\end{bmatrix} A = [ 0 1 1 0 ] λ 1 = 1 , λ 2 = − 1 \lambda_1=1,\lambda_2=-1 λ 1 = 1 , λ 2 = − 1
也可以参考第 21 章 PageRank 算法
规划论又称数学规划,运筹学(Operations research )的一个分支。 规划论是指在既定条件(约束条件)下,按照某一衡量指标(目标函数)在多种 方案中寻求最优方案(取最大或最小值)。规划论包括线性规划、非线性规划和动态规划等,是一种优化算法或方法(Optimization algorithms and methods )
数学优化(Mathematical optimization )
优化技术 :
线性规划 :
当目标函数与约束条件都是线形的,则称为线性规划(Linear programming )。
求解方法:图解法(graphical method)、单纯形法(simplex algorithm )、对偶单纯形法等
非线性规划 :
除去线性规划,则为非线性规划(Nonlinear programming )。其中,凸规划(前面的章节有讲到凸优化)、二次规划(Quadratic programming )、几何规划都是一种特殊的非线性规划。
求解方法:拉格朗日乘子法、可行方向法、制约函数法(constrained function method )等。
内点法(Interior point methods )是一种求解线性规划或非线性凸优化问题的算法。
无约束优化问题 :
去除带约束的规划问题,则为无约束优化问题(Unconstrained convex optimization,对应的有约束优化(Constrained optimization ))。
求解方法: 1、 最速下降法(也叫梯度下降) 2、 共轭梯度下降 3、 牛顿法 4、 拟牛顿法
动态规划 :
若规划问题与时间有关,则称为动态规划(Dynamic programming );
把多阶段过程转化为一系列单阶段问题,逐个求解,解决这类问题的方法称为动态规划,它是一种方法、考察问题的一种途径,但不是一种特殊的算法。 没有统一的标准模型,也没有构造模型的通用方法,甚至还没有判断一个问题能否构造动态规划模型的准则。这样就只能对每类问题进行具体分析,构造具体的模型。对于较复杂的问题在选择状态、决策、确定状态转移规律等方面需要丰富的想象力和灵活的技巧性,这就带来了应用上的局限性。
动态规划一般可分为线性动规,区域动规,树形动规,背包动规(Knapsack problem )四类。
随机规划 :
若规划问题与随机变量有关,则称为随机规划(Stochastic programming )。
随机动态规划 :
Stochastic dynamic programming
组合规划 :
若规划问题与有限个事物的排列组合有关,则称为组合规划(combinatorial optimization )
[10-1] Rabiner L,Juang B. An introduction to hidden markov Models . IEEE ASSPMagazine,January 1986
[10-2] Rabiner L. A tutorial on hidden Markov models and selected applications in speechrecognition . Proceedings of IEEE,1989
[10-3] Baum L,et al. A maximization technique occuring in the statistical analysis of probabilistic functions of Markov chains . Annals of Mathematical Statistics,1970,41: 164–171
[10-4] Bilmes JA. A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models .
[10-5] Lari K,Young SJ. Applications of stochastic context-free grammars using the Inside-Outside algorithm,Computer Speech & Language,1991,5(3): 237–257
[10-6] Ghahramani Z. Learning Dynamic Bayesian Networks . Lecture Notes in ComputerScience,Vol. 1387,1997,168–197
以下来自隐马尔可夫模型
[10-7] J. Li, A. Najmi, R. M. Gray, Image classification by a two dimensional hidden Markov model,IEEE Transactions on Signal Processing , 48(2):517-33, February 2000. [2-D HMM] (download )
[10-8] J. Li, R. M. Gray, R. A. Olshen, Multiresolution image classification by hierarchical modeling with two dimensional hidden Markov models, IEEE Transactions on Information Theory , 46(5):1826-41, August 2000. [2-D MHMM] (download )
[10-9] J. Li, W. Miller, Significance of inter-species matches when evolutionary rate varies, Journal of Computational Biology , 10(3-4):537-554, 2003. [HMMMO] (download )
[10-10] J. Li, J. Z. Wang, Studying digital imagery of ancient paintings by mixtures of stochastic models, IEEE Transactions on Image Processing, 12(3):340-353, 2004. [Mixture of 2-D MHMMs] (download )
条件随机场 (Conditional random field, CRF )条件随机场(CRFs)是一类常用的统计建模方法(statistical modeling methods ),常用于模式识别(pattern recognition )和机器学习,并用于结构预测(structured prediction )。
相关的机器学习库有PyStruct 和python-crfsuite
这里推荐学习:机器学习-白板推导系列(十七)-条件随机场CRF(Conditional Random Field) 以及论文Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data
条件随机场是在无向图上的判别模型。
条件随机场是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型,其特点是假设输出随机变量构成马尔可夫随机场。
条件随机场 (conditional random field)是给定随机变量X条件下,随机变量Y的马尔可夫随机场。X X X Y Y Y P ( Y ∣ X ) P(Y|X) P ( Y ∣ X ) Y Y Y Y Y Y G = ( V , E ) G=(V,E) G = ( V , E ) p ( Y v ∣ X , Y w , w ≠ v ) = p ( Y v ∣ X , Y w , w ∼ v ) p(\boldsymbol{Y}_v |\boldsymbol{X}, \boldsymbol{Y}_w, w \neq v) = p(\boldsymbol{Y}_v |\boldsymbol{X}, \boldsymbol{Y}_w, w \sim v) p ( Y v ∣ X , Y w , w = v ) = p ( Y v ∣ X , Y w , w ∼ v ) v v v P ( Y ∣ X ) P(Y|X) P ( Y ∣ X ) w ∼ v w \sim v w ∼ v G = ( V , E ) G=(V,E) G = ( V , E ) v v v w w w w ≠ v w \neq v w = v v v v Y v Y_v Y v Y u Y_u Y u Y w Y_w Y w v v v u u u w w w
线性链条件随机场 (linear chain conditional random field)假设X和Y有相同的图结构。
条件随机场在定义中并没有要求X和Y具有相同的结构。现实中,一般假设X和Y有相同的图结构。
设X = ( X 1 , X 2 , . . . , X n ) , Y = ( Y 1 , Y 2 , . . . , Y n ) X=(X_1,X_2,...,X_n),Y=(Y_1,Y_2,...,Y_n) X = ( X 1 , X 2 , ... , X n ) , Y = ( Y 1 , Y 2 , ... , Y n ) X X X Y Y Y P ( Y ∣ X ) P(Y|X) P ( Y ∣ X ) P ( Y i ∣ X , Y 1 , . . . , Y i − 1 , Y i + 1 , . . . , Y n ) = P ( Y i ∣ X , Y i − 1 , Y i + 1 ) i = 1 , 2 , . . . , n ( 当 i = 1 和 n 时只考虑单边 ) P(Y_i|X,Y_1,...,Y_{i-1},Y_{i+1},...,Y_n) = P(Y_i|X,Y_{i-1},Y_{i+1})\\ i=1,2,...,n(当i=1和n时只考虑单边) P ( Y i ∣ X , Y 1 , ... , Y i − 1 , Y i + 1 , ... , Y n ) = P ( Y i ∣ X , Y i − 1 , Y i + 1 ) i = 1 , 2 , ... , n ( 当 i = 1 和 n 时只考虑单边 ) P ( Y ∣ X ) P(Y|X) P ( Y ∣ X )
graph LR
Y1(("Y₁"))
Y2(("Y₂"))
Yi(("Yᵢ"))
Yn(("Yₙ"))
Xg(("X₁:ₙ"))
Y1---Y2-.-Yi-.-Yn
Y1---Xg
Y2---Xg
Yi---Xg
Xg---Yn
style Y1 fill:#fff
style Y2 fill:#fff
style Yi fill:#fff
style Yn fill:#fff
style Xg fill:#f96
线性链条件随机场可以用于标注等问题。X X X Y Y Y
这时,在条件概率模型P(Y|X)中,Y是输出变量,表示标记序列,X是输入变量,表示需要标注的观测序列。也把标记序列称为状态序列。P ^ ( Y ∣ X ) \hat{P}(Y|X) P ^ ( Y ∣ X ) P ^ ( Y ∣ X ) \hat{P}(Y|X) P ^ ( Y ∣ X ) y ^ \hat{y} y ^
根据无向图的因子分解 ,得:P ( Y ∣ X ) = 1 Z e x p ∑ i = 1 K F i ( x c i ) P(Y|X) = \frac{1}{Z} exp\sum_{i=1}^K F_i(x_{ci}) P ( Y ∣ X ) = Z 1 e x p i = 1 ∑ K F i ( x c i ) y t − 1 , y t , x 1 : T y_{t-1},y_t,x_{1:T} y t − 1 , y t , x 1 : T P ( Y ∣ X ) = 1 Z e x p ∑ t = 1 T F ( y t − 1 , y t , x 1 : T ) P(Y|X) = \frac{1}{Z} exp\sum_{t=1}^T F(y_{t-1},y_t,x_{1:T}) P ( Y ∣ X ) = Z 1 e x p t = 1 ∑ T F ( y t − 1 , y t , x 1 : T ) F ( y t − 1 , y t , x 1 : T ) F(y_{t-1},y_t,x_{1:T}) F ( y t − 1 , y t , x 1 : T ) x 1 : T x_{1:T} x 1 : T y t y_t y t y t − 1 , y t y_{t-1},y_t y t − 1 , y t F ( y t − 1 , y t , x 1 : T ) = △ y t , x 1 : T + △ y t − 1 , y t , x 1 : T F(y_{t-1},y_t,x_{1:T})=\triangle y_{t},x_{1:T} + \triangle y_{t-1},y_{t},x_{1:T} F ( y t − 1 , y t , x 1 : T ) = △ y t , x 1 : T + △ y t − 1 , y t , x 1 : T △ y t − 1 , x 1 : T \triangle y_{t-1},x_{1:T} △ y t − 1 , x 1 : T △ y t , x 1 : T \triangle y_t,x_{1:T} △ y t , x 1 : T 状态函数 ,即表示为在t t t y t y_t y t △ y t − 1 , y t , x 1 : T \triangle y_{t-1},y_t,x_{1:T} △ y t − 1 , y t , x 1 : T 转移函数 ,即表示当前节点y t y_t y t y t − 1 y_{t-1} y t − 1 局部特征函数 t k t_k t k △ y t − 1 , y t , x 1 : T = ∑ k = 1 K λ k t k ( y i − 1 , y i , X , i ) , k = 1 , 2 , . . , K \triangle y_{t-1},y_t,x_{1:T} =\sum_{k=1}^K \lambda_k t_k(y_{i-1},y_i,X,i),k=1,2,..,K △ y t − 1 , y t , x 1 : T = k = 1 ∑ K λ k t k ( y i − 1 , y i , X , i ) , k = 1 , 2 , .. , K K K K i i i λ k \lambda_k λ k 节点特征函数 ,这类特征函数只和当前节点有关,即为上面的△ y t , x 1 : T = ∑ l = 1 L μ l s l ( y i , X , i ) , l = 1 , 2 , … , L \triangle y_t,x_{1:T} =\sum_{l=1}^L \mu_l s_l(y_i,X,i),l=1,2,…,L △ y t , x 1 : T = l = 1 ∑ L μ l s l ( y i , X , i ) , l = 1 , 2 , … , L L L L i i i μ l \mu_l μ l t k { y t − 1 = 名词 , y t = 动词 , x 1 : T } = 1 t k { y t − 1 = 名词 , y t = 助词 , x 1 : T } = 0 t_k\{y_{t-1}=名词, y_t=动词, x_{1:T}\} = 1 \\ t_k\{y_{t-1}=名词, y_t=助词, x_{1:T}\} = 0 t k { y t − 1 = 名词 , y t = 动词 , x 1 : T } = 1 t k { y t − 1 = 名词 , y t = 助词 , x 1 : T } = 0 P ( Y ∣ X ) = 1 Z ( X ) e x p ∑ i = 1 T ( ∑ k = 1 K λ k t k ( y i − 1 , y i , X , i ) + ∑ l = 1 L μ l s l ( y i , X , i ) ) P(Y|X)=\frac{1}{Z(X)}exp \sum_{i=1}^ T \bigg (\sum_{k=1}^K \lambda_k t_k (y_{i-1},y_i,X,i) +\sum_{l=1}^L \mu_l s_l (y_i,X,i)\bigg ) P ( Y ∣ X ) = Z ( X ) 1 e x p i = 1 ∑ T ( k = 1 ∑ K λ k t k ( y i − 1 , y i , X , i ) + l = 1 ∑ L μ l s l ( y i , X , i ) ) Y Y Y T T T X = x 1 : T X = x_{1:T} X = x 1 : T T T T Z ( X ) Z(X) Z ( X ) Z ( X ) = ∑ Y e x p ∑ i = 1 T ( ∑ k = 1 K λ k t k ( y i − 1 , y i , X , i ) + ∑ l L μ l s l ( y i , X , i ) ) Z(X)=\sum_Y exp \sum_{i=1}^T \bigg(\sum_{k=1}^K\lambda_k t_k (y_{i-1},y_i,X,i) +\sum_{l}^L\mu_l s_l (y_i,X,i)\bigg) Z ( X ) = Y ∑ e x p i = 1 ∑ T ( k = 1 ∑ K λ k t k ( y i − 1 , y i , X , i ) + l ∑ L μ l s l ( y i , X , i ) ) 模型的简化表示-数值表示 K = K 1 + K 2 K=K_1+K_2 K = K 1 + K 2 K 1 K_1 K 1 t k t_k t k K 2 K_2 K 2 s l s_l s l f k ( y i − 1 , y i , X , i ) f_k(y_{i-1},y_i,X,i) f k ( y i − 1 , y i , X , i ) f k ( y i − 1 , y i , X , i ) = { t k ( y i − 1 , y i , X , i ) k = 1 , 2 , . . , K 1 s l ( y i , X , i ) k = K 1 + l , l = 1 , 2 , … , K 2 \begin{aligned}f_k(y_{i-1},y_i,X,i)=\left\{\begin{aligned} & t_k (y_{i-1},y_i,X,i) \qquad k = 1,2,..,K_1 \\ & s_l (y_i,X,i) \qquad k = K_1+l,l=1,2,…,K_2 \end{aligned}\right.\end{aligned} f k ( y i − 1 , y i , X , i ) = { t k ( y i − 1 , y i , X , i ) k = 1 , 2 , .. , K 1 s l ( y i , X , i ) k = K 1 + l , l = 1 , 2 , … , K 2 f k ( y i − 1 , y i , X , i ) f_k(y_{i-1},y_i,X,i) f k ( y i − 1 , y i , X , i ) f k ( Y , X ) = ∑ i = 1 T f k ( y i − 1 , y i , X , i ) \begin{aligned}f_k(Y,X)=\sum_{i=1}^T f_k(y_{i-1},y_i,X,i)\end{aligned} f k ( Y , X ) = i = 1 ∑ T f k ( y i − 1 , y i , X , i ) f k ( y i − 1 , y i , x , i ) f_k(y_{i-1},y_i,x,i) f k ( y i − 1 , y i , x , i ) w k w_k w k w k = { λ k k = 1 , 2 , . . , K 1 μ l k = K 1 + l , l = 1 , 2 , … , K 2 \begin{aligned}w_k=\left\{ \begin{aligned} & \lambda_k \qquad k = 1,2,..,K_1 \\ & \mu_l \qquad k = K_1+l,l=1,2,…,K_2 \end{aligned}\right.\end{aligned} w k = { λ k k = 1 , 2 , .. , K 1 μ l k = K 1 + l , l = 1 , 2 , … , K 2 P ( Y ∣ X ) = 1 Z ( X ) e x p ∑ k = 1 K w k f k ( Y , X ) \begin{aligned}P(Y|X)=\frac{1}{Z(X)}exp\sum_{k=1}^K w_kf_k(Y,X)\end{aligned} P ( Y ∣ X ) = Z ( X ) 1 e x p k = 1 ∑ K w k f k ( Y , X ) Z ( X ) = ∑ Y e x p ∑ k = 1 K w k f k ( Y , X ) \begin{aligned}Z(X)=\sum_Y exp\sum_{k=1}^Kw_kf_k(Y,X)\end{aligned} Z ( X ) = Y ∑ e x p k = 1 ∑ K w k f k ( Y , X ) 模型的简化表示-向量表示 f k ( Y , X ) f_k(Y,X) f k ( Y , X ) w k w_k w k F ( Y , X ) F(Y,X) F ( Y , X ) W W W K × 1 K \times 1 K × 1 W = [ w 1 w 2 … w K ] \begin{aligned}W =\left [ \begin{aligned} w_1\\ w_2\\ …\\ w_K \end{aligned}\right]\end{aligned} W = ⎣ ⎡ w 1 w 2 … w K ⎦ ⎤ F ( Y , X ) = [ f 1 ( Y , X ) f 2 ( Y , X ) … … … f K ( Y , X ) ] \begin{aligned}F(Y,X) =\left[ \begin{aligned} f_1(Y,X)\\ f_2(Y,X)\\ ………\\ f_K(Y,X) \end{aligned}\right]\end{aligned} F ( Y , X ) = ⎣ ⎡ f 1 ( Y , X ) f 2 ( Y , X ) ……… f K ( Y , X ) ⎦ ⎤ P W ( Y ∣ X ) = e x p ( W ∙ F ( Y , X ) ) Z ( X , W ) = e x p ( W ∙ F ( Y , X ) ) ∑ Y e x p ( W ∙ F ( Y , X ) ) \begin{aligned}P_W(Y|X) = \frac{exp(W \bullet F(Y,X))}{Z(X,W)}\\ = \frac{exp(W \bullet F(Y,X))}{\sum_Y exp(W \bullet F(Y,X))}\end{aligned} P W ( Y ∣ X ) = Z ( X , W ) e x p ( W ∙ F ( Y , X )) = ∑ Y e x p ( W ∙ F ( Y , X )) e x p ( W ∙ F ( Y , X )) 要解决的三个问题
Inference(概率计算问题):计算条件概率分布,即给定X序列,算出序列中每个位置所对应标注的概率,即:P ( y t ∣ X ) P(y_t|X) P ( y t ∣ X )
Learning:把参数学习出来(parameter estimation),也就是给定N N N W W W W ^ = a r g m a x ∏ i = 1 N P ( Y ( i ) ∣ X ( i ) ) \hat{W}=argmax\prod_{i=1}^N P(Y^{(i)}|X^{(i)}) W ^ = a r g ma x ∏ i = 1 N P ( Y ( i ) ∣ X ( i ) )
Decoding:给定X序列,找到一个最有可能的标注序列,即:Y ^ = a r g m a x P ( Y ∣ X ) \hat{Y}=argmax P(Y|X) Y ^ = a r g ma x P ( Y ∣ X ) Y = y 1 y 2 . . y T Y=y_1y_2..y_T Y = y 1 y 2 .. y T
Inference:条件概率(前向-后向) Learning(参数估计) Decoding(Vitebi)
模型 :P W ( Y ∣ X ) = e x p ( W ∙ F ( Y , X ) ) Z ( X , W ) = e x p ( W ∙ F ( Y , X ) ) ∑ Y e x p ( W ∙ F ( Y , X ) ) \begin{aligned}P_W(Y|X) = \frac{exp(W \bullet F(Y,X))}{Z(X,W)}\\ = \frac{exp(W \bullet F(Y,X))}{\sum_Y exp(W \bullet F(Y,X))}\end{aligned} P W ( Y ∣ X ) = Z ( X , W ) e x p ( W ∙ F ( Y , X )) = ∑ Y e x p ( W ∙ F ( Y , X )) e x p ( W ∙ F ( Y , X )) 策略 :W ^ = arg max W ∏ i = 1 N P ( Y ( i ) ∣ X ( i ) ) \hat{W}=\mathop{\arg\max}\limits_{W} \prod_{i=1}^N P(Y^{(i)}|X^{(i)}) W ^ = W arg max i = 1 ∏ N P ( Y ( i ) ∣ X ( i ) ) 算法 :
参考【NLP】从隐马尔科夫到条件随机场 以及视频机器学习-白板推导系列(十七)-条件随机场CRF(Conditional Random Field)
随机场 (Random field, RF )是由若干个位置组成的整体,当给每一个位置中按照某种分布(或者是某种概率)随机赋予一个值之后,其全体就叫做随机场。
以词性标注为例:
假如我们有10个词形成的句子需要做词性标注。这10个词每个词的词性可以在我们已知的词性集合(名词,动词…)中去选择。当我们为每个词选择完词性后,这就形成了一个随机场。
马尔科夫随机场 (Markov random field, MRF )是随机场的特例,它假设随机场中某一个位置的赋值仅仅与和它相邻的位置的赋值有关,和与其不相邻的位置的赋值无关。
条件随机场 (CRF)是马尔科夫随机场的特例,它假设马尔科夫随机场中只有𝑋和𝑌两种变量,𝑋一般是给定的,而𝑌一般是在给定𝑋的条件下我们的输出。这样马尔科夫随机场就特化成了条件随机场。
在我们10个词的句子词性标注的例子中,𝑋是词,𝑌是词性。因此,如果我们假设它是一个马尔科夫随机场,那么它也就是一个CRF。
线性链条件随机场 (Linear-CRF)X = ( x 1 , x 2 , … , x T ) , Y = ( y 1 , y 2 , … , y T ) X=(x_1,x_2,…,x_T),Y=(y_1,y_2,…,y_T) X = ( x 1 , x 2 , … , x T ) , Y = ( y 1 , y 2 , … , y T )
判别模型Maximum Entropy Markov Models for Information Extraction and Segmentation Maximum Entropy Markov Models Hidden Markov Model and Naive Bayes relationship Maximum Entropy Markov Models and Logistic Regression
Maximum-Entropy Markov Model
介绍概率图模型(Probabilistic Graphical Model)之前,先简单了解下结构学习 (Structured Learning ),相比于回归,输出一个标量或者预测,输出一个向量,结构化学习的输出更加复杂,可以是图像,可以是语句,可以是树结构,等。参见
什么是结构化学习?What is structured learning?
概率图模型 (Probabilistic Graphical Model,PGM ),简称图模型(Graphical Model,GM),是指一种用图结构来描述多元随机变量之间条件独立关系的概率模型,从而给研究高维空间中的概率模型带来了很大的便捷性。
图模型有三个基本问题 :
表示(Representation)问题:对于一个概率模型,如何通过图结构来描述变量之间的依
学习(Learning)问题:图模型的学习包括图结构的学习和参数的学习.在本章中,
推断(Inference)问题:在已知部分变量时,计算其他变量的条件概率分布
{ R e p r e s e n t a t i o n ( 表示 ) { 有向图 Bayesian Network 无向图 Markov Network L e a r n i n g ( 学习 ) { 参数学习 { 完备数据 隐变量 → E M 结构学习 I n f e r e n c e ( 推断 ) { 精确推断 近似推断 { 确定性近似 → 变分推断 随机近似 → M C M C \begin{cases}
Representation(表示) & \begin{cases} \text{有向图 Bayesian Network} \\ \text{无向图 Markov Network} \end{cases} \\
Learning(学习) & \begin{cases} \text{参数学习} & \begin{cases} \text{完备数据} \\ \text{隐变量} \to EM \end{cases} \\ \text{结构学习} \end{cases}\\
Inference(推断) & \begin{cases} \text{精确推断} \\ \text{近似推断} & \begin{cases} \text{确定性近似} \to 变分推断 \\ \text{随机近似} \to MCMC \end{cases} \end{cases} \\
\end{cases} ⎩ ⎨ ⎧ R e p rese n t a t i o n ( 表示 ) L e a r nin g ( 学习 ) I n f ere n ce ( 推断 ) { 有向图 Bayesian Network 无向图 Markov Network ⎩ ⎨ ⎧ 参数学习 结构学习 { 完备数据 隐变量 → EM ⎩ ⎨ ⎧ 精确推断 近似推断 { 确定性近似 → 变分推断 随机近似 → MCMC
图的表示 :G = ( V , E ) G=(V,E) G = ( V , E ) V V V E ⊆ { ( x , y ) ∣ ( x , y ) ∈ V 2 and x ≠ y } {\displaystyle E\subseteq \{(x,y)\mid (x,y)\in V^{2}\;{\textrm {and}}\;x\neq y\}} E ⊆ {( x , y ) ∣ ( x , y ) ∈ V 2 and x = y }
也有些地方有向边一般用尖括号表示<>;而无向边一般用弧形括号表示();如:G 1 = ( V , E ) V ( G 1 ) = { v 1 , v 2 , v 3 } E ( G 1 ) = { ⟨ v 1 , v 2 ⟩ , ⟨ v 1 , v 3 ⟩ , ⟨ v 2 , v 3 ⟩ } G1=(V,E) \\ V(G1)=\{v1,v2,v3\}\\ E(G1)=\{\braket{v1,v2},\braket{v1,v3},\braket{v2,v3}\} G 1 = ( V , E ) V ( G 1 ) = { v 1 , v 2 , v 3 } E ( G 1 ) = { ⟨ v 1 , v 2 ⟩ , ⟨ v 1 , v 3 ⟩ , ⟨ v 2 , v 3 ⟩ }
graph LR
v1(("v1"))-->v2(("v2"))
v1-->v3(("v3"))
v2-->v3
无向图:G 2 = ( V , E ) V ( G 2 ) = { v 1 , v 2 , v 3 , v 4 } E ( G 2 ) = { ( v l , v 2 ) , ( v 1 , v 3 ) , ( v 1 , v 4 ) , ( v 2 , v 3 ) , ( v 2 , v 4 ) , ( v 3 , v 4 ) } G2=(V,E) \\ V(G2)=\{v1,v2,v3,v4\} \\ E(G2)=\{(vl,v2),(v1,v3),(v1,v4),(v2,v3),(v2,v4),(v3,v4)\} G 2 = ( V , E ) V ( G 2 ) = { v 1 , v 2 , v 3 , v 4 } E ( G 2 ) = {( v l , v 2 ) , ( v 1 , v 3 ) , ( v 1 , v 4 ) , ( v 2 , v 3 ) , ( v 2 , v 4 ) , ( v 3 , v 4 )}
graph LR
v1(("v1"))---v2(("v2"))
v1---v3(("v3"))
v1---v4(("v4"))
v2---v3
v2---v4
v3---v4
有向图模型(Directed Graphical Model)又称贝叶斯网络(Bayesian Network )或信念网络(Belief Network,BN)或(causal networks)是一类用有向图(Directed Graphical )来描述随机向量概率分布的模型.
这里是 有向无环图(DAG)
定义和概率 Definitions and concepts:
parent 父节点
概率分布的分解(Factorization definition) :X X X G G G X X X p ( X ) = ∏ v ∈ V p ( x v ∣ x pa ( v ) ) p(X)=\prod _{v\in V}p\left(x_{v}\,{\big |}\,x_{\operatorname {pa} (v)}\right) p ( X ) = v ∈ V ∏ p ( x v ∣ ∣ x pa ( v ) ) x pa ( v ) x_{\operatorname {pa} (v)} x pa ( v ) x v x_{v} x v
graph LR
x1(("x₁"))-->x2(("x₂"))-->x4(("x₄"))
x1-->x3(("x₃"))
x2-->x3
x3-->x5(("x₅"))
X = x 1 , x 2 , x 3 , x 4 , x 5 X=x_1,x_2,x_3,x_4,x_5 X = x 1 , x 2 , x 3 , x 4 , x 5 V = { x 1 , x 2 , x 3 , x 4 , x 5 } V=\{x_1,x_2,x_3,x_4,x_5\} V = { x 1 , x 2 , x 3 , x 4 , x 5 } E = { ⟨ x 1 , x 2 ⟩ , ⟨ x 1 , x 3 ⟩ , ⟨ x 2 , x 3 ⟩ , ⟨ x 2 , x 4 ⟩ } , ⟨ x 3 , x 5 ⟩ E=\{\braket{x_1,x_2},\braket{x_1,x_3},\braket{x_2,x_3},\braket{x_2,x_4}\},\braket{x_3,x_5} E = { ⟨ x 1 , x 2 ⟩ , ⟨ x 1 , x 3 ⟩ , ⟨ x 2 , x 3 ⟩ , ⟨ x 2 , x 4 ⟩ } , ⟨ x 3 , x 5 ⟩ G = ( V , E ) G=(V,E) G = ( V , E ) p ( X ) = p ( x 1 , x 2 , x 3 , x 4 , x 5 ) = p ( x 1 ) p ( x 2 ∣ x 1 ) p ( x 3 ∣ x 1 , x 2 ) p ( x 4 ∣ x 2 ) p ( x 5 ∣ x 3 ) p(X) = p(x_1,x_2,x_3,x_4,x_5) = p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)p(x_4|x_2)p(x_5|x_3) p ( X ) = p ( x 1 , x 2 , x 3 , x 4 , x 5 ) = p ( x 1 ) p ( x 2 ∣ x 1 ) p ( x 3 ∣ x 1 , x 2 ) p ( x 4 ∣ x 2 ) p ( x 5 ∣ x 3 )
因果网络(Causal networks) :t a i l → h e a d ( 因 → 果 ) tail \rightarrow head (因\rightarrow 果) t ai l → h e a d ( 因 → 果 ) 条件独立性 就比较复杂。
Pattern
Model
条件独立性
Chain(间接因果关系/tail to head)
X → Y → Z X\rightarrow Y\rightarrow Z X → Y → Z 已知Y时,X和Z为条件独立,即 X ⊥ ⊥ Z ∣ Y X \perp \!\!\!\perp Z\mid Y X ⊥ ⊥ Z ∣ Y
Fork(共因关系/tail to tail)
X ← Y → Z X\leftarrow Y\rightarrow Z X ← Y → Z 已知Y时,X和Z为条件独立,即 X ⊥ ⊥ Z ∣ Y X \perp \!\!\!\perp Z \mid Y X ⊥ ⊥ Z ∣ Y
Collider(共果关系/head to head)
X → Y ← Z X\rightarrow Y\leftarrow Z X → Y ← Z 已知Y时,X和Z为不独立,即 X ⊥ ⊥ / Z ∣ Y X \perp \!\!\!\perp \!\!\!\!\!\!/ \;\; Z \mid Y X ⊥ ⊥ / Z ∣ Y
局部马尔可夫性质(Local Markov property) :X v ⊥ ⊥ X V ∖ de ( v ) ∣ X pa ( v ) for all v ∈ V {\displaystyle X_{v}\perp \!\!\!\perp X_{V\,\smallsetminus \,\operatorname {de} (v)}\mid X_{\operatorname {pa} (v)}\quad {\text{for all }}v\in V} X v ⊥ ⊥ X V ∖ de ( v ) ∣ X pa ( v ) for all v ∈ V X V ∖ de ( v ) X_{V\,\smallsetminus \,\operatorname {de} (v)} X V ∖ de ( v )
马尔可夫毯 (Markov blanket ):X ∈ U X\in U X ∈ U M B ⊂ U ( X ∉ M B ) MB\subset U(X\notin MB) MB ⊂ U ( X ∈ / MB ) X ⊥ ⊥ { U − M B − { X } } ∣ M B X\perp \!\!\!\perp\{U-MB-\{X\}\}|MB X ⊥ ⊥ { U − MB − { X }} ∣ MB M B MB MB X X X
D划分(d-separation) :
如果p是这样的路径 u ⋯ ← m ← ⋯ v {\displaystyle u\cdots \leftarrow m\leftarrow \cdots v} u ⋯ ← m ← ⋯ v u ⋯ → m → ⋯ v {\displaystyle u\cdots \rightarrow m\rightarrow \cdots v} u ⋯ → m → ⋯ v m ∈ Z m \in Z m ∈ Z
如果p是这样的路径 u ⋯ ← m → ⋯ v {\displaystyle u\cdots \leftarrow m\rightarrow \cdots v} u ⋯ ← m → ⋯ v m ∈ Z m \in Z m ∈ Z
如果p是这样的路径 u ⋯ → m ← ⋯ v {\displaystyle u\cdots \rightarrow m\leftarrow \cdots v} u ⋯ → m ← ⋯ v m ∉ Z m \notin Z m ∈ / Z X u ⊥ ⊥ X v ∣ X Z X_{u}\perp \!\!\!\perp X_{v}\mid X_{Z} X u ⊥ ⊥ X v ∣ X Z
常见的有向图模型 :
graph TD
y(("y"))
y-->x1(("x₁"))
y-->x2(("x₂"))
y-->x3(("x₃"))
style y fill:#fff
style x1 fill:#f96
style x2 fill:#f96
style x3 fill:#f96
由图可得P ( y , x 1 , x 2 , x 3 ) = P ( y ) P ( x 1 ∣ y ) P ( x 2 ∣ y ) P ( x 3 ∣ y ) = P ( x 1 , x 2 , x 3 ∣ y ) P ( y ) ⇓ P ( x 1 , x 2 , x 3 ∣ y ) = P ( x 1 ∣ y ) P ( x 2 ∣ y ) P ( x 3 ∣ y ) P(y,x_1,x_2,x_3) = P(y)P(x_1|y)P(x_2|y)P(x_3|y) = P(x_1,x_2,x_3|y)P(y) \\ \Darr\\ P(x_1,x_2,x_3|y)=P(x_1|y)P(x_2|y)P(x_3|y) P ( y , x 1 , x 2 , x 3 ) = P ( y ) P ( x 1 ∣ y ) P ( x 2 ∣ y ) P ( x 3 ∣ y ) = P ( x 1 , x 2 , x 3 ∣ y ) P ( y ) ⇓ P ( x 1 , x 2 , x 3 ∣ y ) = P ( x 1 ∣ y ) P ( x 2 ∣ y ) P ( x 3 ∣ y ) P ( X ∣ y ) = ∏ i = 1 n P ( x i ∣ y ) P(X|y) = \prod_{i=1}^n P(x_i|y) P ( X ∣ y ) = ∏ i = 1 n P ( x i ∣ y )
graph LR
y1(("y₁"))
y1-->x1(("x₁"))
y1-->y2(("y₂"))
y2-->x2(("x₂"))
y2-->y3(("y₃"))
y3-->x3(("x₃"))
y3-->y4(("y₄"))
y4-->x4(("x₄"))
style y1 fill:#fff
style y2 fill:#fff
style y3 fill:#fff
style y4 fill:#fff
style x1 fill:#f96
style x2 fill:#f96
style x3 fill:#f96
style x4 fill:#f96
我们能从图中直接得到P ( y t ∣ y t − 1 , . . . , y 1 , x t − 1 , . . . , x 1 ) = P ( y t ∣ y t − 1 ) P(y_t|y_{t-1},...,y_1,x_{t-1},...,x_1) = P(y_t|y_{t-1}) P ( y t ∣ y t − 1 , ... , y 1 , x t − 1 , ... , x 1 ) = P ( y t ∣ y t − 1 ) P ( x t ∣ x T , . . . , x t + 1 , x t − 1 , . . . , x 1 , Y ) = P ( x t ∣ y t ) P(x_t|x_{T},...,x_{t+1},x_{t-1},...,x_1,Y) = P(x_t|y_{t}) P ( x t ∣ x T , ... , x t + 1 , x t − 1 , ... , x 1 , Y ) = P ( x t ∣ y t )
无向图模型(Undirected Graphical Model)又称马尔可夫随机场(Markov random field, MRF )或马尔可夫网络(Markov network)是一类用无向图(Undirected Graphical )来描述一组具有局部马尔可夫性质的随机向量𝑿的联合概率分布的模型.Global Markov ⟺ Local Markov ⟺ Pair Markov ⇔ H a m m e s l e y − C l i f f o r d 因子分解 \text{Global Markov} \iff \text{Local Markov}\iff\text{Pair Markov}\xLeftrightarrow{Hammesley−Clifford } 因子分解 Global Markov ⟺ Local Markov ⟺ Pair Markov H amm es l ey − Cl i ff or d 因子分解
团分解,因子分解 (Clique factorization):团 (clique)。若C是无向图G的一个团,并且不能再加进任何一个G的结点使其成为一个更大的团,则称此C为最大团 (maximal clique)。X = ( X v ) v ∈ V {\displaystyle X=(X_{v})_{v\in V}} X = ( X v ) v ∈ V X C X_C X C P ( X ) P(X) P ( X ) ϕ C ( x C ) \phi_C (x_C) ϕ C ( x C ) P ( X ) = 1 Z ∏ C ∈ cl ( G ) ϕ C ( X C ) P(X) =\frac{1}{Z} \prod_{C \in \operatorname{cl}(G)} \phi_C (X_C) P ( X ) = Z 1 C ∈ cl ( G ) ∏ ϕ C ( X C ) Z = ∑ X ∏ C ∈ cl ( G ) ϕ C ( X C ) Z=\sum_{X}\prod_{C \in \operatorname{cl}(G)} \phi_C (X_C) Z = X ∑ C ∈ cl ( G ) ∏ ϕ C ( X C ) ϕ C ( X C ) \phi_C (X_C) ϕ C ( X C ) ϕ C ( X C ) = exp { − E ( X C ) } \phi_C (X_C) = \exp\{-E(X_C)\} ϕ C ( X C ) = exp { − E ( X C )} P ( x ) = 1 Z ∏ i = 1 K ϕ ( x C i ) = 1 Z ∏ i = 1 K exp { − E ( x C i ) } = 1 Z exp { − ∑ i = 1 K E ( x C i ) } = 1 Z exp ∑ i = 1 K F i ( x c i ) , x ∈ R p P(x) = \frac{1}{Z} \prod_{i=1}^K \phi (x_{C_{i}}) = \frac{1}{Z} \prod_{i=1}^K \exp\{-E(x_{C_{i}})\} = \frac{1}{Z}\exp\{-\sum_{i=1}^K E(x_{C_{i}})\} = \frac{1}{Z}\exp\sum_{i=1}^K F_i(x_{ci}),x \in \mathbb{R}^{p} P ( x ) = Z 1 i = 1 ∏ K ϕ ( x C i ) = Z 1 i = 1 ∏ K exp { − E ( x C i )} = Z 1 exp { − i = 1 ∑ K E ( x C i )} = Z 1 exp i = 1 ∑ K F i ( x c i ) , x ∈ R p x ∈ R p x \in \mathbb{R}^p x ∈ R p p p p ϕ \phi ϕ E E E K K K C i C_i C i i i i p ( x ∣ η ) = h ( x ) exp ( η T ⋅ T ( x ) − A ( η ) ) = h ( x ) 1 Z ( η ) exp { η T ⋅ T ( x ) } {\displaystyle p(x\mid {\boldsymbol {\eta }})=h(x)\,\exp {\Big (}{\boldsymbol {\eta^T }}\cdot \mathbf {T} (x)-A({\boldsymbol {\eta }}){\Big )}} = h(x) \frac{1}{Z(\eta)}\exp\{\eta^T \cdot \mathbf {T} (x)\} p ( x ∣ η ) = h ( x ) exp ( η T ⋅ T ( x ) − A ( η ) ) = h ( x ) Z ( η ) 1 exp { η T ⋅ T ( x )}
成对马尔可夫性 (Pairwise Markov property):X u ⊥ ⊥ X v ∣ X V ∖ { u , v } {\displaystyle X_{u}\perp \!\!\!\perp X_{v}\mid X_{V\setminus \{u,v\}}} X u ⊥ ⊥ X v ∣ X V ∖ { u , v }
局部马尔可夫性 (Local Markov property):X v ⊥ ⊥ X V ∖ N [ v ] ∣ X N ( v ) {\displaystyle X_{v}\perp \!\!\!\perp X_{V\setminus \operatorname {N} [v]}\mid X_{\operatorname {N} (v)}} X v ⊥ ⊥ X V ∖ N [ v ] ∣ X N ( v ) N ( v ) \operatorname {N} (v) N ( v ) N [ v ] = v ∪ N ( v ) {\displaystyle \operatorname {N} [v]=v\cup \operatorname {N} (v)} N [ v ] = v ∪ N ( v )
全局马尔可夫性 (Global Markov property):X A ⊥ ⊥ X B ∣ X S X_A \perp\!\!\!\perp X_B \mid X_S X A ⊥ ⊥ X B ∣ X S
道德图 (Moral graph):Moral graph )。P ( X ) = p ( x 1 ) p ( x 2 ) p ( x 3 ) p ( x 4 ∣ x 1 , x 2 , x 3 ) P(X) = p(x_1)p(x_2)p(x_3)p(x_4|x_1,x_2,x_3) P ( X ) = p ( x 1 ) p ( x 2 ) p ( x 3 ) p ( x 4 ∣ x 1 , x 2 , x 3 ) p ( x 4 ∣ x 1 , x 2 , x 3 ) p(x_4|x_1,x_2,x_3) p ( x 4 ∣ x 1 , x 2 , x 3 )
graph TD
x1(("x₁"))
x2(("x₂"))
x3(("x₃"))
x4(("x₄"))
x1-->x4
x2-->x4
x3-->x4
y1(("x₁"))
y2(("x₂"))
y3(("x₃"))
y4(("x₄"))
y1---y2
y1---y3
y1---y4
y2---y3
y2---y4
y3---y4
道德化的过程中,原有的一些条件独立性会丢失。
以上内容只是讲到了概率图的表示。
[11-1] Bishop M. Pattern Recognition and Machine Learning. Springer-Verlag,2006
[11-2] Koller D,Friedman N. Probabilistic Graphical Models: Principles and Techniques.MIT Press,2009
[11-3] Lafferty J,McCallum A,Pereira F. Conditional random fields: probabilistic models for segmenting and labeling sequence data. In: International Conference on Machine Learning,2001
[11-4] Sha F,Pereira F. Shallow parsing with conditional random fields. In: Proceedings ofthe 2003 Conference of the North American Chapter of Association for ComputationalLinguistics on Human Language Technology,Vol.1,2003
[11-5] McCallum A,Freitag D,Pereira F. Maximum entropy Markov models for informationextraction and segmentation. In: Proc of the International Conference on Machine Learning,2000
[11-6] Taskar B,Guestrin C,Koller D. Max-margin Markov networks. In: Proc of the NIPS2003,2003
[11-7] Tsochantaridis I,Hofmann T,Joachims T. Support vector machine learning forinterdependent and structured output spaces. In: ICML,2004
参考:生成模型和判别模型
分类
方法
适用问题
模型特点
模型类别
学习策略
损失函数
学习算法
监督
感知机
二分类
分离超平面
判别模型
极小化误分点到超平面距离
误分点到超平面距离
随机梯度下降
监督
k 近邻法
多分类、回归
特征空间、样本点
判别模型
—
—
—
监督
朴素贝叶斯
多分类
特征与类别的联合概率分布,条件独立假设
生成模型
极大似然估计、最大后验概率估计
对数似然损失
概率计算公式、EM 算法
监督
决策树
多分类、回归
分类树、回归树
判别模型
正则化的极大似然估计
对数似然损失
特征选择、生成、剪枝
监督
逻辑斯蒂回归
多分类
特征条件下类别的条件概率分布,对数线性模型
判别模型
极大似然估计,正则化的极大似然估计
逻辑斯蒂损失
改进的迭代尺度算法,梯度下降,拟牛顿法
监督
支持向量机
二分类
分离超平面,核技巧
判别模型
极小化正则化合页损失,软间隔最大化
合页损失
序列最小最优化算法(SMO)
监督
提升方法 (Boosting)
二分类
弱分类器的线性组合
判别模型
极小化加法模型的指数损失
指数损失
前向分布加法算法
监督
EM 算法
概率模型参数估计
含隐变量概率模型
—
极大似然估计,最大后验概率估计
对数似然损失
迭代算法
监督
隐马尔科夫模型(HMM)
标注
观测序列与状态序列的联合概率分布模型
生成模型
极大似然估计,最大后验概率估计
对数似然损失
概率计算公式,EM 算法
监督
最大熵马尔科夫模型(MEMM)
标注
-
判别模型
监督
条件随机场(CRF)
标注
状态序列条件下观测序列的条件概率分布,对数线性模型
判别模型
极大似然估计,正则化极大似然估计
对数似然损失
改进的迭代尺度算法,梯度下降,拟牛顿法
监督
马尔可夫随机场 Markov Random Fields
-
-
生成模型
模型
朴素贝叶斯法、隐马尔可夫模型是概率模型。感知机、k近邻法、支持向量机、提升方法是非概率模型。而决策树、逻辑斯谛回归与最大熵模型、条件随机场既可以看作是概率模型,又可以看作是非概率模型。
直接学习条件概率分布P(Y|X)或决策函数Y=f(X)的方法为判别方法,对应的模型是判别模型。感知机、k近邻法、决策树、逻辑斯谛回归与最大熵模型、支持向量机、提升方法、条件随机场是判别方法。首先学习联合概率分布P(X,Y),从而求得条件概率分布P(Y|X)的方法是生成方法,对应的模型是生成模型。朴素贝叶斯法、隐马尔可夫模型是生成方法。
可以用非监督学习的方法学习生成模型。具体地,应用EM算法可以学习朴素贝叶斯模型以及隐马尔可夫模型。
决策树是定义在一般的特征空间上的,可以含有连续变量或离散变量。感知机、支持向量机、k近邻法的特征空间是欧氏空间(更一般地,是希尔伯特空间)。提升方法的模型是弱分类器的线性组合,弱分类器的特征空间就是提升方法模型的特征空间。
感知机模型是线性模型,而逻辑斯谛回归与最大熵模型、条件随机场是对数线性模型。k近邻法、决策树、支持向量机(包含核函数)、提升方法使用的是非线性模型。
学习策略 [ 1 − y f ( x ) ] + log [ 1 − exp ( − y f ( x ) ) ] exp ( − y f ( x ) ) [1-yf(x)]_+ \\ \log[1-\exp(-yf(x))] \\ \exp(-yf(x)) [ 1 − y f ( x ) ] + log [ 1 − exp ( − y f ( x ))] exp ( − y f ( x )) min f ∈ H 1 N ∑ i = 1 N L ( y i , f ( x i ) ) + λ J ( f ) \min_{f \in H} \frac{1}{N}\sum_{i=1}^N L(y_i,f(x_i)) +\lambda J(f) f ∈ H min N 1 i = 1 ∑ N L ( y i , f ( x i )) + λ J ( f )
支持向量机用L2范数表示模型的复杂度。原始的逻辑斯谛回归与最大熵模型没有正则化项,可以给它们加上L2范数正则化项。提升方法没有显式的正则化项,通常通过早停止(early stopping)的方法达到正则化的效果。
以上二类分类的学习方法可以扩展到多类分类学习以及标注问题,比如标注问题的条件随机场可以看作是分类问题的最大熵模型的推广。
概率模型的学习可以形式化为极大似然估计或贝叶斯估计的极大后验概率估计。这时,学习的策略是极小化对数似然损失或极小化正则化的对数似然损失。对数似然损失可以写成− log P ( y ∣ x ) -\log P(y|x) − log P ( y ∣ x )
决策树学习的策略是正则化的极大似然估计,损失函数是对数似然损失,正则化项是决策树的复杂度。
逻辑斯谛回归与最大熵模型、条件随机场的学习策略既可以看成是极大似然估计(或正则化的极大似然估计),又可以看成是极小化逻辑斯谛损失(或正则化的逻辑斯谛损失)。
朴素贝叶斯模型、隐马尔可夫模型的非监督学习也是极大似然估计或极大后验概率估计,但这时模型含有隐变量。
学习算法
统计学习的问题有了具体的形式以后,就变成了最优化问题。有时,最优化问题比较简单,解析解存在,最优解可以由公式简单计算。但在多数情况下,最优化问题没有解析解,需要用数值计算的方法或启发式的方法求解。
朴素贝叶斯法与隐马尔可夫模型的监督学习,最优解即极大似然估计值,可以由概率计算公式直接计算。
感知机、逻辑斯谛回归与最大熵模型、条件随机场的学习利用梯度下降法、拟牛顿法等。这些都是一般的无约束最优化问题的解法。
支持向量机学习,可以解凸二次规划的对偶问题。有序列最小最优化算法等方法。
决策树学习是基于启发式算法的典型例子。可以认为特征选择、生成、剪枝是启发式地进行正则化的极大似然估计。
提升方法利用学习的模型是加法模型、损失函数是指数损失函数的特点,启发式地从前向后逐步学习模型,以达到逼近优化目标函数的目的。
EM算法是一种迭代的求解含隐变量概率模型参数的方法,它的收敛性可以保证,但是不能保证收敛到全局最优。
支持向量机学习、逻辑斯谛回归与最大熵模型学习、条件随机场学习是凸优化问题,全局最优解保证存在。而其他学习问题则不是凸优化问题。
基本问题 :聚类 (clustering)是将样本集合中相似的样本归到相同的类,相似的定义一般用距离度量。∑ i = 1 N p ( z i ∣ x i ) = 1 \sum_{i=1}^N p(z_i|x_i) =1 ∑ i = 1 N p ( z i ∣ x i ) = 1
降维 (dimensionality reduction)是将样本集合中的样本(实例)从高维空间转换到低维空间。维度灾难 (前面章节有讲到)等
概率模型估计 (probability model estimation),简称概率估计,假设训练数据由一个概率模型生成,由训练数据学习概率模型的结构和参数。
无监督学习方法
同监督学习一样,无监督学习也有三要素 :模型、策略、算法模型 就是函数z = g θ ( x ) z=g_\theta(x) z = g θ ( x ) P θ ( z ∣ x ) P_\theta(z |x) P θ ( z ∣ x ) P θ ( x ∣ z ) P_\theta(x|z) P θ ( x ∣ z )
聚类 中模型的输出是 类别
降维 中模型的输出是 低维向量
概率模型估计 中的模型可以是混合概率模型,也可以是有向概率图模型和无向概率图模型
策略 在不同的问题中有不同的形式,但都可以表示为目标函数的优化
聚类 中样本与所属类别中心距离的最小化
降维 中样本从高维空间转换到低维空间过程中信息损失的最小化
概率模型估计 中模型生成数据概率的最大化
算法 通常是迭代算法,通过迭代达到目标函数的最优化,比如,梯度下降法。
层次聚类法、k均值聚类 是硬聚类方法
高斯混合模型 EM算法是软聚类方法
主成分分析、潜在语义分析 是降维方法
概率潜在语义分析、潜在狄利克雷分配 是概率模型估计方法
[13-1] Hastie T, Tibshirani R, Friedman J. The elements of statistical learning:data mining, inference, and prediction. Springer. 2001.
[13-2] Bishop M. Pattern Recognition and Machine Learning. Springer, 2006.
[13-3] Koller D, Friedman N. Probabilistic graphical models: principles and techniques. Cambridge, MA: MIT Press, 2009.
[13-4] Goodfellow I,Bengio Y,Courville A. Deep learning. Cambridge, MA: MIT Press, 2016.
[13-5] Michelle T M. Machine Learning. McGraw-Hill Companies, Inc. 1997.(中译本:机器学习。北京:机械工业出版社,2003.)
[13-6] Barber D. Bayesian reasoning and machine learning, Cambridge, UK:Cambridge University Press, 2012.
[13-7] 周志华. 机器学习. 北京:清华大学出版社,2017.
聚类分析(Cluster analysis or clustering )是针对给定的样本,根据它们特征点的相似度(距离),将其归并到若干个类(簇)中的分析问题。聚类分析本身不是一种特定的算法,而是要解决的一般任务。
Hard clusteringfuzzy clustering )
Connectivity models:如 hierarchical clustering 基于距离连通性(based on distance connectivity)
聚类分析算法(Cluster analysis algorithms ):sklearn中的聚类算法和介绍 基于连接的聚类(层次聚类) Connectivity-based clustering(Hierarchical clustering ):
距离度量或相似度
合并规则(cluster间的距离规则,cluster间的距离可以是最短、最长、中心距离、平均距离等)
停止条件(达到k值,也就是cluster的个数达到阈值;cluster的直径达到阈值;)
DIANA (DIvisive ANAlysis Clustering) algorithm
基于质心的聚类 Centroid-based clustering:
基于分布的聚类 Distribution-based clustering:
基于密度的聚类 Density-based clustering:
基于网格的聚类 Grid-based clustering:其它聚类 :
高效聚类 :
高维数据的聚类 (Clustering high-dimensional data ):
投影聚类Projected clustering
聚类结果的评估与聚类本身一样困难(并不像计算错误数量或监督分类算法的精度和召回率那么简单)。一般分为Internal evaluation和External evaluation,当两种评估效果都不好时就需要human evaluation。
先作一些定义:
数据集D = { x 1 , x 2 , . . . , x i , . . . , x j , . . . , x n } D=\{x_1,x_2,...,x_i,...,x_j,...,x_n\} D = { x 1 , x 2 , ... , x i , ... , x j , ... , x n }
设T T T C p C_p C p d i s t ( x i , x j ) ≤ T dist(x_i,x_j) \leq T d i s t ( x i , x j ) ≤ T C p C_p C p
C = { C 1 , C 2 , . . . , C k } C = \{C_1,C_2,...,C_k\} C = { C 1 , C 2 , ... , C k } C ∗ = { C 1 ∗ , C 2 ∗ , . . . , C s ∗ } C^* = \{C_1^*,C_2^*,...,C_s^*\} C ∗ = { C 1 ∗ , C 2 ∗ , ... , C s ∗ } λ \lambda λ C C C λ = [ 0 , 1 , . . . , k ] , λ ∗ = [ 0 , 1 , . . . , s ] \lambda = [0,1,...,k],\lambda^* = [0,1,...,s] λ = [ 0 , 1 , ... , k ] , λ ∗ = [ 0 , 1 , ... , s ] n n n λ i \lambda_i λ i x i x_i x i a = T P , T P = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } a = TP, TP=\{(x_i,x_j)\mid\lambda_i = \lambda_j, \lambda_i^* = \lambda_j^* ,i \lt j\} a = TP , TP = {( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } C C C C ∗ C^* C ∗ b = T N , T N = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ ≠ λ j ∗ , i < j } b = TN, TN=\{(x_i,x_j)\mid\lambda_i = \lambda_j, \lambda_i^* \neq \lambda_j^* ,i \lt j\} b = TN , TN = {( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } C C C C ∗ C^* C ∗ c = F P , F P = { ( x i , x j ) ∣ λ i ≠ λ j , λ i ∗ = λ j ∗ , i < j } c = FP, FP=\{(x_i,x_j)\mid\lambda_i \neq \lambda_j, \lambda_i^* = \lambda_j^* ,i\lt j\} c = FP , FP = {( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } C C C C ∗ C^* C ∗ d = F N , F N = { ( x i , x j ) ∣ λ i ≠ λ j , λ i ∗ ≠ λ j ∗ , i < j } d = FN, FN=\{(x_i,x_j) \mid \lambda_i \neq \lambda_j, \lambda_i^* \neq \lambda_j^* ,i\lt j\} d = FN , FN = {( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j } C C C C ∗ C^* C ∗
注意:labels_pred = [0, 0, 1, 1] 与 labels_true = [0, 0, 1, 1] 以及 labels_pred = [0, 0, 1, 1] 与 labels_true = [1, 1, 0, 0] 是没有区别的,他们都正确的聚类了。
样本对的数量为C n 2 = ( n 2 ) = n ( n − 1 ) / 2 = a + b + c + d C_n^2 = \binom{n}{2} =n(n-1)/2 = a+b+c+d C n 2 = ( 2 n ) = n ( n − 1 ) /2 = a + b + c + d C C C
d i j = d i s t ( x i , x j ) d_{ij} = dist(x_i,x_j) d ij = d i s t ( x i , x j ) x i , x j x_i,x_j x i , x j
n p = ∣ C p ∣ n_p = |C_p| n p = ∣ C p ∣ C p C_p C p x ˉ p = 1 n p ∑ x i ∈ C p x i \bar{x}_p = \frac{1}{n_p}\sum_{x_i \in C_p}x_i x ˉ p = n p 1 ∑ x i ∈ C p x i C p C_p C p d i a m ( C p ) = max { d i s t ( x i , x j ) ∣ x i , x j ∈ C p } diam(C_p) = \max \{dist(x_i,x_j) \mid x_i,x_j \in C_p\} d iam ( C p ) = max { d i s t ( x i , x j ) ∣ x i , x j ∈ C p } a v g ( C p ) = 2 n p ( n p − 1 ) ∑ 1 ≤ i < j ≤ n p d i s t ( x i , x j ) avg(C_p) = \frac{2}{n_p(n_p-1)} \sum_{1\leq i \lt j\leq n_p }dist(x_i,x_j) a vg ( C p ) = n p ( n p − 1 ) 2 ∑ 1 ≤ i < j ≤ n p d i s t ( x i , x j ) A C p = ∑ x i ∈ C p ( x i − x ˉ p ) ( x i − x ˉ p ) T A_{C_p} = \sum_{x_i \in C_p} (x_i-\bar{x}_p)(x_i-\bar{x}_p)^T A C p = ∑ x i ∈ C p ( x i − x ˉ p ) ( x i − x ˉ p ) T scatter matrix )S C p = 1 n p − 1 A C p S_{C_p} = \frac{1}{n_p-1}A_{C_p} S C p = n p − 1 1 A C p covariance matrix )
两个簇之间的距离主要有以下表示方法:d m i n ( C p , C q ) = min { d i s t ( x i , x j ) ∣ x i ∈ C p , x j ∈ C q } d_{min}(C_p,C_q) = \min\{dist(x_i,x_j) \mid x_i \in C_p,x_j \in C_q\} d min ( C p , C q ) = min { d i s t ( x i , x j ) ∣ x i ∈ C p , x j ∈ C q } d m a x ( C p , C q ) = max { d i s t ( x i , x j ) ∣ x i ∈ C p , x j ∈ C q } d_{max}(C_p,C_q) = \max\{dist(x_i,x_j) \mid x_i \in C_p,x_j \in C_q\} d ma x ( C p , C q ) = max { d i s t ( x i , x j ) ∣ x i ∈ C p , x j ∈ C q } d c e n ( C p , C q ) = d i s t ( x ˉ p , x ˉ q ) d_{cen}(C_p,C_q) = dist(\bar{x}_p,\bar{x}_q) d ce n ( C p , C q ) = d i s t ( x ˉ p , x ˉ q ) d m e a n ( C p , C q ) = 1 n p n q ∑ x i ∈ G p ∑ x j ∈ G q d i s t ( x i , x j ) d_{mean}(C_p,C_q) = \frac{1}{n_p n_q}\sum_{x_i \in G_p}\sum_{x_j \in G_q} dist(x_i,x_j) d m e an ( C p , C q ) = n p n q 1 ∑ x i ∈ G p ∑ x j ∈ G q d i s t ( x i , x j )
聚类标准(Clustering criteria ):簇内相似度(intra-cluster similarity)高,簇间相似度(inter-cluster similarity)低
确定数据集中的簇数 (Determining the number of clusters in a data set ),也就是K值的选取。k ≈ n / 2 k \thickapprox \sqrt{n/2} k ≈ n /2
肘方法(Elbow method )
X-means clustering
Information criterion approach
Information–theoretic approach
轮廓系数(Silhouette method )
Cross-validation
Finding number of clusters in text databases
Analyzing the kernel matrix
Internal evaluation :
DB指数 (Davies-Bouldin Index, DBI )D B I = 1 k ∑ i = 1 k max j ≠ i ( a v g ( C i ) + a v g ( C j ) d c e n ( C i , C j ) ) DBI={\frac {1}{k}}\sum _{i=1}^{k}\max _{j\neq i}\left({\frac {avg(C_i)+avg(C_j)}{d_{cen}(C_{i},C_{j})}}\right) D B I = k 1 i = 1 ∑ k j = i max ( d ce n ( C i , C j ) a vg ( C i ) + a vg ( C j ) ) a v g ( C i ) avg(C_i) a vg ( C i ) d c e n ( C i , C j ) d_{cen}(C_{i},C_{j}) d ce n ( C i , C j )
metrics.davies_bouldin_score
轮廓系数 (Silhouette coefficient )a ( x i ) = 1 ∣ C p ∣ − 1 ∑ x i , x j ∈ C p , i ≠ j d i s t ( x i , x j ) {\displaystyle a(x_i)={\frac {1}{|C_{p}|-1}}\sum _{x_i,x_j\in C_{p},i\neq j}dist(x_i,x_j)} a ( x i ) = ∣ C p ∣ − 1 1 x i , x j ∈ C p , i = j ∑ d i s t ( x i , x j ) a ( x i ) a(x_i) a ( x i ) C p C_{p} C p b ( x i ) = min q ≠ p 1 ∣ C q ∣ ∑ x i ∈ C p , x j ∈ C q d i s t ( x i , x j ) {\displaystyle b(x_i)=\min _{q\neq p}{\frac {1}{|C_{q}|}}\sum _{x_i\in C_{p},x_j\in C_{q}}dist(x_i,x_j) } b ( x i ) = q = p min ∣ C q ∣ 1 x i ∈ C p , x j ∈ C q ∑ d i s t ( x i , x j ) C p C_{p} C p x i x_i x i C q C_{q} C q b ( x i ) b(x_i) b ( x i ) x i x_i x i s ( x i ) = b ( x i ) − a ( x i ) max { a ( x i ) , b ( x i ) } , x i ∈ C p , if ∣ C p ∣ > 1 {\displaystyle s(x_i)={\frac {b(x_i)-a(x_i)}{\max\{a(x_i),b(x_i)\}}}} ,x_i \in C_p , \text{if } |C_p| > 1 s ( x i ) = max { a ( x i ) , b ( x i )} b ( x i ) − a ( x i ) , x i ∈ C p , if ∣ C p ∣ > 1 s ( i ) = { 1 − a ( i ) / b ( i ) , if a ( i ) < b ( i ) 0 , if a ( i ) = b ( i ) b ( i ) / a ( i ) − 1 , if a ( i ) > b ( i ) s(i) = \begin{cases}
1-a(i)/b(i), & \text{if } a(i) < b(i) \\
0, & \text{if } a(i) = b(i) \\
b(i)/a(i)-1, & \text{if } a(i) > b(i) \\
\end{cases} s ( i ) = ⎩ ⎨ ⎧ 1 − a ( i ) / b ( i ) , 0 , b ( i ) / a ( i ) − 1 , if a ( i ) < b ( i ) if a ( i ) = b ( i ) if a ( i ) > b ( i ) S C = max k s ~ ( k ) {\displaystyle SC=\max _{k}{\tilde {s}}\left(k\right)} SC = k max s ~ ( k ) s ~ ( k ) {\displaystyle {\tilde {s}}\left(k\right)} s ~ ( k )
metrics.silhouette_score
Dunn指数 (Dunn index, DI )D I = min 1 ≤ i ≤ k { min j ≠ i ( d m i n ( C i , C j ) max 1 ≤ l ≤ k d i a m ( C l ) ) } DI=\min_{1\leq i\leq k}\bigg\{ \min_{j\neq i}\bigg(\frac{d_{min}(C_i,C_j)}{\max_{1\leq l \leq k}diam(C_l)}\bigg) \bigg\} D I = 1 ≤ i ≤ k min { j = i min ( max 1 ≤ l ≤ k d iam ( C l ) d min ( C i , C j ) ) }
CH指数 (Calinski-Harabasz Index )s = t r ( B k ) / k − 1 t r ( W k ) / n E − k = t r ( B k ) t r ( W k ) × n E − k k − 1 s = \frac{\mathrm{tr}(B_k)/{k - 1}}{\mathrm{tr}(W_k) / {n_E - k}} = \frac{\mathrm{tr}(B_k)}{\mathrm{tr}(W_k)} \times \frac{n_E - k}{k - 1} s = tr ( W k ) / n E − k tr ( B k ) / k − 1 = tr ( W k ) tr ( B k ) × k − 1 n E − k B k B_k B k W k W_k W k W k = ∑ q = 1 k ∑ x ∈ C q ( x − c q ) ( x − c q ) T W_k = \sum_{q=1}^k \sum_{x \in C_q} (x - c_q) (x - c_q)^T W k = q = 1 ∑ k x ∈ C q ∑ ( x − c q ) ( x − c q ) T B k = ∑ q = 1 k n q ( c q − c E ) ( c q − c E ) T B_k = \sum_{q=1}^k n_q (c_q - c_E) (c_q - c_E)^T B k = q = 1 ∑ k n q ( c q − c E ) ( c q − c E ) T t r ( B k ) \mathrm{tr}(B_k) tr ( B k ) C q C_q C q q q q c q c_q c q q q q c E c_E c E E E E n q n_q n q q q q E E E n E n_E n E E E E k k k
metrics.calinski_harabasz_score
External evaluation (就是需要人为标记每个样本所属的类)
纯度(Purity)C = { c i ∣ i = 1 , … , n } C = \{c_i|i=1,…,n \} C = { c i ∣ i = 1 , … , n } K = { k i ∣ 1 , … , m } K= \{k_i|1,…,m\} K = { k i ∣1 , … , m } 1 N ∑ k i ∈ K max c j ∈ C ∣ k i ∩ c j ∣ {\displaystyle {\frac {1}{N}}\sum _{k_i\in K}\max _{c_j\in C}{|k_i\cap c_j|}} N 1 k i ∈ K ∑ c j ∈ C max ∣ k i ∩ c j ∣
F-score P ( precision rate ) = T P T P + F P , R ( recall rate ) = T P T P + F N P(\text{precision rate})={\frac {TP}{TP+FP}}, R(\text{recall rate})={\frac {TP}{TP+FN}} P ( precision rate ) = TP + FP TP , R ( recall rate ) = TP + FN TP F β = ( β 2 + 1 ) ⋅ P ⋅ R β 2 ⋅ P + R F_{\beta }={\frac {(\beta ^{2}+1)\cdot P\cdot R}{\beta ^{2}\cdot P+R}} F β = β 2 ⋅ P + R ( β 2 + 1 ) ⋅ P ⋅ R β = 1 \beta = 1 β = 1 β = 0 , F 0 = P \beta = 0, F_0=P β = 0 , F 0 = P
Precision and recall
Jaccard index Jaccard index = J ( A , B ) = ∣ A ∩ B ∣ ∣ A ∪ B ∣ = T P T P + F P + F N {\displaystyle {\text{Jaccard index}}=J(A,B)={\frac {|A\cap B|}{|A\cup B|}}={\frac {TP}{TP+FP+FN}}} Jaccard index = J ( A , B ) = ∣ A ∪ B ∣ ∣ A ∩ B ∣ = TP + FP + FN TP
metrics.jaccard_score
Dice index D S C = 2 T P 2 T P + F P + F N {\displaystyle DSC={\frac {2TP}{2TP+FP+FN}}} D SC = 2 TP + FP + FN 2 TP
Homogeneity, completeness and V-measure C = { c i ∣ i = 1 , … , n } C = \{c_i|i=1,…,n \} C = { c i ∣ i = 1 , … , n } K = { k i ∣ 1 , … , m } K= \{k_i|1,…,m\} K = { k i ∣1 , … , m } A = [ a i j ] n × m A = [a_{ij}]_{n \times m} A = [ a ij ] n × m a i j a_{ij} a ij c i c_i c i k j k_j k j h = 1 − H ( C ∣ K ) H ( C ) , c = 1 − H ( K ∣ C ) H ( K ) h = 1 - \frac{H(C|K)}{H(C)} , c = 1 - \frac{H(K|C)}{H(K)} h = 1 − H ( C ) H ( C ∣ K ) , c = 1 − H ( K ) H ( K ∣ C ) H ( C ∣ K ) = − ∑ k = 1 ∣ K ∣ ∑ c = 1 ∣ C ∣ a c k N ⋅ log ( a c k ∑ c = 1 ∣ C ∣ a c k ) , H ( C ) = − ∑ c = 1 ∣ C ∣ ∑ k = 1 ∣ K ∣ a c k N ⋅ log ( ∑ k = 1 ∣ K ∣ a c k N ) H(C|K) = - \sum_{k=1}^{|K|} \sum_{c=1}^{|C|} \frac{a_{ck}}{N}
\cdot \log\left(\frac{a_{ck}}{\sum_{c=1}^{|C|}a_{ck}}\right) \quad,\quad H(C) = - \sum_{c=1}^{|C|} \frac{\sum_{k=1}^{|K|}a_{ck}}{N} \cdot \log\left(\frac{\sum_{k=1}^{|K|}a_{ck}}{N}\right) H ( C ∣ K ) = − k = 1 ∑ ∣ K ∣ c = 1 ∑ ∣ C ∣ N a c k ⋅ log ( ∑ c = 1 ∣ C ∣ a c k a c k ) , H ( C ) = − c = 1 ∑ ∣ C ∣ N ∑ k = 1 ∣ K ∣ a c k ⋅ log ( N ∑ k = 1 ∣ K ∣ a c k ) H ( K ∣ C ) = − ∑ c = 1 ∣ C ∣ ∑ k = 1 ∣ K ∣ a c k N ⋅ log ( a c k ∑ k = 1 ∣ K ∣ a c k ) , H ( K ) = − ∑ k = 1 ∣ K ∣ ∑ c = 1 ∣ C ∣ a c k N ⋅ log ( ∑ c = 1 ∣ C ∣ a c k N ) H(K|C) = - \sum_{c=1}^{|C|} \sum_{k=1}^{|K|} \frac{a_{ck}}{N}
\cdot \log\left(\frac{a_{ck}}{\sum_{k=1}^{|K|}a_{ck}}\right) \quad,\quad H(K) = - \sum_{k=1}^{|K|} \frac{\sum_{c=1}^{|C|}a_{ck}}{N} \cdot \log\left(\frac{\sum_{c=1}^{|C|}a_{ck}}{N}\right) H ( K ∣ C ) = − c = 1 ∑ ∣ C ∣ k = 1 ∑ ∣ K ∣ N a c k ⋅ log ( ∑ k = 1 ∣ K ∣ a c k a c k ) , H ( K ) = − k = 1 ∑ ∣ K ∣ N ∑ c = 1 ∣ C ∣ a c k ⋅ log ( N ∑ c = 1 ∣ C ∣ a c k ) 当 H ( C ) = 0 时, h = 1 ;当 H ( K ) = 0 时, c = 1 ; 当H(C)=0时,h=1;当H(K)=0时,c=1; 当 H ( C ) = 0 时, h = 1 ;当 H ( K ) = 0 时, c = 1 ; v = ( 1 + β ) × homogeneity × completeness ( β × homogeneity + completeness ) v = \frac{(1 + \beta) \times \text{homogeneity} \times \text{completeness}}{(\beta \times \text{homogeneity} + \text{completeness})} v = ( β × homogeneity + completeness ) ( 1 + β ) × homogeneity × completeness β \beta β β > 1 \beta>1 β > 1 参考
metrics.homogeneity_score, metrics.completeness_score, metrics.v_measure_score
Rand指数 (Rand index )R I = T P + T N T P + F P + F N + T N = a + d n ( n − 1 ) / 2 RI={\frac {TP+TN}{TP+FP+FN+TN}}=\frac{a+d}{n(n-1)/2} R I = TP + FP + FN + TN TP + TN = n ( n − 1 ) /2 a + d
衡量两个数据聚类之间相似性的度量(也可以是标记数据和预测数据之间的相似性)
FM指数(Fowlkes–Mallows index )FMI = TP ( TP + FP ) ( TP + FN ) \text{FMI} = \frac{\text{TP}}{\sqrt{(\text{TP} + \text{FP}) (\text{TP} + \text{FN})}} FMI = ( TP + FP ) ( TP + FN ) TP
metrics.fowlkes_mallows_score
from sklearn.metrics.cluster import contingency_matrix
x = ["a", "a", "a", "b", "b", "b"]
y = [0, 0, 1, 1, 2, 2]
contingency_matrix(x, y)
array([[2, 1, 0],
[0, 1, 2]])
列数代表y中不重复的个数;行代表x中不重复的个数;
metrics.cluster.contingency_matrix
行Predicted (expectation)
Actual\Predicted
P
N
P(positive)
TP
FN
N(negative)
FP
TN
注意正常的confusion matrix中的四个元素相加为C n 2 = n ( n − 1 ) / 2 C_n^2=n(n-1)/2 C n 2 = n ( n − 1 ) /2 ( n − 1 ) (n-1) ( n − 1 ) C = [ C 00 ( F N ) C 01 ( F P ) C 10 ( T N ) C 11 ( T P ) ] \begin{split}C = \left[\begin{matrix}
C_{00}(FN) & C_{01}(FP) \\
C_{10}(TN) & C_{11}(TP)
\end{matrix}\right]\end{split} C = [ C 00 ( FN ) C 10 ( TN ) C 01 ( FP ) C 11 ( TP ) ]
互信息 (mutual information )S = { s 1 , s 2 , … s N } S=\{s_{1},s_{2},\ldots s_{N}\} S = { s 1 , s 2 , … s N } U = { U 1 , U 2 , … , U R } U=\{U_{1},U_{2},\ldots ,U_{R}\} U = { U 1 , U 2 , … , U R } V = { V 1 , V 2 , … , V C } V=\{V_{1},V_{2},\ldots ,V_{C}\} V = { V 1 , V 2 , … , V C } U i ∩ U j = ∅ = V i ∩ V j {\displaystyle U_{i}\cap U_{j}=\varnothing =V_{i}\cap V_{j}} U i ∩ U j = ∅ = V i ∩ V j ∪ i = 1 R U i = ∪ j = 1 C V j = S \cup _{{i=1}}^{R}U_{i}=\cup _{{j=1}}^{C}V_{j}=S ∪ i = 1 R U i = ∪ j = 1 C V j = S M = [ n i j ] j = 1 … C i = 1 … R M=[n_{{ij}}]_{{j=1\ldots C}}^{{i=1\ldots R}} M = [ n ij ] j = 1 … C i = 1 … R contingency table ,其中n i j = ∣ U i ∩ V j ∣ n_{{ij}}=\left|U_{i}\cap V_{j}\right| n ij = ∣ U i ∩ V j ∣ P U ( i ) = ∣ U i ∣ N {\displaystyle P_{U}(i)={\frac {|U_{i}|}{N}}} P U ( i ) = N ∣ U i ∣ U i U_i U i P U V ( i , j ) = ∣ U i ∩ V j ∣ N {\displaystyle P_{UV}(i,j)={\frac {|U_{i}\cap V_{j}|}{N}}} P U V ( i , j ) = N ∣ U i ∩ V j ∣ U i , V j U_i, V_j U i , V j H ( U ) = − ∑ i = 1 R P U ( i ) log P U ( i ) {\displaystyle H(U)=-\sum _{i=1}^{R}P_{U}(i)\log P_{U}(i)} H ( U ) = − i = 1 ∑ R P U ( i ) log P U ( i ) U U U M I ( U , V ) = ∑ i = 1 R ∑ j = 1 C P U V ( i , j ) log P U V ( i , j ) P U ( i ) P V ( j ) {\displaystyle MI(U,V)=\sum _{i=1}^{R}\sum _{j=1}^{C}P_{UV}(i,j)\log {\frac {P_{UV}(i,j)}{P_{U}(i)P_{V}(j)}}} M I ( U , V ) = i = 1 ∑ R j = 1 ∑ C P U V ( i , j ) log P U ( i ) P V ( j ) P U V ( i , j ) NMI ( U , V ) = MI ( U , V ) mean ( H ( U ) , H ( V ) ) \text{NMI}(U, V) = \frac{\text{MI}(U, V)}{\text{mean}(H(U), H(V))} NMI ( U , V ) = mean ( H ( U ) , H ( V )) MI ( U , V ) A M I ( U , V ) = M I ( U , V ) − E { M I ( U , V ) } max { H ( U ) , H ( V ) } − E { M I ( U , V ) } AMI(U,V)={\frac {MI(U,V)-E\{MI(U,V)\}}{\max {\{H(U),H(V)\}}-E \{MI(U,V)\}}} A M I ( U , V ) = max { H ( U ) , H ( V )} − E { M I ( U , V )} M I ( U , V ) − E { M I ( U , V )} E { M I ( U , V ) } = ∑ i = 1 R ∑ j = 1 C ∑ n i j = ( a i + b j − N ) + min ( a i , b j ) n i j N log ( N ⋅ n i j a i b j ) × a i ! b j ! ( N − a i ) ! ( N − b j ) ! N ! n i j ! ( a i − n i j ) ! ( b j − n i j ) ! ( N − a i − b j + n i j ) ! {\begin{aligned}E\{MI(U,V)\}=&\sum _{{i=1}}^{R}\sum _{{j=1}}^{C}\sum _{{n_{{ij}}=(a_{i}+b_{j}-N)^{+}}}^{{\min(a_{i},b_{j})}}{\frac {n_{{ij}}}{N}}\log \left({\frac {N\cdot n_{{ij}}}{a_{i}b_{j}}}\right)\times \\&{\frac {a_{i}!b_{j}!(N-a_{i})!(N-b_{j})!}{N!n_{{ij}}!(a_{i}-n_{{ij}})!(b_{j}-n_{{ij}})!(N-a_{i}-b_{j}+n_{{ij}})!}}\\\end{aligned}} E { M I ( U , V )} = i = 1 ∑ R j = 1 ∑ C n ij = ( a i + b j − N ) + ∑ m i n ( a i , b j ) N n ij log ( a i b j N ⋅ n ij ) × N ! n ij ! ( a i − n ij )! ( b j − n ij )! ( N − a i − b j + n ij )! a i ! b j ! ( N − a i )! ( N − b j )! E { M I ( U , V ) } 为 M I ( U , V ) E\{MI(U,V)\} 为MI(U,V) E { M I ( U , V )} 为 M I ( U , V ) ( a i + b j − N ) + = max ( 1 , a i + b j − N ) (a_{i}+b_{j}-N)^{+} = \max(1,a_{i}+b_{j}-N) ( a i + b j − N ) + = max ( 1 , a i + b j − N ) a i = ∑ j = 1 C n i j a_{i}=\sum _{{j=1}}^{C}n_{{ij}} a i = ∑ j = 1 C n ij b j = ∑ i = 1 R n i j b_{j}=\sum _{{i=1}}^{R}n_{{ij}} b j = ∑ i = 1 R n ij
参考Adjusted mutual information
Cluster tendency (聚类趋势)
霍普金斯统计量 (Hopkins statistic )X = { x 1 , x 2 , . . . , x n } , x i ∈ R d X=\{x_1,x_2,...,x_n\},x_i \in \mathbb{R}^d X = { x 1 , x 2 , ... , x n } , x i ∈ R d Y = { y 1 , y 2 , . . . , y m } , m ≪ n Y=\{y_1,y_2,...,y_m\}, m \ll n Y = { y 1 , y 2 , ... , y m } , m ≪ n u i = min d i s t ( y i , x j ∈ X ) u_{i} = \min dist(y_i,x_j\in X) u i = min d i s t ( y i , x j ∈ X ) w i = min d i s t ( x i , x j ∈ X i ≠ j ) w_{i} = \min dist(x_i,x_j\in X_{i\neq j}) w i = min d i s t ( x i , x j ∈ X i = j ) H = ∑ i = 1 m u i d ∑ i = 1 m u i d + ∑ i = 1 m w i d , {\displaystyle H={\frac {\sum _{i=1}^{m}{u_{i}^{d}}}{\sum _{i=1}^{m}{u_{i}^{d}}+\sum _{i=1}^{m}{w_{i}^{d}}}}\,,} H = ∑ i = 1 m u i d + ∑ i = 1 m w i d ∑ i = 1 m u i d , ∑ u ≫ ∑ w \sum u \gg \sum w ∑ u ≫ ∑ w
参考Clustering performance evaluation 以及Evaluation and assessment
k-means: 样本集合X = { x 1 , x 2 , . . . , x n } , x i ∈ R m X=\{x_1,x_2,...,x_n\},x_i \in \mathbb{R}^m X = { x 1 , x 2 , ... , x n } , x i ∈ R m C = { C 1 , . . . , C k } , k < n , C i ∩ C j = ∅ , ∪ i = 1 k C i = X C = \{ C_1,...,C_k\},k \lt n,C_i \cap C_j =\empty , \cup_{i=1}^kC_i =X C = { C 1 , ... , C k } , k < n , C i ∩ C j = ∅ , ∪ i = 1 k C i = X F : x i → l , l ∈ { 1 , . . . , k } F: x_i \to l,l\in \{1,...,k\} F : x i → l , l ∈ { 1 , ... , k }
模型 :l = F ( x i ) = F ( i ) , i ∈ { 1 , . . . , n } l = F(x_i) = F(i) ,i \in \{1,...,n\} l = F ( x i ) = F ( i ) , i ∈ { 1 , ... , n }
策略 :F ∗ = arg min F W ( F ) = arg min F ∑ l = 1 k ∑ F ( i ) = l n l ∥ x i − x ˉ l ∥ 2 F^* = \argmin_{F} W(F) = \argmin_{F} \sum_{l=1}^k \sum_{F(i)=l}^{n_l} \|x_i - \bar{x}_l\|^2 F ∗ = F arg min W ( F ) = F arg min l = 1 ∑ k F ( i ) = l ∑ n l ∥ x i − x ˉ l ∥ 2 W ( F ) W(F) W ( F ) n l = ∑ i = 1 n I ( F ( i ) = l ) n_l = \sum_{i=1}^n I(F(i)=l) n l = ∑ i = 1 n I ( F ( i ) = l )
n个样本分到k个cluster的所有分法的种类有S ( n , k ) S(n,k) S ( n , k ) S ( n , k ) = 1 k ! ∑ l = 1 k ( − 1 ) k − l ( k l ) k n S(n,k) = \frac{1}{k!}\sum_{l=1}^k(-1)^{k-l}\dbinom{k}{l}k^n S ( n , k ) = k ! 1 l = 1 ∑ k ( − 1 ) k − l ( l k ) k n
随机选择k个中心( m 1 , m 2 , . . . , m k ) (m_1,m_2,...,m_k) ( m 1 , m 2 , ... , m k )
将样本分别划分到与其最近的中心的cluster中
更新每个cluster的均值( m 1 , m 2 , . . . , m k ) (m_1,m_2,...,m_k) ( m 1 , m 2 , ... , m k )
重复2,3直到收敛(中心变化很小)
K-means算法有以下不足:
算法对初始值的选取依赖性极大。初始值不同,往往得到不同的局部极小值。
由于将均值点作为聚类中心进行新一轮计算,远离数据密集区的孤立点和噪声点会导致聚类中心偏离真正的数据密集区,所以K-均值算法对噪声点和孤立点很敏感。
K-mediods算法优缺点
解决了K-均值算法对初始值选择依赖度大的问题。K-均值算法对于不同的初始值,结果往往得到不同的局部极小值。而K-中心点轮换算法采用轮换替换的方法替换中心点,从而与初始值的选择没有关系。
解决了K-均值算法对噪声和离群点的敏感性问题。由于该算法不使用平均值来更改中心点而是选用位置最靠近中心的对象作为中心代表点,因此并不容易受极端数据的影响,具有很好的鲁棒性。
K-中心点轮换算法也存有以下缺点:
由于K-中心点轮换算法是基于划分的一种聚类算法,仍然要求输入要得到的簇的数目k,所以当k的取值不正确时,对聚类的结果影响甚大。
从以上的时间复杂度也可以看出,当n和k较大时,计算代价很高,所以将该算法应用于大数据集时不是很理想。
[14-1] Jain A, Dubes R. Algorithms for clustering data. Prentice-Hall, 1988.
[14-2] Aggarwal C C, Reddy C K. Data clustering: algorithms and applications. CRC Press, 2013.
[14-3] MacQueen J B. Some methods for classification and analysis of multivariate observations. Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Volume 1,pp.396-410. 1967.
[14-4] Hastie T,Tibshirani R,Friedman J. The Elements of Statistical Learning: DataMining,Inference,and Prediction . Springer. 2001(中译本:统计学习基础——数据挖掘、推理与预测。范明,柴玉梅,昝红英等译。北京:电子工业出版社,2004)
[14-5] Pelleg D, Moore A W. X-means: Extending K-means with Efficient Estimation of the Number of Clusters. Proceedings of ICML, pp. 727-734, 2000.
[14-6] Ester M, Kriegel H, Sander J, et al. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise . Proceedings of ACM SIGKDD, pp. 226-231, 1996.
[14-7] Shi J, Malik J. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000,22(8):888-905.
[14-8] Dhillon I S. Co-clustering documents and words using bipartite spectral graph partitioning. Proceedings of ACM SIGKDD, pp. 269-274. 2001.
奇异值分解(Singular Value Decomposition, SVD )是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算法的基石。也是矩阵分解(Matrix decomposition )的一种。
先了解下特征值分解(Eigenvalues and eigenvectors 以及Eigendecomposition of a matrix )以及对角化(Diagonalizable matrix )A u = λ u ⟹ ( A − I λ ) u = 0 {\displaystyle A\mathbf {u} =\lambda \mathbf {u} \implies (A-I\lambda)\mathbf {u} = 0} A u = λ u ⟹ ( A − I λ ) u = 0 A n × n A_{n\times n} A n × n q i q_i q i A = Q Λ Q − 1 {\displaystyle A=Q\Lambda Q^{-1}} A = Q Λ Q − 1 Λ \Lambda Λ diagonal matrix );q i q_i q i invertible )A − 1 = Q Λ − 1 Q − 1 {\displaystyle \mathbf {A} ^{-1}=\mathbf {Q} \mathbf {\Lambda } ^{-1}\mathbf {Q} ^{-1}} A − 1 = Q Λ − 1 Q − 1
注意只有可对角化 的矩阵分解才能用这种方式:如以下矩阵不可被对角化A = [ 1 1 0 1 ] {\displaystyle A = \left[{\begin{matrix}1&1\\0&1\end{matrix}}\right]} A = [ 1 0 1 1 ] [ 1 , 1 ] [1,1] [ 1 , 1 ] [ 1 , 0 ] T , [ − 1 , 0 ] T [1,0]^T , [-1,0]^T [ 1 , 0 ] T , [ − 1 , 0 ] T
如果 A \mathbf {A} A symmetric matrix ),因为Q \mathbf {Q} Q A \mathbf {A} A orthogonal matrix ),有Q − 1 = Q T {\displaystyle \mathbf {Q} ^{-1}=\mathbf {Q} ^{\mathrm {T} }} Q − 1 = Q T
Q其实也是酉矩阵(Unitary Matrix ),它是 正交矩阵 在复数上的推广。
不可对角化的矩阵称为有缺陷的(defective )。对于有缺陷的矩阵,特征向量的概念推广到广义特征向量(generalized eigenvectors ),特征值的对角矩阵推广到Jordan 范式(Jordan normal form )。在代数闭域上,任何矩阵A都具有Jordan 范式,因此允许广义特征向量的基和分解为广义特征空间(generalized eigenspaces )。
模型 :M m × n = U Σ V H M_{m \times n} = {\displaystyle \mathbf {U\Sigma V^{H}} } M m × n = UΣ V H M m × n = U Σ V T M_{m \times n} = {\displaystyle \mathbf {U\Sigma V^{T}} } M m × n = UΣ V T U U U m × m {\displaystyle m\times m} m × m Σ = d i a g ( σ 1 , σ 2 , . . . , σ p ) \Sigma = diag(\sigma_1,\sigma_2,...,\sigma_p) Σ = d ia g ( σ 1 , σ 2 , ... , σ p ) p = min ( m , n ) , σ 1 ≥ σ 2 ≥ . . . ≥ σ p ≥ 0 p=\min(m,n), \sigma_1 \ge \sigma_2 \ge ... \ge \sigma_p \ge 0 p = min ( m , n ) , σ 1 ≥ σ 2 ≥ ... ≥ σ p ≥ 0 V V V n × n {\displaystyle n\times n} n × n σ i \sigma_i σ i 奇异值 U U U V V V M M M r = r a n k ( M ) , r ≤ min ( m , n ) r = rank(M),r \le \min(m,n) r = r ank ( M ) , r ≤ min ( m , n ) M M M M m × n = U m × r Σ r × r V n × r T M_{m \times n} = U_{m \times r} \Sigma_{r \times r} V_{n \times r}^T M m × n = U m × r Σ r × r V n × r T r a n k ( Σ r × r ) = r a n k ( M ) = r rank(\Sigma_{r \times r}) = rank(M) = r r ank ( Σ r × r ) = r ank ( M ) = r M M M M m × n ≈ U m × k Σ k × k V n × k T , 0 < k < r M_{m \times n} \approx U_{m \times k} \Sigma_{k \times k} V_{n \times k}^T , 0 \lt k \lt r M m × n ≈ U m × k Σ k × k V n × k T , 0 < k < r M M M pseudoinverse )M + = V Σ + U H M^{+} = V\Sigma^{+}U^{H} M + = V Σ + U H M M M σ i \sigma_i σ i M T M M^TM M T M λ i \sqrt{\lambda_i} λ i V V V M T M M^TM M T M U U U M M T MM^T M M T M T M M^TM M T M λ \lambda λ M T M M^TM M T M ∥ M x ∥ 2 = x T A T A x = x T λ x = λ x T x = λ ∥ x ∥ 2 ⇒ λ = ∥ M x ∥ 2 ∥ x ∥ 2 ≥ 0 \|Mx\|^2 = x^TA^TAx = x^T \lambda x= \lambda x^Tx = \lambda\|x\|^2 \Rightarrow \lambda = \frac{\|Mx\|^2}{\|x\|^2} \ge 0 ∥ M x ∥ 2 = x T A T A x = x T λ x = λ x T x = λ ∥ x ∥ 2 ⇒ λ = ∥ x ∥ 2 ∥ M x ∥ 2 ≥ 0 M T M = V Σ T U T U Σ V T = V ( Σ T Σ ) V T M M T = U Σ V T V Σ T U T = U ( Σ Σ T ) U T {\begin{aligned}\mathbf {M} ^{T}\mathbf {M} &=\mathbf {V} {\boldsymbol {\Sigma }}^{T}\mathbf {U} ^{T}\,\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{T}=\mathbf {V} ({\boldsymbol {\Sigma }}^{T}{\boldsymbol {\Sigma }})\mathbf {V} ^{T}\\\mathbf {M} \mathbf {M} ^{T}&=\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{T}\,\mathbf {V} {\boldsymbol {\Sigma }}^{T}\mathbf {U} ^{T}=\mathbf {U} ({\boldsymbol {\Sigma }}{\boldsymbol {\Sigma }}^{T})\mathbf {U} ^{T}\end{aligned}} M T M M M T = V Σ T U T U Σ V T = V ( Σ T Σ ) V T = U Σ V T V Σ T U T = U ( Σ Σ T ) U T
策略 :
算法 :
这里介绍一些参见的矩阵 ,以及其性质。
共轭(Complex conjugate )是复数上的概念z = a + b i z =a + bi z = a + bi z ˉ = a − b i \bar{z} = a-bi z ˉ = a − bi z z ˉ = a 2 + b 2 z\bar{z} = a^2 + b^2 z z ˉ = a 2 + b 2 Adjugate matrix ,虽然有时候他们都用A ∗ A^* A ∗ A H A^H A H 共轭转置矩阵与伴随矩阵都用A*表示合理吗?
有个神奇的公式:欧拉公式 e π i + 1 = 0 e^{\pi i}+1=0 e πi + 1 = 0
( A H ) i j = A j i ‾ {\displaystyle \left({\boldsymbol {A}}^{\mathrm {H} }\right)_{ij}={\overline {{\boldsymbol {A}}_{ji}}}} ( A H ) ij = A ji
A H = ( A ‾ ) T = A T ‾ {\displaystyle {\boldsymbol {A}}^{\mathrm {H} }=\left({\overline {\boldsymbol {A}}}\right)^{\mathsf {T}}={\overline {{\boldsymbol {A}}^{\mathsf {T}}}}} A H = ( A ) T = A T
例如:A = [ 1 − 2 − i 5 1 + i i 4 − 2 i ] , A T = [ 1 1 + i − 2 − i i 5 4 − 2 i ] , A H = [ 1 1 − i − 2 + i − i 5 4 + 2 i ] {\displaystyle {\boldsymbol {A}}={\begin{bmatrix}1&-2-i&5\\1+i&i&4-2i\end{bmatrix}}} , {\displaystyle {\boldsymbol {A}}^{\mathsf {T}}={\begin{bmatrix}1&1+i\\-2-i&i\\5&4-2i\end{bmatrix}}} , {\displaystyle {\boldsymbol {A}}^{\mathrm {H} }={\begin{bmatrix}1&1-i\\-2+i&-i\\5&4+2i\end{bmatrix}}} A = [ 1 1 + i − 2 − i i 5 4 − 2 i ] , A T = ⎣ ⎡ 1 − 2 − i 5 1 + i i 4 − 2 i ⎦ ⎤ , A H = ⎣ ⎡ 1 − 2 + i 5 1 − i − i 4 + 2 i ⎦ ⎤
性质:
( A + B ) H = A H + B H {\displaystyle ({\boldsymbol {A}}+{\boldsymbol {B}})^{\mathrm {H} }={\boldsymbol {A}}^{\mathrm {H} }+{\boldsymbol {B }}^{\mathrm {H} }} ( A + B ) H = A H + B H ( z A ) H = z ‾ A H {\displaystyle (z{\boldsymbol {A}})^{\mathrm {H} }={\overline {z}}{\boldsymbol {A}}^{\mathrm {H} }} ( z A ) H = z A H ( A B ) H = B H A H {\displaystyle ({\boldsymbol {A}}{\boldsymbol {B}})^{\mathrm {H} }={\boldsymbol {B}}^{\mathrm {H} }{\boldsymbol {A}} ^{\mathrm {H} }} ( A B ) H = B H A H ( A H ) H = A {\displaystyle \left({\boldsymbol {A}}^{\mathrm {H} }\right)^{\mathrm {H} }={\boldsymbol {A}}} ( A H ) H = A 如果A A A A H A^H A H ( A H ) − 1 = ( A − 1 ) H {\displaystyle \left({\boldsymbol {A}}^{\mathrm {H} }\right)^{-1}=\left({\boldsymbol {A}}^{-1}\right)^{ \mathrm {H} }} ( A H ) − 1 = ( A − 1 ) H
A H A^H A H A A A 内积性质⟨ A x , y ⟩ m = ⟨ x , A H y ⟩ n {\displaystyle \left\langle {\boldsymbol {A}}x,y\right\rangle _{m}=\left\langle x,{\boldsymbol {A}}^{\mathrm {H} }y\right\rangle _{n}} ⟨ A x , y ⟩ m = ⟨ x , A H y ⟩ n A是m*n,x是n*1,y是m*1,下标m表示是m维向量作内积。
(A是方阵)行列式性质det ( A H ) = det ( A ) ‾ {\displaystyle \det \left({\boldsymbol {A}}^{\mathrm {H} }\right)={\overline {\det \left({\boldsymbol {A}}\right)}}} det ( A H ) = det ( A )
(A是方阵)迹的性质tr ( A H ) = tr ( A ) ‾ {\displaystyle \operatorname {tr} \left({\boldsymbol {A}}^{\mathrm {H} }\right)={\overline {\operatorname {tr} ({\boldsymbol {A}})}}} tr ( A H ) = tr ( A )
Hermitian matrix (or self-adjoint matrix)方阵 A Hermitian ⟺ A = A H {\displaystyle A{\text{ Hermitian}}\quad \iff \quad A=A^{\mathsf {H}}} A Hermitian ⟺ A = A H A = [ 0 a − i b c − i d a + i b 1 m − i n c + i d m + i n 2 ] A = {\displaystyle {\begin{bmatrix}0&a-ib&c-id\\a+ib&1&m-in\\c+id&m+in&2\end{bmatrix}}} A = ⎣ ⎡ 0 a + ib c + i d a − ib 1 m + in c − i d m − in 2 ⎦ ⎤ 埃尔米特矩阵是对称矩阵在复数上的推广 。
其矩阵有很多性质,具体见维基百科。
Skew-Hermitian matrix:A skew-Hermitian ⟺ A H = − A {\displaystyle A{\text{ skew-Hermitian}}\quad \iff \quad A^{\mathsf {H}}=-A} A skew-Hermitian ⟺ A H = − A
A是复方阵 A normal ⟺ A H A = A A H {\displaystyle A{\text{ normal}}\quad \iff \quad A^{H}A=AA^{H}} A normal ⟺ A H A = A A H
例子:A = [ 1 1 0 0 1 1 1 0 1 ] , A A H = [ 2 1 1 1 2 1 1 1 2 ] = A H A . {\displaystyle A={\begin{bmatrix}1&1&0\\0&1&1\\1&0&1\end{bmatrix}}} , {\displaystyle AA^{H}={\begin{bmatrix}2&1&1\\1&2&1\\1&1&2\end{bmatrix}}=A^{H}A.} A = ⎣ ⎡ 1 0 1 1 1 0 0 1 1 ⎦ ⎤ , A A H = ⎣ ⎡ 2 1 1 1 2 1 1 1 2 ⎦ ⎤ = A H A .
Normal matrix一定是可对角化的A = U Λ U H A = U\Lambda U^H A = U Λ U H U U U Λ = d i a g ( λ 1 , . . . ) \Lambda = diag(\lambda_1,...) Λ = d ia g ( λ 1 , ... ) A A A
对于复矩阵,所有的unitary, Hermitian, and skew-Hermitian 矩阵都是normal矩阵
U是复方阵 U H = U − 1 U^{H} = U^{-1} U H = U − 1
U H U = U U H = I , {\displaystyle U^{H}U=UU^{H}=I,} U H U = U U H = I , ⟨ U x , U y ⟩ = ⟨ x , y ⟩ \left\langle Ux,Uy\right\rangle = \left\langle x,y\right\rangle ⟨ Ux , U y ⟩ = ⟨ x , y ⟩ U是可对角化的U = V D V H , {\displaystyle U=VDV^{H},} U = V D V H ,
∣ det ( U ) ∣ = 1 {\displaystyle \left|\det(U)\right|=1} ∣ det ( U ) ∣ = 1 其特征向量是相互正交的(废话,正交矩阵的推广)
酉矩阵它是正交矩阵在复数上的推广 。
sympy.Matrix除了分解还有diagonalize对角化(也是一种矩阵分解),eig特征值(其实也可以特征值分解),rref行简化阶梯型,det行列式,inv逆矩阵,广义逆矩阵pinv;更多参考 参考 参考
除了SVD和PCA,还有很多矩阵分解(Matrix decomposition )的方法。不过有很多分解是有要求的,比如必须是方阵(特征值分解就要求必须是方阵)等。
类似的可以定义QL、RQ 和 LQ,L是下三角矩阵(left(lower) triangular matrix )
[15-1] Leon S J. Linear algebra with applications. Pearson, 2009(中译本:线性代数。张文博,张丽静 译. 北京:机械工业出版社)
[15-2] Strang G. Introduction to linear algebra. Fourth Edition. Wellesley-Cambridge Press, 2009.
[15-3] Cline A K. Dhillon I S. Computation of the singular value decomposition, Handbook of linear algebra. CRC Press, 2006.
[15-4] 徐树方. 矩阵计算的理论与方法。北京:北京大学出版社, 1995.
[15-5] Kolda T G,Bader B W. Tensor decompositions and applications . SIAM Review, 2009, 51(3):455-500.
主成分分析(Principal component analysis, PCA )是一种常用的无监督学习方法,PCA利用正交变换把由线性相关变量表示的观测数据转换为少数几个由线性无关变量表示的数据,线性无关的变量称为主成分。
主成分分析步骤如下:
对给定数据进行规范化,使得数据每一变量的平均值为0,方差为1(StandardScaler)。
对数据进行正交变换,原来由线性相关变量表示的数据,通过正交变换变成由若干个线性无关的新变量表示的数据。
新变量是可能的正交变换中变量的方差的和(信息保存)最大的,方差表示在新变量上信息的大小。将新变量依次称为第一主成分、第二主成分等。
我们通常表示一个样本是在实数空间中用正交坐标系表示,规范化的数据分布在原点附近
主成分分析就是对数据进行正交变换,对原坐标系进行旋转变换,并将数据在新坐标系中表示;我们将选择方差最大的方向作为新坐标系的第一坐标轴。方差最大代表着在该方向上的投影(不就是在这个坐标系的坐标轴上的表示么)分散的最开。
根据方差的定义,每个方向上方差就是在该坐标系(变换后的新坐标系)上表示所对应的维度的方差v a r ( a ) = 1 N − 1 ∑ i = 1 N ( a i − μ ) 2 var(a) = \frac{1}{N-1}\sum_{i=1}^N (a_i - \mu)^2 v a r ( a ) = N − 1 1 ∑ i = 1 N ( a i − μ ) 2 a a a v a r ( a ) = 1 N − 1 ∑ i = 1 N ( a i ) 2 var(a) = \frac{1}{N-1}\sum_{i=1}^N (a_i)^2 v a r ( a ) = N − 1 1 ∑ i = 1 N ( a i ) 2 a i a_i a i i i i x ( i ) x^{(i)} x ( i )
我们的目的就是为了v a r ( a ) var(a) v a r ( a ) v 1 v_1 v 1 T = { x ( 1 ) , x ( 2 ) , . . . , x ( N ) } , x = { x 1 , . . . , x m } T T = \{x^{(1)},x^{(2)},...,x^{(N)}\} , x=\{x_1,...,x_m\}^T T = { x ( 1 ) , x ( 2 ) , ... , x ( N ) } , x = { x 1 , ... , x m } T
max 1 N − 1 ∑ i = 1 N ⟨ x ( i ) , v 1 ⟩ 2 = 1 N − 1 ∑ i = 1 N ∥ x ( i ) T . v 1 ∥ 2 = 1 N − 1 ∑ i = 1 N ( x ( i ) T . v 1 ) T ( x ( i ) T . v 1 ) = 1 N − 1 ∑ i = 1 N v 1 T x ( i ) x ( i ) T v 1 = 1 N − 1 v 1 T ∑ i = 1 N [ x ( i ) x ( i ) T ] v 1 \max \frac{1}{N-1}\sum_{i=1}^N \braket{x^{(i)},v_1}^2 = \frac{1}{N-1}\sum_{i=1}^N \|{x^{(i)}}^{T}.v_1\|^2 \\= \frac{1}{N-1}\sum_{i=1}^N ({x^{(i)}}^{T}.v_1)^T({x^{(i)}}^{T}.v_1) \\= \frac{1}{N-1}\sum_{i=1}^N v_1^T{x^{(i)}}{x^{(i)}}^{T}v_1 \\= \frac{1}{N-1} v_1^T \sum_{i=1}^N[{x^{(i)}}{x^{(i)}}^{T}]v_1 max N − 1 1 i = 1 ∑ N ⟨ x ( i ) , v 1 ⟩ 2 = N − 1 1 i = 1 ∑ N ∥ x ( i ) T . v 1 ∥ 2 = N − 1 1 i = 1 ∑ N ( x ( i ) T . v 1 ) T ( x ( i ) T . v 1 ) = N − 1 1 i = 1 ∑ N v 1 T x ( i ) x ( i ) T v 1 = N − 1 1 v 1 T i = 1 ∑ N [ x ( i ) x ( i ) T ] v 1 X = [ x ( 1 ) , x ( 2 ) , . . . , x ( N ) ] X = [x^{(1)},x^{(2)},...,x^{(N)}] X = [ x ( 1 ) , x ( 2 ) , ... , x ( N ) ] X X T = ∑ i = 1 N [ x ( i ) x ( i ) T ] XX^T =\sum_{i=1}^N[{x^{(i)}}{x^{(i)}}^{T}] X X T = ∑ i = 1 N [ x ( i ) x ( i ) T ] max 1 N − 1 v 1 T X X T v 1 s . t . v 1 T v 1 = 1 \max \frac{1}{N-1} v_1^T XX^T v_1 \\ s.t. \quad v_1^Tv_1 =1 max N − 1 1 v 1 T X X T v 1 s . t . v 1 T v 1 = 1 矩阵求导 )L = − 1 N − 1 v 1 T X X T v 1 + λ 1 ( v 1 T v 1 − 1 ) L = - \frac{1}{N-1} v_1^T XX^T v_1 + \lambda_1(v_1^Tv_1 - 1) L = − N − 1 1 v 1 T X X T v 1 + λ 1 ( v 1 T v 1 − 1 ) ∂ L ∂ v 1 = − 2 1 N − 1 v 1 T X X T + 2 λ 1 v 1 T = 0 \frac{\partial L}{\partial v_1} = -2\frac{1}{N-1}v_1^T XX^T + 2\lambda_1 v_1^T =0 ∂ v 1 ∂ L = − 2 N − 1 1 v 1 T X X T + 2 λ 1 v 1 T = 0 1 N − 1 v 1 T X X T = λ 1 v 1 T ⟹ 1 N − 1 X X T v 1 = λ 1 v 1 \frac{1}{N-1}v_1^T XX^T = \lambda_1 v_1^T \implies \frac{1}{N-1}XX^Tv_1 = \lambda_1 v_1 N − 1 1 v 1 T X X T = λ 1 v 1 T ⟹ N − 1 1 X X T v 1 = λ 1 v 1 1 N − 1 X X T \frac{1}{N-1}XX^T N − 1 1 X X T X m × N X_{m \times N} X m × N Σ m × m \Sigma_{m \times m} Σ m × m
λ 1 \lambda_1 λ 1 Σ m × m \Sigma_{m \times m} Σ m × m v 1 v_1 v 1
接着求第二个主成分v 2 v_2 v 2 max 1 N − 1 v 2 T X X T v 2 s . t . v 2 T v 2 = 1 , v 2 T v 1 = 0 \max \frac{1}{N-1} v_2^T XX^T v_2 \\ s.t. \quad v_2^Tv_2 =1 ,v_2^Tv_1 =0 max N − 1 1 v 2 T X X T v 2 s . t . v 2 T v 2 = 1 , v 2 T v 1 = 0 v 1 T X X T v 2 = λ 1 v 1 T v 2 = 0 = v 2 T X X T v 1 = λ 1 v 2 T v 1 v_1^T XX^T v_2 = \lambda_1 v_1^T v_2 = 0 = v_2^T XX^T v_1 = \lambda_1 v_2^T v_1 v 1 T X X T v 2 = λ 1 v 1 T v 2 = 0 = v 2 T X X T v 1 = λ 1 v 2 T v 1
最终有主成分组成的矩阵V m × m = [ v 1 , v 2 , . . . , v m ] V_{m \times m } = [v_1,v_2,...,v_m] V m × m = [ v 1 , v 2 , ... , v m ]
Y k × N = V m × k T X m × N Y_{k \times N} = V_{m \times k }^T X_{m \times N} Y k × N = V m × k T X m × N
前面学习了SVD需要求A T A A^TA A T A 1 N − 1 X X T \frac{1}{N-1}XX^T N − 1 1 X X T A = X T N − 1 A = \frac{X^T}{\sqrt{N-1}} A = N − 1 X T X X X X X T XX^T X X T X X T XX^T X X T
稀疏主成分分析 (Sparse PCA )Structured Sparse Principal Component Analysis 以及Online Dictionary Learning for Sparse Coding
( U ∗ , V ∗ ) = arg min U , V 1 2 ∣ ∣ X − U V ∣ ∣ 2 2 + α ∣ ∣ V ∣ ∣ 1 subject to ∣ ∣ U k ∣ ∣ 2 = 1 for all 0 ≤ k < n c o m p o n e n t s \begin{split}(U^*, V^*) = \underset{U, V}{\operatorname{arg\,min\,}} & \frac{1}{2}
||X-UV||_2^2+\alpha||V||_1 \\
\text{subject to } & ||U_k||_2 = 1 \text{ for all }
0 \leq k < n_{components}\end{split} ( U ∗ , V ∗ ) = U , V arg min subject to 2 1 ∣∣ X − U V ∣ ∣ 2 2 + α ∣∣ V ∣ ∣ 1 ∣∣ U k ∣ ∣ 2 = 1 for all 0 ≤ k < n co m p o n e n t s
意思就是求UV让其近似等于X,然后得到一个稀疏矩阵VV V V Matrix decomposition
我们常说的向量(3,2)其实隐式引入了一个定义:以 x 轴和 y 轴上正方向长度为 1 的向量为标准。向量 (3,2) 实际是说在 x 轴投影为 3 而 y 轴的投影为 2。注意投影是一个标量,所以可以为负。
如:另一组基(单位向量)( 1 2 , 1 2 ) (\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}) ( 2 1 , 2 1 ) ( − 1 2 , 1 2 ) (-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}) ( − 2 1 , 2 1 ) a a a 单位向量 x 单位向量x 单位向量 x ⟨ a , x ⟩ = ∥ a ∥ . ∥ x ∥ cos θ = ∥ a ∥ cos θ \braket{a,x} = \|a\|.\|x\|\cos \theta = \|a\|\cos \theta ⟨ a , x ⟩ = ∥ a ∥.∥ x ∥ cos θ = ∥ a ∥ cos θ θ \theta θ
a = ( 3 , 2 ) a=(3,2) a = ( 3 , 2 ) x = ( 1 2 , 1 2 ) x=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}) x = ( 2 1 , 2 1 ) ⟨ a , x ⟩ = 5 2 \braket{a,x} = \frac{5}{\sqrt{2}} ⟨ a , x ⟩ = 2 5 a = ( 3 , 2 ) a=(3,2) a = ( 3 , 2 ) y = ( − 1 2 , 1 2 ) y=(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}) y = ( − 2 1 , 2 1 ) ⟨ a , y ⟩ = − 1 2 \braket{a,y} = -\frac{1}{\sqrt{2}} ⟨ a , y ⟩ = − 2 1
所以新坐标为( 5 2 , − 1 2 ) (\frac{5}{\sqrt{2}},-\frac{1}{\sqrt{2}}) ( 2 5 , − 2 1 )
我们也可以用矩阵来表示(x,y是行向量;a用列向量)[ x y ] [ 3 2 ] = [ 1 2 , 1 2 − 1 2 , 1 2 ] [ 3 2 ] = [ 5 2 − 1 2 ] \begin{bmatrix} x \\ y\end{bmatrix}\begin{bmatrix} 3 \\ 2\end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\end{bmatrix}\begin{bmatrix} 3 \\ 2\end{bmatrix} = \begin{bmatrix} \frac{5}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}}\end{bmatrix} [ x y ] [ 3 2 ] = [ 2 1 , 2 1 − 2 1 , 2 1 ] [ 3 2 ] = [ 2 5 − 2 1 ]
协方差(Covariance )的定义:
cov ( X , Y ) = E [ ( X − E [ X ] ) ( Y − E [ Y ] ) ] cov ( X , Y ) = 1 n ∑ i = 1 n ( x i − E ( X ) ) ( y i − E ( Y ) ) . {\displaystyle \operatorname {cov} (X,Y)=\operatorname {E} {{\big [}(X-\operatorname {E} [X])(Y-\operatorname {E} [Y]){\big ]}}} \\ {\displaystyle \operatorname {cov} (X,Y)={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-E(X))(y_{i}-E(Y)).} cov ( X , Y ) = E [ ( X − E [ X ]) ( Y − E [ Y ]) ] cov ( X , Y ) = n 1 i = 1 ∑ n ( x i − E ( X )) ( y i − E ( Y )) .
性质:cov ( X , Y ) = E [ ( X − E [ X ] ) ( Y − E [ Y ] ) ] = E [ X Y − X E [ Y ] − E [ X ] Y + E [ X ] E [ Y ] ] = E [ X Y ] − E [ X ] E [ Y ] − E [ X ] E [ Y ] + E [ X ] E [ Y ] = E [ X Y ] − E [ X ] E [ Y ] , {\displaystyle {\begin{aligned}\operatorname {cov} (X,Y)&=\operatorname {E} \left[\left(X-\operatorname {E} \left[X\right]\right)\left(Y-\operatorname {E} \left[Y\right]\right)\right]\\&=\operatorname {E} \left[XY-X\operatorname {E} \left[Y\right]-\operatorname {E} \left[X\right]Y+\operatorname {E} \left[X\right]\operatorname {E} \left[Y\right]\right]\\&=\operatorname {E} \left[XY\right]-\operatorname {E} \left[X\right]\operatorname {E} \left[Y\right]-\operatorname {E} \left[X\right]\operatorname {E} \left[Y\right]+\operatorname {E} \left[X\right]\operatorname {E} \left[Y\right]\\&=\operatorname {E} \left[XY\right]-\operatorname {E} \left[X\right]\operatorname {E} \left[Y\right],\end{aligned}}} cov ( X , Y ) = E [ ( X − E [ X ] ) ( Y − E [ Y ] ) ] = E [ X Y − X E [ Y ] − E [ X ] Y + E [ X ] E [ Y ] ] = E [ X Y ] − E [ X ] E [ Y ] − E [ X ] E [ Y ] + E [ X ] E [ Y ] = E [ X Y ] − E [ X ] E [ Y ] ,
cov ( X , a ) = 0 cov ( X , X ) = var ( X ) cov ( X , Y ) = cov ( Y , X ) cov ( a X , b Y ) = a b cov ( X , Y ) cov ( X + a , Y + b ) = cov ( X , Y ) cov ( a X + b Y , c W + d V ) = a c cov ( X , W ) + a d cov ( X , V ) + b c cov ( Y , W ) + b d cov ( Y , V ) {\displaystyle {\begin{aligned}\operatorname {cov} (X,a)&=0\\\operatorname {cov} (X,X)&=\operatorname {var} (X)\\\operatorname {cov} (X,Y)&=\operatorname {cov} (Y,X)\\\operatorname {cov} (aX,bY)&=ab\,\operatorname {cov} (X,Y)\\\operatorname {cov} (X+a,Y+b)&=\operatorname {cov} (X,Y)\\\operatorname {cov} (aX+bY,cW+dV)&=ac\,\operatorname {cov} (X,W)+ad\,\operatorname {cov} (X,V)+bc\,\operatorname {cov} (Y,W)+bd\,\operatorname {cov} (Y,V)\end{aligned}}} cov ( X , a ) cov ( X , X ) cov ( X , Y ) cov ( a X , bY ) cov ( X + a , Y + b ) cov ( a X + bY , c W + d V ) = 0 = var ( X ) = cov ( Y , X ) = ab cov ( X , Y ) = cov ( X , Y ) = a c cov ( X , W ) + a d cov ( X , V ) + b c cov ( Y , W ) + b d cov ( Y , V )
协方差矩阵(Covariance matrix )的定义:对称的方阵 X X X X = ( X 1 , X 2 , . . . , X n ) T {\displaystyle \mathbf {X} =(X_{1},X_{2},...,X_{n})^{\mathrm {T} }} X = ( X 1 , X 2 , ... , X n ) T X X X K X X {\displaystyle \operatorname {K} _{\mathbf {X} \mathbf {X} }} K XX K X i X j = cov [ X i , X j ] = E [ ( X i − E [ X i ] ) ( X j − E [ X j ] ) ] {\displaystyle \operatorname {K} _{X_{i}X_{j}}=\operatorname {cov} [X_{i},X_{j}]=\operatorname {E} [(X_{i}-\operatorname {E} [X_{i}])(X_{j}-\operatorname {E} [X_{j}])]} K X i X j = cov [ X i , X j ] = E [( X i − E [ X i ]) ( X j − E [ X j ])]
K X X = [ E [ ( X 1 − E [ X 1 ] ) ( X 1 − E [ X 1 ] ) ] E [ ( X 1 − E [ X 1 ] ) ( X 2 − E [ X 2 ] ) ] ⋯ E [ ( X 1 − E [ X 1 ] ) ( X n − E [ X n ] ) ] E [ ( X 2 − E [ X 2 ] ) ( X 1 − E [ X 1 ] ) ] E [ ( X 2 − E [ X 2 ] ) ( X 2 − E [ X 2 ] ) ] ⋯ E [ ( X 2 − E [ X 2 ] ) ( X n − E [ X n ] ) ] ⋮ ⋮ ⋱ ⋮ E [ ( X n − E [ X n ] ) ( X 1 − E [ X 1 ] ) ] E [ ( X n − E [ X n ] ) ( X 2 − E [ X 2 ] ) ] ⋯ E [ ( X n − E [ X n ] ) ( X n − E [ X n ] ) ] ] {\displaystyle \operatorname {K} _{\mathbf {X} \mathbf {X} }={\begin{bmatrix}\mathrm {E} [(X_{1}-\operatorname {E} [X_{1}])(X_{1}-\operatorname {E} [X_{1}])]&\mathrm {E} [(X_{1}-\operatorname {E} [X_{1}])(X_{2}-\operatorname {E} [X_{2}])]&\cdots &\mathrm {E} [(X_{1}-\operatorname {E} [X_{1}])(X_{n}-\operatorname {E} [X_{n}])]\\\\\mathrm {E} [(X_{2}-\operatorname {E} [X_{2}])(X_{1}-\operatorname {E} [X_{1}])]&\mathrm {E} [(X_{2}-\operatorname {E} [X_{2}])(X_{2}-\operatorname {E} [X_{2}])]&\cdots &\mathrm {E} [(X_{2}-\operatorname {E} [X_{2}])(X_{n}-\operatorname {E} [X_{n}])]\\\\\vdots &\vdots &\ddots &\vdots \\\\\mathrm {E} [(X_{n}-\operatorname {E} [X_{n}])(X_{1}-\operatorname {E} [X_{1}])]&\mathrm {E} [(X_{n}-\operatorname {E} [X_{n}])(X_{2}-\operatorname {E} [X_{2}])]&\cdots &\mathrm {E} [(X_{n}-\operatorname {E} [X_{n}])(X_{n}-\operatorname {E} [X_{n}])]\end{bmatrix}}} K XX = ⎣ ⎡ E [( X 1 − E [ X 1 ]) ( X 1 − E [ X 1 ])] E [( X 2 − E [ X 2 ]) ( X 1 − E [ X 1 ])] ⋮ E [( X n − E [ X n ]) ( X 1 − E [ X 1 ])] E [( X 1 − E [ X 1 ]) ( X 2 − E [ X 2 ])] E [( X 2 − E [ X 2 ]) ( X 2 − E [ X 2 ])] ⋮ E [( X n − E [ X n ]) ( X 2 − E [ X 2 ])] ⋯ ⋯ ⋱ ⋯ E [( X 1 − E [ X 1 ]) ( X n − E [ X n ])] E [( X 2 − E [ X 2 ]) ( X n − E [ X n ])] ⋮ E [( X n − E [ X n ]) ( X n − E [ X n ])] ⎦ ⎤
样本的协方差 (无偏)c o v ( X , Y ) = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) ( Y i − Y ˉ ) cov(X,Y) = \frac{1}{n - 1}\sum_{i=1}^{n}\left ( X_{i} - \bar{X} \right )\left ( Y_{i} - \bar{Y} \right ) co v ( X , Y ) = n − 1 1 i = 1 ∑ n ( X i − X ˉ ) ( Y i − Y ˉ )
样本的协方差矩阵 :c o v [ X n × p ] n × n = c o v [ X 1 , . . . , X n ] = 1 n − 1 K X X cov[X_{n \times p}]_{n \times n} = cov[X_1,...,X_n] = \frac{1}{n-1}{K} _{\mathbf {X} \mathbf {X} } co v [ X n × p ] n × n = co v [ X 1 , ... , X n ] = n − 1 1 K XX 1 n \frac{1}{n} n 1
np.cov ( X 3 × 2 , r o w v a r = F a l s e ) \text{np.cov}(X_{3 \times 2},rowvar = False) np.cov ( X 3 × 2 , ro w v a r = F a l se ) 2 × 2 2 \times 2 2 × 2 3 × 3 3 \times 3 3 × 3 np.cov ( x , y , z ) \text{np.cov}(x,y,z) np.cov ( x , y , z ) 3 × 3 3 \times 3 3 × 3
期望(Expectation )的定义:E [ X ] = ∑ i = 1 k x i p i = x 1 p 1 + x 2 p 2 + ⋯ + x k p k . p 1 + p 2 + ⋯ + p k = 1 , {\displaystyle \operatorname {E} [X]=\sum _{i=1}^{k}x_{i}\,p_{i}=x_{1}p_{1}+x_{2}p_{2}+\cdots +x_{k}p_{k}.} \\ {\displaystyle p_{1}+p_{2}+\cdots +p_{k}=1,} E [ X ] = i = 1 ∑ k x i p i = x 1 p 1 + x 2 p 2 + ⋯ + x k p k . p 1 + p 2 + ⋯ + p k = 1 ,
性质:E [ X + Y ] = E [ X ] + E [ Y ] , E [ a X ] = a E [ X ] , {\displaystyle {\begin{aligned}\operatorname {E} [X+Y]&=\operatorname {E} [X]+\operatorname {E} [Y],\\\operatorname {E} [aX]&=a\operatorname {E} [X],\end{aligned}}} E [ X + Y ] E [ a X ] = E [ X ] + E [ Y ] , = a E [ X ] ,
如果X , Y X,Y X , Y E [ X Y ] = E [ X ] E [ Y ] {\displaystyle \operatorname {E} [XY]=\operatorname {E} [X]\operatorname {E} [Y]} E [ X Y ] = E [ X ] E [ Y ]
常数的期望等于常数本身E ( a ) = a E(a) = a E ( a ) = a
x i x_i x i X X X X X X x i x_i x i E ( x i ) = E ( X ) , D ( x i ) = D ( X ) E(x_i) = E(X),D(x_i) = D(X) E ( x i ) = E ( X ) , D ( x i ) = D ( X )
E ( X ) E(X) E ( X ) E ( X 2 ) E(X^2) E ( X 2 )
原点矩(raw moment )和中心矩(central moment )E ( X k ) E(X^k) E ( X k ) E ( X − E ( X ) ) k E(X-E(X))^k E ( X − E ( X ) ) k E ( X ) E(X) E ( X )
方差(Variance )的定义:Var ( X ) = E [ ( X − μ ) 2 ] μ = E [ X ] \operatorname {Var} (X)=\operatorname {E} \left[(X-\mu )^{2}\right] \\ {\displaystyle \mu =\operatorname {E} [X]} Var ( X ) = E [ ( X − μ ) 2 ] μ = E [ X ]
性质:D ( X ) D(X) D ( X ) V a r ( X ) Var(X) Va r ( X )
Var ( X ) = Cov ( X , X ) . \operatorname {Var} (X)=\operatorname {Cov} (X,X). Var ( X ) = Cov ( X , X ) . Var ( X ) = E [ ( X − E [ X ] ) 2 ] = E [ X 2 − 2 X E [ X ] + E [ X ] 2 ] = E [ X 2 ] − 2 E [ X ] E [ X ] + E [ X ] 2 = E [ X 2 ] − E [ X ] 2 {\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left[(X-\operatorname {E} [X])^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}-2X\operatorname {E} [X]+\operatorname {E} [X]^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}\right]-2\operatorname {E} [X]\operatorname {E} [X]+\operatorname {E} [X]^{2}\\[4pt]&=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}\end{aligned}}} Var ( X ) = E [ ( X − E [ X ] ) 2 ] = E [ X 2 − 2 X E [ X ] + E [ X ] 2 ] = E [ X 2 ] − 2 E [ X ] E [ X ] + E [ X ] 2 = E [ X 2 ] − E [ X ] 2
Var ( X + Y ) = E [ ( X + Y ) 2 ] − ( E [ X + Y ] ) 2 = E [ X 2 + 2 X Y + Y 2 ] − ( E [ X ] + E [ Y ] ) 2 = E [ X 2 ] + 2 E [ X Y ] + E [ Y 2 ] − ( E [ X ] 2 + 2 E [ X ] E [ Y ] + E [ Y ] 2 ) = E [ X 2 ] + E [ Y 2 ] − E [ X ] 2 − E [ Y ] 2 = Var ( X ) + Var ( Y ) {\displaystyle {\begin{aligned}\operatorname {Var} (X+Y)&=\operatorname {E} \left[(X+Y)^{2}\right]-(\operatorname {E} [X+Y])^{2}\\[5pt]&=\operatorname {E} \left[X^{2}+2XY+Y^{2}\right]-(\operatorname {E} [X]+\operatorname {E} [Y])^{2} \\&=\operatorname {E} \left[X^{2}\right]+2\operatorname {E} [XY]+\operatorname {E} \left[Y^{2}\right]-\left(\operatorname {E} [X]^{2}+2\operatorname {E} [X]\operatorname {E} [Y]+\operatorname {E} [Y]^{2}\right)\\[5pt]&=\operatorname {E} \left[X^{2}\right]+\operatorname {E} \left[Y^{2}\right]-\operatorname {E} [X]^{2}-\operatorname {E} [Y]^{2}\\[5pt]&=\operatorname {Var} (X)+\operatorname {Var} (Y)\end{aligned}}} Var ( X + Y ) = E [ ( X + Y ) 2 ] − ( E [ X + Y ] ) 2 = E [ X 2 + 2 X Y + Y 2 ] − ( E [ X ] + E [ Y ] ) 2 = E [ X 2 ] + 2 E [ X Y ] + E [ Y 2 ] − ( E [ X ] 2 + 2 E [ X ] E [ Y ] + E [ Y ] 2 ) = E [ X 2 ] + E [ Y 2 ] − E [ X ] 2 − E [ Y ] 2 = Var ( X ) + Var ( Y )
Var ( X + a ) = Var ( X ) . \operatorname {Var} (X+a)=\operatorname {Var} (X). Var ( X + a ) = Var ( X ) . Var ( a X ) = a 2 Var ( X ) . \operatorname {Var} (aX)=a^{2}\operatorname {Var} (X). Var ( a X ) = a 2 Var ( X ) . Var ( a X + b Y ) = a 2 Var ( X ) + b 2 Var ( Y ) + 2 a b Cov ( X , Y ) , \operatorname {Var} (aX+bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)+2ab\,\operatorname {Cov} (X,Y), Var ( a X + bY ) = a 2 Var ( X ) + b 2 Var ( Y ) + 2 ab Cov ( X , Y ) , Var ( a X − b Y ) = a 2 Var ( X ) + b 2 Var ( Y ) − 2 a b Cov ( X , Y ) , \operatorname {Var} (aX-bY)=a^{2}\operatorname {Var} (X)+b^{2}\operatorname {Var} (Y)-2ab\,\operatorname {Cov} (X,Y), Var ( a X − bY ) = a 2 Var ( X ) + b 2 Var ( Y ) − 2 ab Cov ( X , Y ) ,
Var ( X Y ) = E ( X 2 ) E ( Y 2 ) − [ E ( X ) ] 2 [ E ( Y ) ] 2 . {\displaystyle \operatorname {Var} (XY)=\operatorname {E} \left(X^{2}\right)\operatorname {E} \left(Y^{2}\right)-[\operatorname {E} (X)]^{2}[\operatorname {E} (Y)]^{2}.} Var ( X Y ) = E ( X 2 ) E ( Y 2 ) − [ E ( X ) ] 2 [ E ( Y ) ] 2 .
参数估计 需要未知参数的估计量和一定置信度偏差 的定义:b i a s ( θ ^ m ) = E ( θ ^ m ) − θ bias(\hat{\theta}_m) = E(\hat{\theta}_m)-\theta bia s ( θ ^ m ) = E ( θ ^ m ) − θ θ \theta θ θ \theta θ θ ^ m \hat{\theta}_m θ ^ m
对估计值的评价标准:
无偏性(Unbiasedness):是估计量(不一定是样本均值)抽样分布的数学期望等与总体参数的真值。m m m b i a s ( θ ^ m ) = 0 bias(\hat{\theta}_m) = 0 bia s ( θ ^ m ) = 0 θ ^ m \hat{\theta}_m θ ^ m 无偏 (unbiased)的,意味着E ( θ ^ m ) = θ E(\hat{\theta}_m) = \theta E ( θ ^ m ) = θ lim m → ∞ b i a s ( θ ^ m ) = 0 \lim_{m \to \infty}bias(\hat{\theta}_m) = 0 lim m → ∞ bia s ( θ ^ m ) = 0 θ ^ m \hat{\theta}_m θ ^ m 渐近无偏 (asymptotically unbiased) 的,意味着 lim m → ∞ E ( θ ^ m ) = θ \lim_{m \to \infty}E(\hat{\theta}_m) = \theta lim m → ∞ E ( θ ^ m ) = θ
有效性(Efficiency):是有时几组数据都是无偏的,但是此时有效数是方差最小的。( x 1 , . . . , x m ) (x_1,...,x_m) ( x 1 , ... , x m ) μ \mu μ σ 2 \sigma^2 σ 2 x i x_i x i E ( x i ) = E ( x 1 ) = . . . = μ E(x_i)=E(x_1)=...=\mu E ( x i ) = E ( x 1 ) = ... = μ D ( x i ) = D ( x 1 ) = . . . = σ 2 D(x_i)=D(x_1)=...=\sigma^2 D ( x i ) = D ( x 1 ) = ... = σ 2 σ 2 \sigma^2 σ 2 x ˉ \bar{x} x ˉ E ( x ˉ ) = E [ 1 m ∑ m x i ] = 1 m E [ ∑ m x i ] = 1 m [ ∑ m E ( x i ) ] = 1 m [ ∑ m μ ] = μ E(\bar{x}) = E[\frac{1}{m}\sum_m x_i] =\frac{1}{m}E[\sum_mx_i] = \frac{1}{m}[\sum_mE(x_i)] = \frac{1}{m}[\sum_m \mu] = \mu E ( x ˉ ) = E [ m 1 ∑ m x i ] = m 1 E [ ∑ m x i ] = m 1 [ ∑ m E ( x i )] = m 1 [ ∑ m μ ] = μ D ( x ˉ ) = D ( 1 m ∑ m x i ) = 1 m 2 D ( ∑ m x i ) = 1 m 2 ∑ m D ( x i ) = 1 m 2 m σ 2 = σ 2 m D(\bar{x}) = D(\frac{1}{m}\sum_m x_i) = \frac{1}{m^2}D(\sum_m x_i) = \frac{1}{m^2}\sum_m D(x_i) = \frac{1}{m^2} m\sigma^2 = \frac{\sigma^2}{m} D ( x ˉ ) = D ( m 1 ∑ m x i ) = m 2 1 D ( ∑ m x i ) = m 2 1 ∑ m D ( x i ) = m 2 1 m σ 2 = m σ 2
一致性(Consistency):是指样本变大,估计越准。lim m → ∞ P ( ∣ θ ^ m − θ ∣ < ϵ ) = 1 \lim_{m \to \infty}P(|\hat{\theta}_m - \theta | \lt \epsilon) = 1 lim m → ∞ P ( ∣ θ ^ m − θ ∣ < ϵ ) = 1
无偏估计 μ ^ = ∑ i = 1 m x i \hat{\mu} = \sum_{i=1}^m x_i μ ^ = ∑ i = 1 m x i μ \mu μ b i a s ( μ ^ ) = E ( μ ^ ) − μ bias(\hat{\mu}) = E(\hat{\mu}) - \mu bia s ( μ ^ ) = E ( μ ^ ) − μ
有偏估计 σ ^ 2 = 1 m ∑ i = 1 m ( x i − μ ^ ) 2 \hat{\sigma}^2 = \frac{1}{m}\sum_{i=1}^m(x_i-\hat{\mu})^2 σ ^ 2 = m 1 ∑ i = 1 m ( x i − μ ^ ) 2 μ ^ = ∑ i = 1 m x i \hat{\mu} = \sum_{i=1}^m x_i μ ^ = ∑ i = 1 m x i b i a s ( σ ^ 2 ) = E [ σ ^ 2 ] − σ 2 bias(\hat{\sigma}^2) = E[\hat{\sigma}^2] - \sigma^2 bia s ( σ ^ 2 ) = E [ σ ^ 2 ] − σ 2 E [ σ ^ 2 ] E[\hat{\sigma}^2] E [ σ ^ 2 ] E [ σ ^ 2 ] = E [ 1 m ∑ i = 1 m ( x i − μ ^ ) 2 ] = E [ 1 m ∑ i = 1 m ( x i 2 − 2 μ ^ x i + μ ^ 2 ) ] = E [ 1 m ∑ i = 1 m x i 2 − 1 m ∑ i = 1 m 2 μ ^ x i + 1 m ∑ i = 1 m μ ^ 2 ] = E [ 1 m ∑ i = 1 m x i 2 − 2 μ ^ 1 m ∑ i = 1 m x i + 1 m ∑ i = 1 m μ ^ 2 ] = E [ 1 m ∑ i = 1 m x i 2 − 2 μ ^ μ ^ + μ ^ 2 ] = E [ 1 m ∑ i = 1 m x i 2 − μ ^ 2 ] = E [ 1 m ∑ i = 1 m x i 2 ] − E [ μ ^ 2 ] = 1 m E [ ∑ i = 1 m x i 2 ] − E [ μ ^ 2 ] E[\hat{\sigma}^2] = E[\frac{1}{m}\sum_{i=1}^m(x_i-\hat{\mu})^2] \\= E[\frac{1}{m}\sum_{i=1}^m(x_i^2- 2\hat{\mu}x_i +\hat{\mu}^2)] \\= E[\frac{1}{m}\sum_{i=1}^mx_i^2-\frac{1}{m}\sum_{i=1}^m 2\hat{\mu}x_i +\frac{1}{m}\sum_{i=1}^m\hat{\mu}^2]\\= E[\frac{1}{m}\sum_{i=1}^mx_i^2-2\hat{\mu}\frac{1}{m}\sum_{i=1}^m x_i +\frac{1}{m}\sum_{i=1}^m\hat{\mu}^2]\\= E[\frac{1}{m}\sum_{i=1}^mx_i^2-2\hat{\mu}\hat{\mu} +\hat{\mu}^2]= E[\frac{1}{m}\sum_{i=1}^mx_i^2-\hat{\mu}^2] \\= E[\frac{1}{m}\sum_{i=1}^mx_i^2]-E[\hat{\mu}^2] = \frac{1}{m}E[\sum_{i=1}^mx_i^2]-E[\hat{\mu}^2] E [ σ ^ 2 ] = E [ m 1 i = 1 ∑ m ( x i − μ ^ ) 2 ] = E [ m 1 i = 1 ∑ m ( x i 2 − 2 μ ^ x i + μ ^ 2 )] = E [ m 1 i = 1 ∑ m x i 2 − m 1 i = 1 ∑ m 2 μ ^ x i + m 1 i = 1 ∑ m μ ^ 2 ] = E [ m 1 i = 1 ∑ m x i 2 − 2 μ ^ m 1 i = 1 ∑ m x i + m 1 i = 1 ∑ m μ ^ 2 ] = E [ m 1 i = 1 ∑ m x i 2 − 2 μ ^ μ ^ + μ ^ 2 ] = E [ m 1 i = 1 ∑ m x i 2 − μ ^ 2 ] = E [ m 1 i = 1 ∑ m x i 2 ] − E [ μ ^ 2 ] = m 1 E [ i = 1 ∑ m x i 2 ] − E [ μ ^ 2 ]
E [ μ ^ 2 ] = D ( μ ^ ) + E ( μ ^ ) 2 E[\hat{\mu}^2] = D(\hat{\mu}) + E(\hat{\mu})^2 E [ μ ^ 2 ] = D ( μ ^ ) + E ( μ ^ ) 2 D ( μ ^ ) = 1 m σ 2 和 E ( μ ^ ) = μ D(\hat{\mu}) = \frac{1}{m} \sigma^2 和 E(\hat{\mu}) = \mu D ( μ ^ ) = m 1 σ 2 和 E ( μ ^ ) = μ E [ μ ^ 2 ] = 1 m σ 2 + μ 2 E[\hat{\mu}^2] = \frac{1}{m} \sigma^2 + \mu^2 E [ μ ^ 2 ] = m 1 σ 2 + μ 2
E [ x i 2 ] = D ( x i ) + E ( x i ) 2 E[{x_i}^2] = D(x_i) + E(x_i)^2 E [ x i 2 ] = D ( x i ) + E ( x i ) 2 D ( x i ) = σ 2 和 E ( x i ) = μ D(x_i) = \sigma^2 和 E(x_i) = \mu D ( x i ) = σ 2 和 E ( x i ) = μ 1 m E [ ∑ i = 1 m x i 2 ] = 1 m ∑ i = 1 m E [ x i 2 ] = σ 2 + μ 2 \frac{1}{m}E[\sum_{i=1}^mx_i^2] = \frac{1}{m}\sum_{i=1}^m E[x_i^2]= \sigma^2 + \mu^2 m 1 E [ ∑ i = 1 m x i 2 ] = m 1 ∑ i = 1 m E [ x i 2 ] = σ 2 + μ 2
所以E [ σ ^ 2 ] = σ 2 + μ 2 − ( 1 m σ 2 + μ 2 ) = m − 1 m σ 2 E[\hat{\sigma}^2] = \sigma^2 + \mu^2 - (\frac{1}{m} \sigma^2 + \mu^2) =\frac{m-1}{m}\sigma^2 E [ σ ^ 2 ] = σ 2 + μ 2 − ( m 1 σ 2 + μ 2 ) = m m − 1 σ 2
所以方差的无偏估计为σ ~ 2 = 1 m − 1 ∑ i = 1 m ( x i − μ ^ ) 2 \tilde{\sigma}^2 = \frac{1}{m-1}\sum_{i=1}^m(x_i-\hat{\mu})^2 σ ~ 2 = m − 1 1 ∑ i = 1 m ( x i − μ ^ ) 2
当lim m → ∞ 1 m ∑ i = 1 m ( x i − μ ^ ) 2 = 1 m − 1 ∑ i = 1 m ( x i − μ ^ ) 2 \lim_{m \to \infty}\frac{1}{m}\sum_{i=1}^m(x_i-\hat{\mu})^2 = \frac{1}{m-1}\sum_{i=1}^m(x_i-\hat{\mu})^2 lim m → ∞ m 1 ∑ i = 1 m ( x i − μ ^ ) 2 = m − 1 1 ∑ i = 1 m ( x i − μ ^ ) 2
无偏估计不一定是最好的估计!
因子分析(Factor analysis, FA )
每个变量都可以表示成公共因子的线性函数与特殊因子之和X i = a i 1 F 1 + a i 2 F 2 + . . . + + a i m F m + ϵ i , ( i = 1 , 2 , . . . , p ) X_i = a_{i1}F_1 + a_{i2}F_2 +...++ a_{im}F_m + \epsilon_i ,(i=1,2,...,p) X i = a i 1 F 1 + a i 2 F 2 + ... + + a im F m + ϵ i , ( i = 1 , 2 , ... , p ) X = AF+εX = [ X 1 , X 2 . . . X p ] T X = [X_1,X_2...X_p]^T X = [ X 1 , X 2 ... X p ] T A = [ a 11 a 12 . . . a 1 m a 21 a 22 . . . a 2 m . . . . . . . . . . . . a p 1 a p 2 . . . a p m ] A= \begin{bmatrix}
a_{11} & a_{12} & ... & a_{1m} \\\\
a_{21} & a_{22} & ... & a_{2m} \\\\
... & ... & ... & ... \\\\
a_{p1} & a_{p2} & ... & a_{pm} \\\\
\end{bmatrix} A = ⎣ ⎡ a 11 a 21 ... a p 1 a 12 a 22 ... a p 2 ... ... ... ... a 1 m a 2 m ... a p m ⎦ ⎤ F = [ F 1 , F 2 . . . F m ] T F = [F_1,F_2...F_m]^T F = [ F 1 , F 2 ... F m ] T ϵ = [ ϵ 1 , ϵ 2 . . . ϵ p ] T \epsilon = [\epsilon_1,\epsilon_2...\epsilon_p]^T ϵ = [ ϵ 1 , ϵ 2 ... ϵ p ] T
主成分分析,是分析维度属性的主要成分表示。
独立成分分析(Independent component analysis, ICA )
X=ASY=WX=WAS , A = inv(W)
ICA是找出构成信号的相互独立部分(不需要正交),对应高阶统计量分析。ICA理论认为用来观测的混合数据阵X是由独立元S经过A线性加权获得。
独立成分分析 (ICA) 应用参考(Origin来做ICA分析)
独立成分分析 - 讲解的原理
Independent Component Analysis (ICA)
[16-1] 方开泰. 实用多元统计分析. 上海:华东师范大学出版社, 1989.
我们先介绍下文本信息处理中的一些问题:
一词多义(多义现象)polysemy
一义多词(同义现象)synonymy
LSA能解决同义(语义相似度)问题:发现单词与主题之间的关系,这里主题是汽车;也能解决一定程度的多义问题,同一个单词在不同文档中表示不同话题
潜在语义分析(Latent semantic analysis, LSA )旨在 解决这种方法不能准确表示语义的问题,试图从大量的文本数据中发现潜在的话题,以话题向量表示文本的语义内容,以话题向量空间的度量更准确地表示文本之间的语义相似度。
文本doc集合D = { d 1 , d 2 , . . . , d n } D = \{d_1,d_2,...,d_n\} D = { d 1 , d 2 , ... , d n } W = { w 1 , w 2 , . . . , w m } W = \{w_1,w_2,...,w_m\} W = { w 1 , w 2 , ... , w m } X = [ x 11 x 12 ⋯ x 1 n x 21 x 22 ⋯ x 2 n ⋮ ⋮ ⋮ x m 1 x m 2 ⋯ x m n ] X = \begin{bmatrix}
x_{11} & x_{12} & \cdots & x_{1n} \\
x_{21} & x_{22} & \cdots & x_{2n} \\
\vdots & \vdots & & \vdots \\
x_{m1} & x_{m2} & \cdots & x_{mn} \\
\end{bmatrix} X = ⎣ ⎡ x 11 x 21 ⋮ x m 1 x 12 x 22 ⋮ x m 2 ⋯ ⋯ ⋯ x 1 n x 2 n ⋮ x mn ⎦ ⎤ x i j x_{ij} x ij w i w_i w i d j d_j d j
权值通常用单词频率-逆文档频率 (term frequency–inverse document frequency,TFIDF )表示,定义为:tf-idf ( t , d , D ) = t f ( t , d ) ⋅ i d f ( t , D ) {\displaystyle \text {tf-idf} (t,d,D)=\mathrm {tf} (t,d)\cdot \mathrm {idf} (t,D)} tf-idf ( t , d , D ) = tf ( t , d ) ⋅ idf ( t , D ) x i j = tf-idf ( w i , d j , D ) x_{ij} = \text {tf-idf} (w_i,d_j,D) x ij = tf-idf ( w i , d j , D ) N = ∣ D ∣ N = |D| N = ∣ D ∣ t f ( t , d ) = f t , d ∑ t ′ ∈ d f t ′ , d = t 在 d 中出现的频数 d 中出现的所有单词的频数和 {\displaystyle \mathrm {tf} (t,d)={\frac {f_{t,d}}{\sum _{t'\in d}{f_{t',d}}}} = \frac{t在d中出现的频数}{d中出现的所有单词的频数和}} tf ( t , d ) = ∑ t ′ ∈ d f t ′ , d f t , d = d 中出现的所有单词的频数和 t 在 d 中出现的频数 i d f ( t , D ) = log N ∣ { d ∈ D : t ∈ d } ∣ = log 文档总数 含有单词 t 的文本总数 \mathrm{idf}(t, D) = \log \frac{N}{|\{d \in D: t \in d\}| } = \log \frac{文档总数}{含有单词t的文本总数} idf ( t , D ) = log ∣ { d ∈ D : t ∈ d } ∣ N = log 含有单词 t 的文本总数 文档总数
直观上理解:
相似度(余弦相似度) (Cosine similarity )可以表示两个文本之间的语义相似度,越大越相似。A ⋅ B = ∥ A ∥ ∥ B ∥ cos θ {\displaystyle \mathbf {A} \cdot \mathbf {B} =\left\|\mathbf {A} \right\|\left\|\mathbf {B} \right\|\cos \theta } A ⋅ B = ∥ A ∥ ∥ B ∥ cos θ similarity = cos ( θ ) = A ⋅ B ∥ A ∥ ∥ B ∥ = ∑ i = 1 n A i B i ∑ i = 1 n A i 2 ∑ i = 1 n B i 2 , {\displaystyle {\text{similarity}}=\cos(\theta )={\mathbf {A} \cdot \mathbf {B} \over \|\mathbf {A} \|\|\mathbf {B} \|}={\frac {\sum \limits _{i=1}^{n}{A_{i}B_{i}}}{{\sqrt {\sum \limits _{i=1}^{n}{A_{i}^{2}}}}{\sqrt {\sum \limits _{i=1}^{n}{B_{i}^{2}}}}}},} similarity = cos ( θ ) = ∥ A ∥∥ B ∥ A ⋅ B = i = 1 ∑ n A i 2 i = 1 ∑ n B i 2 i = 1 ∑ n A i B i ,
文档用向量表示:d i = x . i = [ x 1 i x 2 i ⋮ x m i ] d_i = x_{.i} = \begin{bmatrix} x_{1i} \\ x_{2i} \\ \vdots \\ x_{mi} \end{bmatrix} d i = x . i = ⎣ ⎡ x 1 i x 2 i ⋮ x mi ⎦ ⎤ d i , d j d_i,d_j d i , d j similarity = x . i ⋅ x . j ∥ x . i ∥ ∥ x . j ∥ \text{similarity} = \frac{x_{.i}\cdot x_{.j}}{\|x_{.i}\|\|x_{.j}\|} similarity = ∥ x . i ∥∥ x . j ∥ x . i ⋅ x . j 单词向量空间 (word vector space model)中,有一个问题就是多义和同义现象,这时我们就可以考虑话题向量空间 (topic vector space model):
单词-文本矩阵X = [ x 11 x 12 ⋯ x 1 n x 21 x 22 ⋯ x 2 n ⋮ ⋮ ⋮ x m 1 x m 2 ⋯ x m n ] X = \begin{bmatrix}
x_{11} & x_{12} & \cdots & x_{1n} \\
x_{21} & x_{22} & \cdots & x_{2n} \\
\vdots & \vdots & & \vdots \\
x_{m1} & x_{m2} & \cdots & x_{mn} \\
\end{bmatrix} X = ⎣ ⎡ x 11 x 21 ⋮ x m 1 x 12 x 22 ⋮ x m 2 ⋯ ⋯ ⋯ x 1 n x 2 n ⋮ x mn ⎦ ⎤ T T T T = [ t 11 t 12 ⋯ t 1 k t 21 t 22 ⋯ t 2 k ⋮ ⋮ ⋮ t m 1 t m 2 ⋯ t m k ] T = \begin{bmatrix}
t_{11} & t_{12} & \cdots & t_{1k} \\
t_{21} & t_{22} & \cdots & t_{2k} \\
\vdots & \vdots & & \vdots \\
t_{m1} & t_{m2} & \cdots & t_{mk} \\
\end{bmatrix} T = ⎣ ⎡ t 11 t 21 ⋮ t m 1 t 12 t 22 ⋮ t m 2 ⋯ ⋯ ⋯ t 1 k t 2 k ⋮ t mk ⎦ ⎤
那么文档在话题向量空间的表示(话题-文本矩阵)Y = [ y 11 y 12 ⋯ y 1 n y 21 y 22 ⋯ y 2 n ⋮ ⋮ ⋮ y k 1 y k 2 ⋯ y k n ] Y = \begin{bmatrix}
y_{11} & y_{12} & \cdots & y_{1n} \\
y_{21} & y_{22} & \cdots & y_{2n} \\
\vdots & \vdots & & \vdots \\
y_{k1} & y_{k2} & \cdots & y_{kn} \\
\end{bmatrix} Y = ⎣ ⎡ y 11 y 21 ⋮ y k 1 y 12 y 22 ⋮ y k 2 ⋯ ⋯ ⋯ y 1 n y 2 n ⋮ y kn ⎦ ⎤
模型 :X m × n ≈ T m × k Y k × n X_{m \times n} \approx T_{m \times k}Y_{k \times n} X m × n ≈ T m × k Y k × n X m × n X_{m \times n} X m × n T m × k T_{m \times k} T m × k Y k × n Y_{k \times n} Y k × n 就是我们想要的输出 ;策略 :m i n i m i z e ∥ X − T Y ∥ 2 minimize \|X - TY\|^2 minimi ze ∥ X − T Y ∥ 2 算法 :X m × n ≈ X r a n k ( k ) = U m × k Σ k × k V n × k T X_{m \times n} \approx X_{rank(k)} = U_{m \times k}\Sigma_{k \times k} V^T_{n \times k} X m × n ≈ X r ank ( k ) = U m × k Σ k × k V n × k T T = U k T=U_k T = U k Y = Σ k V k T Y = \Sigma_kV_k^T Y = Σ k V k T X ≈ W H X \approx WH X ≈ W H T = W T=W T = W Y = H Y = H Y = H
[17-1] Deerwester S C, Dumais S T, Landauer T K, et al. Indexing by latent semantic analysis. Journal of the Association for Information Science and Technology ,1990, 41: 391-407.Learning the parts of objects by non-negative matrix factorization . Nature, 1999, 401(6755):788-791.SIGIR Conference in Research and Development in Information Retrieval , 2003.SIGIR Conference in Research and Development in Information Retrieval , 2011.
生成模型,用隐变量表示话题
概率潜在语义分析(Probabilistic latent semantic analysis, PLSA )
概率有向图模型:
模型 :W = { w 1 , . . . , w M } W = \{w_1,...,w_M\} W = { w 1 , ... , w M } D = { d 1 , . . . , d N } D=\{d_1,...,d_N\} D = { d 1 , ... , d N } Z = { z 1 , . . . , z K } Z=\{z_1,...,z_K\} Z = { z 1 , ... , z K } P ( w , d ) = P ( d ) P ( w ∣ d ) = P ( d ) ∑ z P ( w , z ∣ d ) = P ( d ) ∑ z P ( z ∣ d ) P ( w ∣ z ) P(w,d) =P(d)P(w|d) = P(d)\sum_{z} P(w,z|d)=P(d)\sum _{z}P(z|d)P(w|z) P ( w , d ) = P ( d ) P ( w ∣ d ) = P ( d ) z ∑ P ( w , z ∣ d ) = P ( d ) z ∑ P ( z ∣ d ) P ( w ∣ z ) P ( w , z ∣ d ) = P ( z ∣ d ) P ( w ∣ z , d ) = P ( z ∣ d ) P ( w ∣ z ) P(w,z|d) = P(z|d)P(w|z,d) = P(z|d)P(w|z) P ( w , z ∣ d ) = P ( z ∣ d ) P ( w ∣ z , d ) = P ( z ∣ d ) P ( w ∣ z ) w ⊥ d ∣ z w \perp d |z w ⊥ d ∣ z P ( w , d ) P(w,d) P ( w , d )
依据概率分布P(d),从文本集合中随机选取一个文本d,共生成N个文本;针对每个文本,执行下一步操作
在文本d给定条件下,依据条件概率分布P(z|d),从话题集合中随机选取一个话题z,共生成L个话题,这里L是文本长度(每个话题生成一个单词,所以生成的文本d的长度是L)
在话题z给定条件下,依据概率分布P(w|z),从单词集合中随机选取一个单词w
文本-单词共现数据(矩阵T)的生成概率为所有单词-文本对(w,d)的生成概率乘积,P ( T ) = ∏ ( w , d ) P ( w , d ) n ( w , d ) T = [ n ( w i , d j ) ] i = 1 , 2 , . . . , M ; j = 1 , 2 , . . . , N P(T) = \prod_{(w,d)} P(w,d)^{n(w,d)} \\ T = [n(w_i,d_j)] i=1,2,...,M; j=1,2,...,N P ( T ) = ( w , d ) ∏ P ( w , d ) n ( w , d ) T = [ n ( w i , d j )] i = 1 , 2 , ... , M ; j = 1 , 2 , ... , N n ( w , d ) n(w,d) n ( w , d ) n ( w , d ) n(w,d) n ( w , d )
这里假设文本的长度都是等长的,正常情况是第一个文本的长度是L1,...,第N个文本的长度是LN;∑ i = 1 N L i \sum_{i=1}^N L_i ∑ i = 1 N L i
书中还讲到了等价的共现模型(对称模型) P ( w , d ) = ∑ z P ( z ) P ( d ∣ z ) P ( w ∣ z ) P(w,d)=\sum _{z}P(z)P(d|z)P(w|z) P ( w , d ) = z ∑ P ( z ) P ( d ∣ z ) P ( w ∣ z )
策略 :L = log P ( T ) = log ∏ i = 1 M ∏ j = 1 N P ( w i , d j ) n ( w i , d j ) = ∑ i = 1 M ∑ j = 1 N n ( w i , d j ) log P ( w i , d j ) = ∑ i = 1 M ∑ j = 1 N n ( w i , d j ) [ log P ( d ) + log ∑ k = 1 K P ( w i ∣ z k ) P ( z k ∣ d j ) ] L =\log P(T) = \log \prod_{i=1}^{M} \prod_{j=1}^{N} {P\left(w_{i}, d_{j}\right)}^{n\left(w_{i}, d_{j}\right) } \\=\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log P\left(w_{i}, d_{j}\right) \\ =\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \left[\log P(d)+\log \sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right] L = log P ( T ) = log i = 1 ∏ M j = 1 ∏ N P ( w i , d j ) n ( w i , d j ) = i = 1 ∑ M j = 1 ∑ N n ( w i , d j ) log P ( w i , d j ) = i = 1 ∑ M j = 1 ∑ N n ( w i , d j ) [ log P ( d ) + log k = 1 ∑ K P ( w i ∣ z k ) P ( z k ∣ d j ) ] L = ∑ i = 1 M ∑ j = 1 N n ( w i , d j ) log [ ∑ k = 1 K P ( w i ∣ z k ) P ( z k ∣ d j ) ] L =\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log \left[ \sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right] L = i = 1 ∑ M j = 1 ∑ N n ( w i , d j ) log [ k = 1 ∑ K P ( w i ∣ z k ) P ( z k ∣ d j ) ] arg max θ L ( θ ) = arg max θ ∑ i = 1 M ∑ j = 1 N n ( w i , d j ) log [ ∑ k = 1 K P ( w i ∣ z k ) P ( z k ∣ d j ) ] \arg \max _{\theta} L(\theta)=\arg \max _{\theta} \sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log \left[ \sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right) \right] arg θ max L ( θ ) = arg θ max i = 1 ∑ M j = 1 ∑ N n ( w i , d j ) log [ k = 1 ∑ K P ( w i ∣ z k ) P ( z k ∣ d j ) ]
算法 :
现在进行E步,计算Q函数arg max θ L ( θ ) = arg max θ ∑ i = 1 M ∑ j = 1 N n ( w i , d j ) log ∑ k = 1 K P ( z k ∣ w i , d j ) P ( w i ∣ z k ) P ( z k ∣ d j ) P ( z k ∣ w i , d j ) \arg \max _{\theta} L(\theta)=\arg \max _{\theta} \sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log \sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right) \frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)} arg θ max L ( θ ) = arg θ max i = 1 ∑ M j = 1 ∑ N n ( w i , d j ) log k = 1 ∑ K P ( z k ∣ w i , d j ) P ( z k ∣ w i , d j ) P ( w i ∣ z k ) P ( z k ∣ d j ) E z [ P ( w i ∣ z k ) P ( z k ∣ d j ) P ( z k ∣ w i , d j ) ] = ∑ k = 1 K P ( z k ∣ w i , d j ) P ( w i ∣ z k ) P ( z k ∣ d j ) P ( z k ∣ w i , d j ) E_z \left[\frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\right] = \sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right) \frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)} E z [ P ( z k ∣ w i , d j ) P ( w i ∣ z k ) P ( z k ∣ d j ) ] = k = 1 ∑ K P ( z k ∣ w i , d j ) P ( z k ∣ w i , d j ) P ( w i ∣ z k ) P ( z k ∣ d j ) arg max θ L ( θ ) = arg max θ ∑ i = 1 M ∑ j = 1 N n ( w i , d j ) log E z [ P ( w i ∣ z k ) P ( z k ∣ d j ) P ( z k ∣ w i , d j ) ] \arg \max _{\theta} L(\theta)=\arg \max _{\theta} \sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \log E_z \left[\frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\right] arg θ max L ( θ ) = arg θ max i = 1 ∑ M j = 1 ∑ N n ( w i , d j ) log E z [ P ( z k ∣ w i , d j ) P ( w i ∣ z k ) P ( z k ∣ d j ) ] log E z [ P ( w i ∣ z k ) P ( z k ∣ d j ) P ( z k ∣ w i , d j ) ] ≥ E z [ log P ( w i ∣ z k ) P ( z k ∣ d j ) P ( z k ∣ w i , d j ) ] \log E_{z}\left[\frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\right] \geq E_{z}\left[\log \frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\right] log E z [ P ( z k ∣ w i , d j ) P ( w i ∣ z k ) P ( z k ∣ d j ) ] ≥ E z [ log P ( z k ∣ w i , d j ) P ( w i ∣ z k ) P ( z k ∣ d j ) ] ∑ i = 1 M ∑ j = 1 N n ( w i , d j ) E z [ log P ( w i ∣ z k ) P ( z k ∣ d j ) P ( z k ∣ w i , d j ) ] = ∑ i = 1 M ∑ j = 1 N n ( w i , d j ) ∑ k = 1 K P ( z k ∣ w i , d j ) [ log P ( w i ∣ z k ) P ( z k ∣ d j ) − log P ( z k ∣ w i , d j ) ] \sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) E_z \left[\log \frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{P\left(z_{k} \mid w_{i}, d_{j}\right)}\right] \\ =\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right)\left[\log P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)-\log P\left(z_{k} \mid w_{i}, d_{j}\right)\right] i = 1 ∑ M j = 1 ∑ N n ( w i , d j ) E z [ log P ( z k ∣ w i , d j ) P ( w i ∣ z k ) P ( z k ∣ d j ) ] = i = 1 ∑ M j = 1 ∑ N n ( w i , d j ) k = 1 ∑ K P ( z k ∣ w i , d j ) [ log P ( w i ∣ z k ) P ( z k ∣ d j ) − log P ( z k ∣ w i , d j ) ] ∑ k = 1 K P ( z k ∣ w i , d j ) log P ( z k ∣ w i , d j ) \sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right) \log P\left(z_{k} \mid w_{i}, d_{j}\right) ∑ k = 1 K P ( z k ∣ w i , d j ) log P ( z k ∣ w i , d j ) Q = ∑ i = 1 M ∑ j = 1 N n ( w i , d j ) ∑ k = 1 K P ( z k ∣ w i , d j ) log [ P ( w i ∣ z k ) P ( z k ∣ d j ) ] Q=\sum_{i=1}^{M} \sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) \sum_{k=1}^{K} P\left(z_{k} \mid w_{i}, d_{j}\right) \log \left[P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)\right] Q = i = 1 ∑ M j = 1 ∑ N n ( w i , d j ) k = 1 ∑ K P ( z k ∣ w i , d j ) log [ P ( w i ∣ z k ) P ( z k ∣ d j ) ] P ( z k ∣ w i , d j ) , P ( w i ∣ z k ) , P ( z k ∣ d j ) P\left(z_{k} \mid w_{i}, d_{j}\right),P\left(w_{i} \mid z_{k}\right), P\left(z_{k} \mid d_{j}\right) P ( z k ∣ w i , d j ) , P ( w i ∣ z k ) , P ( z k ∣ d j ) P ( z k ∣ w i , d j ) = P ( w i ∣ z k ) P ( z k ∣ d j ) ∑ k = 1 K P ( w i ∣ z k ) P ( z k ∣ d j ) P\left(z_{k} \mid w_{i}, d_{j}\right)=\frac{P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)}{\sum_{k=1}^{K} P\left(w_{i} \mid z_{k}\right) P\left(z_{k} \mid d_{j}\right)} P ( z k ∣ w i , d j ) = ∑ k = 1 K P ( w i ∣ z k ) P ( z k ∣ d j ) P ( w i ∣ z k ) P ( z k ∣ d j )
M步P ( w i ∣ z k ) , P ( z k ∣ d j ) P\left(w_{i} \mid z_{k}\right), P\left(z_{k} \mid d_{j}\right) P ( w i ∣ z k ) , P ( z k ∣ d j ) P ( z k ∣ w i , d j ) P\left(z_{k} \mid w_{i}, d_{j}\right) P ( z k ∣ w i , d j ) max Q s . t . ∑ i = 1 M P ( w i ∣ z k ) = 1 , k = 1 , 2 , ⋯ , K ∑ k = 1 K P ( z k ∣ d j ) = 1 , j = 1 , 2 , ⋯ , N \max Q \\s.t. \quad \begin{array}{l}\sum_{i=1}^{M} P\left(w_{i} \mid z_{k}\right)=1, \quad k=1,2, \cdots, K \\ \sum_{k=1}^{K} P\left(z_{k} \mid d_{j}\right)=1, \quad j=1,2, \cdots, N\end{array} max Q s . t . ∑ i = 1 M P ( w i ∣ z k ) = 1 , k = 1 , 2 , ⋯ , K ∑ k = 1 K P ( z k ∣ d j ) = 1 , j = 1 , 2 , ⋯ , N Λ = Q ′ + ∑ k = 1 K τ k ( 1 − ∑ i = 1 M P ( w i ∣ z k ) ) + ∑ j = 1 N ρ j ( 1 − ∑ k = 1 K P ( z k ∣ d j ) ) \Lambda=Q^{\prime}+\sum_{k=1}^{K} \tau_{k}\left(1-\sum_{i=1}^{M} P\left(w_{i} \mid z_{k}\right)\right)+\sum_{j=1}^{N} \rho_{j}\left(1-\sum_{k=1}^{K} P\left(z_{k} \mid d_{j}\right)\right) Λ = Q ′ + k = 1 ∑ K τ k ( 1 − i = 1 ∑ M P ( w i ∣ z k ) ) + j = 1 ∑ N ρ j ( 1 − k = 1 ∑ K P ( z k ∣ d j ) ) P ( w i ∣ z k ) , P ( z k ∣ d j ) P\left(w_{i} \mid z_{k}\right), P\left(z_{k} \mid d_{j}\right) P ( w i ∣ z k ) , P ( z k ∣ d j ) ∑ j = 1 N n ( w i , d j ) P ( z k ∣ w i , d j ) − τ k P ( w i ∣ z k ) = 0 , i = 1 , 2 , ⋯ , M ; k = 1 , 2 , ⋯ , K ∑ i = 1 M n ( w i , d j ) P ( z k ∣ w i , d j ) − ρ j P ( z k ∣ d j ) = 0 , j = 1 , 2 , ⋯ , N ; k = 1 , 2 , ⋯ , K \begin{array}{l}\sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)-\tau_{k} P\left(w_{i} \mid z_{k}\right)=0, \quad i=1,2, \cdots, M ; \quad k=1,2, \cdots, K \\ \sum_{i=1}^{M} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)-\rho_{j} P\left(z_{k} \mid d_{j}\right)=0, \quad j=1,2, \cdots, N ; \quad k=1,2, \cdots, K\end{array} ∑ j = 1 N n ( w i , d j ) P ( z k ∣ w i , d j ) − τ k P ( w i ∣ z k ) = 0 , i = 1 , 2 , ⋯ , M ; k = 1 , 2 , ⋯ , K ∑ i = 1 M n ( w i , d j ) P ( z k ∣ w i , d j ) − ρ j P ( z k ∣ d j ) = 0 , j = 1 , 2 , ⋯ , N ; k = 1 , 2 , ⋯ , K P ( w i ∣ z k ) = ∑ j = 1 N n ( w i , d j ) P ( z k ∣ w i , d j ) ∑ m = 1 M ∑ j = 1 N n ( w m , d j ) P ( z k ∣ w m , d j ) P\left(w_{i} \mid z_{k}\right)=\frac{\sum_{j=1}^{N} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)}{\sum_{m=1}^{M} \sum_{j=1}^{N} n\left(w_{m}, d_{j}\right) P\left(z_{k} \mid w_{m}, d_{j}\right)} P ( w i ∣ z k ) = ∑ m = 1 M ∑ j = 1 N n ( w m , d j ) P ( z k ∣ w m , d j ) ∑ j = 1 N n ( w i , d j ) P ( z k ∣ w i , d j ) P ( z k ∣ d j ) = ∑ i = 1 M n ( w i , d j ) P ( z k ∣ w i , d j ) n ( d j ) P\left(z_{k} \mid d_{j}\right)=\frac{\sum_{i=1}^{M} n\left(w_{i}, d_{j}\right) P\left(z_{k} \mid w_{i}, d_{j}\right)}{n\left(d_{j}\right)} P ( z k ∣ d j ) = n ( d j ) ∑ i = 1 M n ( w i , d j ) P ( z k ∣ w i , d j ) n ( d j ) = ∑ i = 1 M n ( w i , d j ) n(d_j) = \sum_{i=1}^M n(w_i,d_j) n ( d j ) = ∑ i = 1 M n ( w i , d j ) d j d_j d j n ( w i , d j ) n(w_i,d_j) n ( w i , d j ) w i w_i w i d j d_j d j
[18-1] Hofmann T. Probabilistic Latent Semantic analysis. Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence, 1999: 289-296.Probabilistic Latent Semantic Indexing . Proceedings of the 22nd Annual International ACM SIGIR Conference in Research and Development in Information Retrieval , 1999.Unsupervised learning by probabilistic latent semantic analysis . Machine Learning, 2001, 42: 177-196.
马尔可夫链蒙特卡罗 (Markov Chain Monte Carlo, MCMC )由两个MC组成,即蒙特卡罗方法 (Monte Carlo Simulation, MC )和马尔可夫链 (Markov Chain, MC )。
要弄懂MCMC的原理我们首先得搞清楚蒙特卡罗方法和马尔可夫链的原理。
马尔可夫链在前面的章节有讲到,再结合书中的内容。这里补充下几个知识:马尔可夫链的遍历定理 :
可逆马尔可夫链 (reversible Markov chain):X = { X 0 , X 1 , . . . , X t , . . . } X=\{X_0,X_1,...,X_t,...\} X = { X 0 , X 1 , ... , X t , ... } π = ( π 1 , π 2 , . . . ) T \pi = (\pi_1,\pi_2,...)^T π = ( π 1 , π 2 , ... ) T i , j ∈ S i,j \in S i , j ∈ S P ( X t = i ∣ X t − 1 = j ) π j = P ( X t − 1 = j ∣ X t = i ) π i , i , j = 1 , 2 , . . . P(X_t=i|X_{t-1}=j)\pi_j = P(X_{t-1}=j|X_t=i)\pi_i ,\quad i,j =1,2,... P ( X t = i ∣ X t − 1 = j ) π j = P ( X t − 1 = j ∣ X t = i ) π i , i , j = 1 , 2 , ... p i j π j = p j i π i , i , j = 1 , 2 , . . . p_{ij}\pi_j = p_{ji}\pi_i ,\quad i,j =1,2,... p ij π j = p ji π i , i , j = 1 , 2 , ... 细致平衡方程 (detailed balance equation),并且满足细致平衡方程的状态分布π \pi π
采样法 (Sampling Method )也称为蒙特卡罗方法(Monte Carlo Method, MC )或统计模拟方法(Statistical Simulation Method)
蒙特卡罗方法诞生于20 世纪 40 年代美国的“曼哈顿计划”,其名字来源于摩纳哥的一个以赌博业闻名的城市蒙特卡罗,象征概率.数值解 (Numerical solution与其对应的是闭式解Closed-form solution或解析解Analytical solution)的方法.
最早的蒙特卡罗方法都是为了求解一些不太好求解的求和或者积分问题。比如积分:θ = ∫ a b f ( x ) d x \theta = \int_a^b f(x)dx θ = ∫ a b f ( x ) d x π \pi π
我们可以通过蒙特卡罗方法来模拟求解近似值。如何模拟呢?
随机采样 指从给定概率密度函数 𝑝(𝑥) 中抽取出符合其概率分布的样本.
随机采样 采样法的难点是如何进行随机采样,即如何让计算机生成满足概率密度函数 𝑝(𝑥) 的样本.我们知道,计算机可以比较容易地随机生成一个在 [0, 1]区间上均布分布的样本 𝜉.如果要随机生成服从某个非均匀分布的样本,就需要一些间接的采样方法.c d f − 1 ( 𝑦 ) , 𝑦 ∈ [ 0 , 1 ] cdf^{−1}(𝑦), 𝑦 ∈ [0, 1] c d f −1 ( y ) , y ∈ [ 0 , 1 ] 累积分布函数的逆函数 (inverse CDF)来生成服从该随机分布的样本.假设 𝜉 是 [0, 1] 区间上均匀分布的随机变量,则 c d f − 1 ( ξ ) cdf^{−1}(\xi) c d f −1 ( ξ ) 拒绝采样、重要性采样、马尔可夫链蒙特卡罗采样 等.这些方法一般是先根据一个比较容易采样的分布进行采样,然后通过一些策略来间接得到符合𝑝(𝑥)分布的样本.
rejection sampling, inverse CDF, Box-Muller, Ziggurat algorithm
拒绝采样 (Rejection Sampling)是一种间接采样方法,也称为接受-拒绝采样(Acceptance-Rejection Sampling).x ˆ \^{x} x ˆ α ( x ˆ ) = p ( x ˆ ) k q ( x ˆ ) \alpha(\^{x}) = \frac{p(\^{x})}{kq(\^{x})} α ( x ˆ ) = k q ( x ˆ ) p ( x ˆ ) α ( x ˆ ) \alpha(\^{x}) α ( x ˆ ) x ˆ \^{x} x ˆ
拒绝采样的采样过程
输入: 提议分布𝑞(𝑥),常数𝑘,样本集合𝒱 = ∅;
1 repeat
2 根据𝑞(𝑥)随机生成一个样本 ;̂𝑥
3 计算接受概率𝛼( ̂𝑥);
4 从(0, 1)的均匀分布中随机生成一个值𝑧;
5 if 𝑧 ≤ 𝛼( ̂𝑥) then // 以𝛼(𝑥)̂ 的概率接受𝒙̂
6 𝒱 = 𝒱 ∪ { ̂𝑥};
7 end
8 until 获得 𝑁 个样本(|𝒱| = 𝑁);
输出: 样本集合𝒱
判断一个拒绝采样方法的好坏就是看其采样效率,即总体的接受率.如果函数𝑘𝑞(𝑥)远大于原始分布函数 ̂𝑝(𝑥),拒绝率会比较高,采样效率会非常不理想.但要找到一个和 ̂𝑝(𝑥)比较接近的提议分布往往比较困难.特别是在高维空间中,其采样率会非常低,导致很难应用到实际问题中.
重要性采样 (Importance sampling)E p [ f ( x ) ] = ∫ x f ( x ) p ( x ) d x = ∫ x f ( x ) p ( x ) q ( x ) q ( x ) d x = ∫ x f ( x ) w ( x ) q ( x ) d x = E q [ f ( x ) w ( x ) ] E_p[f(x)] = \int_x f(x)p(x)dx = \int_x f(x)\frac{p(x)}{q(x)}q(x)dx = \int_x f(x)w(x)q(x)dx = E_q[f(x)w(x)] E p [ f ( x )] = ∫ x f ( x ) p ( x ) d x = ∫ x f ( x ) q ( x ) p ( x ) q ( x ) d x = ∫ x f ( x ) w ( x ) q ( x ) d x = E q [ f ( x ) w ( x )]
重要性采样(Importance Sampling)是通过引入重要性权重,将分布 𝑝(𝑥)下𝑓(𝑥)的期望变为在分布𝑞(𝑥)下𝑓(𝑥)𝑤(𝑥)的期望,从而可以近似为E p [ f ( x ) ] = E q [ f ( x ) w ( x ) ] = 1 N ∑ i = 1 N f ( x i ) w ( x i ) = 1 N ∑ i = 1 N f ( x i ) p ( x i ) q ( x i ) E_p[f(x)] = E_q[f(x)w(x)] =\frac{1}{N} \sum_{i=1}^N f(x_i)w(x_i) =\frac{1}{N} \sum_{i=1}^N f(x_i)\frac{p(x_i)}{q(x_i)} E p [ f ( x )] = E q [ f ( x ) w ( x )] = N